Integrator-based Filters

We can convert passive RLC filters into integrator-based active filters in a systematic way using signal flow graphs.

Signal Flow Graphs

Signal flow graphs (SFGs) are topological representations of electrical circuits with two components: (1) nodes, and (2) branches. Any network that can be described by a set of linear differential equations can be represented by a SFG. In a SFG, the nodes represent the variables, e.g. voltages or currents, and the branches represent transfer functions between these node variables, specified by branch multiplication factors (BMFs). These BMFs are obtained from Kirchhoff's equations (KVL and KCL). Note that the branches are directed, as indicated by the arrows. Figs. 1-3 shows a few examples of SFG nodes and branches.

Figure 1: A general impedance where 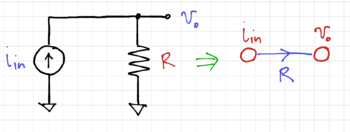$v_{o}=Z\cdot i_{\text{in}}$.	Figure 2: A resistor where $v_{o}=R\cdot i_{\text{in}}$.
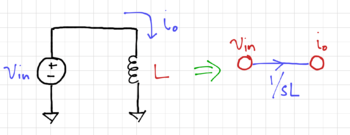Figure 3: An inductor where $i_{o}={\tfrac {1}{sL}}\cdot v_{\text{in}}$.

Useful SFG Properties

We can use the following properties to transform signal flow graphs into forms that can allow us to convert passive RLC filters into its active integrator-based counterparts.

Figure 4: Parallel branches.

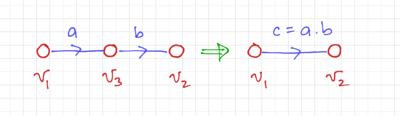Figure 5: Series branches and node absorption.

Parallel Branches

For two or more parallel branches between two nodes in the same direction, as seen in Fig. 4, the effective branch multiplication factor becomes:

$v_{2}=a\cdot v_{1}=b\cdot v_{1}=\left(a+b\right)\cdot v_{1}=c\cdot v_{1}$

(1)

Node Absorption

We can also remove intermediate nodes as shown in Fig. 5:

${\begin{aligned}v_{3}&=a\cdot v_{1}\\v_{2}&=b\cdot v_{3}=\left(a\cdot b\right)\cdot v_{1}=c\cdot v_{1}\end{aligned}}$

(2)

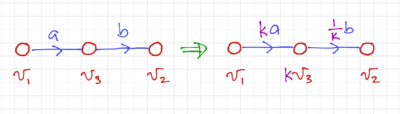Figure 6: Node and branch scaling.

Figure 7: Loops in signal flow graphs.

Branch Scaling

Node values in Fig. 6 can be scaled by a factor $k$, but with the corresponding changes on the incoming and outgoing branch:

${\begin{aligned}v_{3}=a\cdot v_{1}&\rightarrow k\cdot v_{3}=\left(k\cdot a\right)\cdot v_{1}\\v_{2}=b\cdot v_{3}&\rightarrow v_{2}={\frac {b}{k}}\cdot \left(k\cdot v_{3}\right)\end{aligned}}$

(3)

Loops

For the loop shown in Fig. 7, we get:

${\begin{aligned}v_{3}&=a\cdot v_{2}-b\cdot v_{3}\\&={\frac {a}{1+b}}\cdot v_{2}\end{aligned}}$

(4)

Example: A First-Order Low-Pass Filter

Consider the RC filter shown in Fig. 8. To convert this passive filter into its active equivalent, we can go through the following steps:

Figure 8: A passive RC filter.

Step 1: Name all the voltages and current

All the component voltages and currents are named, as seen in Fig. 8.

Step 2: Use KCL/KVL to obtain the integrator forms

We can get the integrator forms of the reactive components by writing the capacitor voltages as:

$v_{\text{capacitor}}=f\left(i_{\text{capacitor}}\right)={\frac {1}{C}}\int i_{\text{capacitor}}\cdot dt\rightarrow {\frac {1}{sC}}\cdot i_{\text{capacitor}}$

(5)

And the inductor currents as:

$i_{\text{inductor}}=f\left(v_{\text{inductor}}\right)={\frac {1}{L}}\int v_{\text{inductor}}\cdot dt\rightarrow {\frac {1}{sL}}\cdot v_{\text{inductor}}$

(6)

Thus, for the simple RC filter, we can write out the voltages as:

${\begin{aligned}v_{1}&=v_{i}-v_{C}\\v_{C}&=i_{2}\cdot {\frac {1}{sC}}\\v_{o}&=v_{C}\end{aligned}}$

(7)

And the currents as:

${\begin{aligned}i_{1}&=v_{1}\cdot {\frac {1}{R_{s}}}\\i_{2}&=i_{1}\end{aligned}}$

(8)

Step 3: Construct the SFG

To systematically construct the signal flow graph, let us create the voltage nodes on the top row, and below them, their corresponding current nodes, as shown in Fig. 9. We can then add the branches, starting with the capacitor branch in its integrator form. We then get one possible SFG (Fig. 9).

Figure 9: The signal flow graph from KCL and KVL equations.

Step 4: Normalization

The normalization step converts all the current nodes into voltage nodes using a scaling resistance, $R^{*}$, as shown in Fig. 10, converting $i_{1}$ and $i_{2}$ into $v_{1}^{\prime }=R^{*}\cdot i_{1}$ and $v_{2}^{\prime }=R^{*}\cdot i_{2}$.

Figure 10: The normalized signal flow graph.

We can then simplify the SFG by combining nodes $v_{C}$ and $v_{o}$ as seen in Fig. 11, and by choosing $R^{*}=R$. We then get the SFG in Fig. 12.

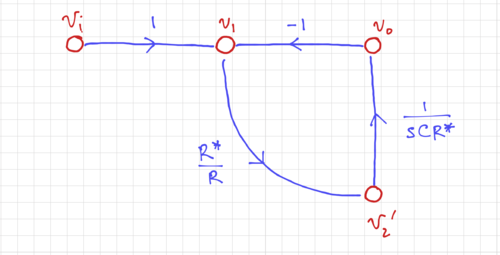Figure 11: The simplified signal flow graph.

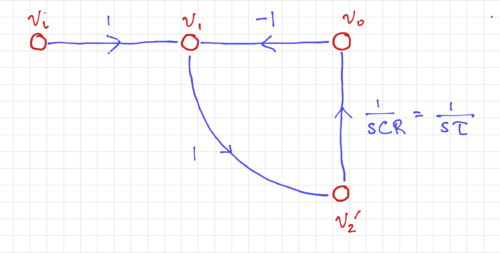Figure 12: The signal flow graph with $R^{*}=R$.

We then convert the SFG into its integrator-based equivalent, as shown in Fig. 13. By inverting the input, i.e. multiplying the input by $-1$ (Fig. 14), and moving the summation into a two-input integrator (Fig. 15), we can easily match this structure to a 2-input op-amp-based integrator (which is presented here), as shown in Fig. 16.

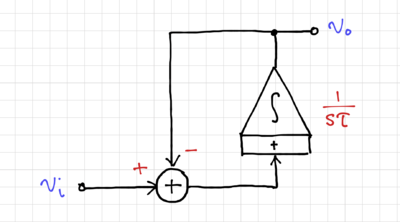Figure 13: The integrator-based equivalent active filter.	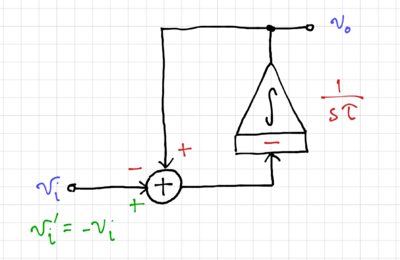Figure 14: Inverting the input to match an inverting integrator.
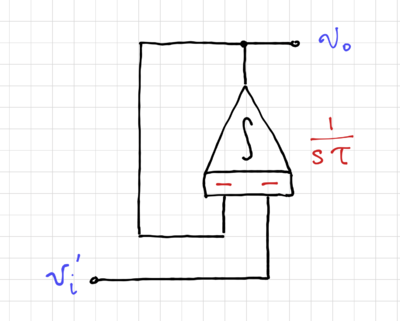Figure 15: Moving the summation into the integrator.	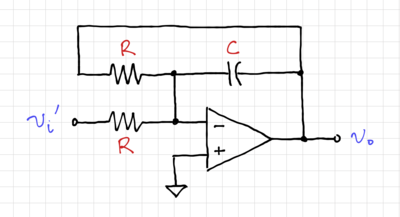Figure 16: The active filter using operational amplifiers.

The transfer function, as expected, is equal to:

${\frac {v_{o}}{v_{i}^{\prime }}}=-{\frac {1}{1+s\tau }}=-{\frac {1}{1+sRC}}$

(9)

We can also calculate the total integrated output noise (as derived here):

${\overline {v_{o,{\text{T}}}^{2}}}={\frac {2kT}{C}}$

(10)