Filter Basics
Filtering is the oldest and most common type of signal processing, usually in the form of frequency selectivity or phase shaping, or both. Some filter applications include (1) extracting a desired signal from other signals, (2) separating signals from noise, (3) anti-aliasing in analog-to-digital converters or smoothing in digital-to-analog converters, (4) phase equalization, and (5) limiting amplifier bandwidths for reducing noise.
Contents
Filter Types
As shown in Figs. 1-5, we can classify filters based on frequency range selectivity as: (1) low-pass filters, (2) high-pass filters, (3) band-pass filters, (4) band-stop, band-reject, or notch filters, and (5) all-pass filters used for phase shaping or equalization.
Note that we can easily derive high-pass and band-pass filters from their low-pass equivalents, and thus, even though most of our examples feature low-pass filters, the concepts and ideas are applicable to the other filter types.
Ideal vs. Practical Filters
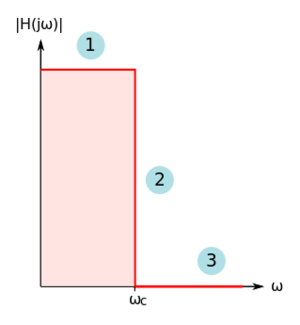
Let us consider an ideal low-pass filter, whose magnitude response is shown in Fig. 6. This ideal filter response has three properties: (1) it has a flat magnitude in the pass-band, resulting in no amplitude distortion in the signals we are passing, (2) it has a "brick wall" transition region, i.e. the transition between the pass-band and stop-band is abrupt, and (3) it has infinite rejection of out-of-band signals, i.e. zero magnitude response. These characteristics make building an ideal filter rather impractical.
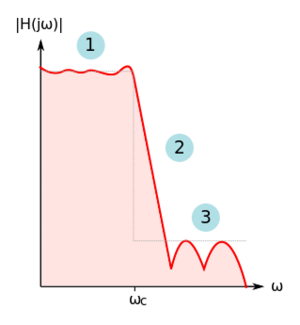
A real filter has the following magnitude response properties, as shown in Fig. 7:
- The pass-band could contain ripples, thus causing amplitude distortion in the signals being passed by the filter.
- There is a finite transition region between the pass-band and the stop-band.
- The rejection of stop-band (or out-of-band) signals is finite.
Magnitude and Frequency Metrics
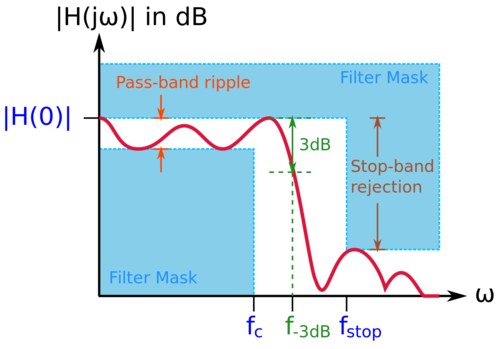
In the design of filters, we can specify the filter specifications using following parameters, as illustrated in Fig. 8:
- DC Pass-band Gain,
- The value of the magnitude transfer function at DC or as .
- Corner Frequency,
- The corner frequency specification.
- Stop-band Frequency,
- The stop-band frequency specification.
The frequency range from to is the transition region separating the pass-band from the stop-band. Instead of individual separate metrics, another way of detailing the filter specifications is by using filter mask, also shown in Fig. 8. The filter mask is a graphical representation of the allowable values the filter magnitude response can take.