Integrators

The Ideal Integrator

The ideal integrator, shown in Fig. 1, with symbol shown in Fig. 2, makes use of an ideal operational amplifier with $A_{v}\rightarrow \infty$, $R_{i}\rightarrow \infty$, and $R_{o}=0$.

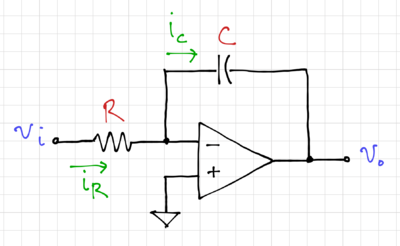Figure 1: The op-amp-based ideal integrator.

Figure 2: The symbol for an integrator.

The current through the resistor, $i_{R}$, can be expressed as:

$i_{R}={\frac {v_{i}}{R}}=i_{C}=-C\cdot {\frac {\partial v_{o}}{\partial t}}$

(1)

Thus, we can write the integrator output voltage, $v_{o}$, as:

$v_{o}=-{\frac {1}{RC}}\int v_{i}\cdot dt$

(2)

In the Laplace domain:

${\frac {v_{i}\left(s\right)}{R}}=-sC\cdot v_{o}\left(s\right)$

(3)

Or equivalently:

$H\left(s\right)={\frac {v_{o}\left(s\right)}{v_{i}\left(s\right)}}=-{\frac {1}{s\cdot RC}}=-{\frac {1}{s\cdot \tau }}=-{\frac {\omega _{0}}{s}}$

(4)

The magnitude and phase response of an ideal integrator is shown in Figs. 3 and 4. A key feature to note in ideal integrators is the fact that:

• The unity gain frequency is equal to $\omega _{0}$, and
• The phase at the unity gain frequency is exactly $-90^{\circ }$.

Figure 3: Magnitude response of an ideal integrator with $\omega _{0}=1\,\mathrm {\tfrac {rad}{s}}$.

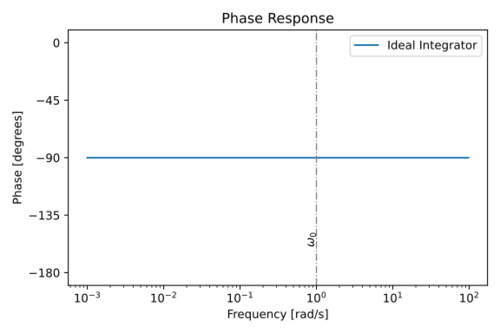Figure 4: Phase response of an ideal integrator with $\omega _{0}=1\,\mathrm {\tfrac {rad}{s}}$.

Rewriting the transfer function as:

$H\left(s\right)=H\left(j\omega \right)=-{\frac {\omega _{0}}{j\omega }}={\frac {1}{-j{\frac {\omega }{\omega _{0}}}}}={\frac {1}{R\left(\omega \right)+jX\left(\omega \right)}}$

(5)

We can then define the quality factor of an ideal integrator:

$Q={\frac {X\left(\omega \right)}{R\left(\omega \right)}}\rightarrow \infty$

(6)

Since $R\left(\omega \right)=0$. Fig. 5 shows a multiple-input integrator, with output voltage:

$v_{o}\left(s\right)=-{\frac {1}{s\cdot R_{1}C}}\cdot v_{1}\left(s\right)-{\frac {1}{s\cdot R_{2}C}}\cdot v_{2}\left(s\right)$

(7)

Integrator Noise

Fig. 6 shows an integrator where the output is fed back to one of its inputs, giving us:

$v_{o}\left(s\right)=-{\frac {1}{s\cdot R_{1}C}}\cdot v_{i}\left(s\right)-{\frac {1}{s\cdot R_{2}C}}\cdot v_{o}\left(s\right)$

(8)

Ignoring the noise from the amplifier, the output noise of the integrator in Fig. 6 can be expressed as:

${\begin{aligned}{\frac {\overline {v_{o}^{2}}}{\Delta f}}&=\left|H_{1}\left(s\right)\right|^{2}\cdot {\frac {\overline {v_{n1}^{2}}}{\Delta f}}+\left|H_{2}\left(s\right)\right|^{2}\cdot {\frac {\overline {v_{n2}^{2}}}{\Delta f}}\\&=\left|{\frac {1}{1+sR_{1}C}}\right|^{2}\cdot {\frac {\overline {v_{n1}^{2}}}{\Delta f}}+\left|{\frac {1}{1+sR_{2}C}}\right|^{2}\cdot {\frac {\overline {v_{n2}^{2}}}{\Delta f}}\\&={\frac {1}{1+\omega ^{2}R_{1}^{2}C^{2}}}\cdot {\frac {\overline {v_{n1}^{2}}}{\Delta f}}+{\frac {1}{1+\omega ^{2}R_{2}^{2}C^{2}}}\cdot {\frac {\overline {v_{n2}^{2}}}{\Delta f}}\\&={\frac {1}{1+\omega ^{2}R_{1}^{2}C^{2}}}\cdot 4kTR_{1}+{\frac {1}{1+\omega ^{2}R_{2}^{2}C^{2}}}\cdot 4kTR_{2}\\\end{aligned}}$

(9)

The total integrated noise is then:

${\begin{aligned}{\overline {v_{o,{\text{T}}}^{2}}}&=\int _{0}^{\infty }\left|H_{1}\left(s\right)\right|^{2}\cdot {\frac {\overline {v_{n1}^{2}}}{\Delta f}}\cdot df+\int _{0}^{\infty }\left|H_{2}\left(s\right)\right|^{2}\cdot {\frac {\overline {v_{n2}^{2}}}{\Delta f}}\cdot df\\&=\int _{0}^{\infty }{\frac {1}{1+\omega ^{2}R_{1}^{2}C^{2}}}\cdot 4kTR_{1}\cdot df+\int _{0}^{\infty }{\frac {1}{1+\omega ^{2}R_{2}^{2}C^{2}}}\cdot 4kTR_{2}\cdot df\\&={\frac {kT}{C}}+{\frac {kT}{C}}={\frac {2kT}{C}}\\\end{aligned}}$

(10)

Integrator Non-Idealities

In practice, integrators are limited by the characteristics of non-ideal amplifiers: (1) finite gain at DC, and (2) non-dominant amplifier poles. Let us look at the effects of these non-idealities one at a time.

Finite Gain

The transfer function of an integrator using an amplifier with finite gain, $a$, can be written as:

$H\left(s\right)={\frac {a}{1+s{\frac {a}{\omega _{0}}}}}={\frac {1}{{\frac {1}{a}}+j{\frac {\omega }{\omega _{0}}}}}$

(11)

The magnitude and phase response of this non-ideal integrator is shown in Figs. 7 and 8.

Figure 7: The magnitude response of an integrator with a finite-gain amplifier.

Figure 8: The phase response of an integrator with a finite-gain amplifier.

Note that the integrator quality factor now becomes finite:

$Q={\frac {\omega }{\omega _{0}}}\cdot a$

(12)

The phase at $\omega =\omega _{0}$ is then:

$\angle \left.H\left(s\right)\right|_{\omega =\omega _{0}}=-\tan ^{-1}\left.\left({\frac {\omega }{\omega _{0}}}\cdot a\right)\right|_{\omega =\omega _{0}}=-\tan ^{-1}a$

(13)

Thus, if $a$ is finite, $\angle \left.H\left(s\right)\right|_{\omega =\omega _{0}}$ will approach, but will never be equal to $-90^{\circ }$, resulting in a phase lead. For example, if $a=100$, we get $\angle \left.H\left(s\right)\right|_{\omega =\omega _{0}}=-89.427^{\circ }$, and $a=1\times 10^{6}$ will result in $\angle \left.H\left(s\right)\right|_{\omega =\omega _{0}}=-89.999427^{\circ }$.

Non-Dominant Poles

The transfer function of an integrator using an amplifier with infinite gain but with non-dominant poles can be expressed as:

$H\left(s\right)={\frac {1}{{\frac {s}{\omega _{0}}}\cdot \left(1+{\frac {s}{p_{2}}}\right)\cdot \left(1+{\frac {s}{p_{3}}}\right)\cdots }}$

(14)

The magnitude and phase response of this non-ideal integrator is shown in Figs. 9 and 10.

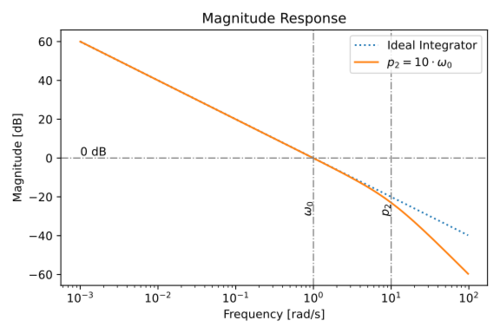Figure 9: The magnitude response of an integrating using an amplifier with a non-dominant pole, $p_{2}$.

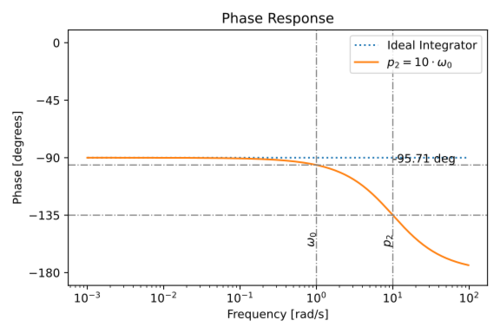Figure 10: The phase response of an integrating using an amplifier with a non-dominant pole, $p_{2}$.

The phase at the unity gain frequency is then equal to:

$\angle \left.H\left(s\right)\right|_{\omega =\omega _{0}}=-90-\tan ^{-1}\left({\frac {\omega _{0}}{p_{2}}}\right)-\tan ^{-1}\left({\frac {\omega _{0}}{p_{3}}}\right)-\ldots$

(15)

Note that the non-dominant poles contribute to the integrator phase lag.

In a real integrator, the effects (phase lead) of the amplifier finite gain can cancel out the effects (phase lag) of the non-dominant poles! Given the transfer function of the integrator with an amplifier that has both finite gain and non-dominant poles:

$H\left(s\right)={\frac {a}{\left(1+s{\frac {a}{\omega _{0}}}\right)\cdot \left(1+{\frac {s}{p_{2}}}\right)\cdot \left(1+{\frac {s}{p_{3}}}\right)\cdots }}$

(16)

If we assume that $\omega _{0}\ll p_{2},p_{3},\ldots$ and $a\gg 1$, we can then rewrite the transfer function as:

${\begin{aligned}\left.H\left(j\omega \right)\right|_{\omega =\omega _{0}}&={\frac {1}{\left({\frac {1}{a}}+{\frac {j\omega _{0}}{\omega _{0}}}\right)\cdot \left(1+{\frac {j\omega _{0}}{p_{2}}}\right)\cdot \left(1+{\frac {j\omega _{0}}{p_{3}}}\right)+\cdots }}\\&={\frac {1}{\left({\frac {1}{a}}-{\frac {\omega _{0}}{p_{2}}}+j+{\frac {j\omega _{0}}{a\cdot p_{2}}}\right)\cdot \left(1+{\frac {j\omega _{0}}{p_{3}}}\right)+\cdots }}\approx {\frac {1}{\left({\frac {1}{a}}-{\frac {\omega _{0}}{p_{2}}}+j\right)\cdot \left(1+{\frac {j\omega _{0}}{p_{3}}}\right)+\cdots }}\\&\approx {\frac {1}{\left({\frac {1}{a}}-{\frac {\omega _{0}}{p_{2}}}+j+{\frac {j\omega _{0}}{a\cdot p_{3}}}-{\frac {j\omega _{0}^{2}}{p_{2}\cdot p_{3}}}-{\frac {\omega _{0}}{p_{3}}}\right)\cdots }}\approx {\frac {1}{\left({\frac {1}{a}}-{\frac {\omega _{0}}{p_{2}}}-{\frac {\omega _{0}}{p_{3}}}+j\right)\cdots }}\\&\approx {\frac {1}{\left({\frac {1}{a}}-{\frac {\omega _{0}}{p_{2}}}-{\frac {\omega _{0}}{p_{3}}}-\ldots \right)+j}}\\&\approx {\frac {1}{\left({\frac {1}{a}}-\sum \limits _{i=2}^{N}{\frac {\omega _{0}}{p_{i}}}\right)+j}}\end{aligned}}$

(17)

For $N$ non-dominant poles. The integrator quality factor is then equal to:

$Q\approx {\frac {1}{{\frac {1}{a}}-\sum \limits _{i=2}^{N}{\frac {\omega _{0}}{p_{i}}}}}$

(18)

As expected, the effect of finite gain can be cancelled out by the effect of the non-dominant poles.

Capacitor Non-Idealities

For lossy capacitors, modeled in Fig. 11 as an ideal capacitor in series with a resistor, $R_{c}$, the integrator transfer function becomes:

${\begin{aligned}H\left(s\right)={\frac {v_{o}}{v_{i}}}&=-\left(R_{c}+{\frac {1}{sC}}\right)\cdot {\frac {1}{R}}=-{\frac {1}{sRC}}\cdot \left(1+sR_{c}C\right)\\&=-{\frac {\omega _{0}}{s}}\cdot \left(1+sR_{c}C\right)=-{\frac {\omega _{0}}{j\omega }}\cdot \left(1+j\omega R_{c}C\right)\\&=-{\frac {\omega _{0}}{j\omega }}\cdot {\frac {1+\omega ^{2}R_{c}^{2}C^{2}}{1-j\omega R_{c}C}}\end{aligned}}$

(19)

The magnitude and phase response is shown in Figs. 12 and 13. Notice the phase lead introduced by the zero due to $R_{c}$. At $\omega =\omega _{0}$:

${\begin{aligned}H\left(j\omega _{0}\right)&=-{\frac {1}{j}}\cdot {\frac {1+\omega _{0}^{2}R_{c}^{2}C^{2}}{1-j\omega _{0}R_{c}C}}={\frac {-\left(1+\omega _{0}^{2}R_{c}^{2}C^{2}\right)}{j+\omega _{0}R_{c}C}}\\&={\frac {-1}{j{\frac {1}{1+\omega _{0}^{2}R_{c}^{2}C^{2}}}+{\frac {\omega _{0}R_{c}C}{1+\omega _{0}^{2}R_{c}^{2}C^{2}}}}}\end{aligned}}$

(20)

The integrator quality factor can then be written as:

$Q={\frac {1}{\omega _{0}R_{c}C}}={\frac {RC}{R_{c}C}}={\frac {R}{R_{c}}}$

(21)

Thus, a non-zero $R_{c}$ degrades the integrator quality factor, but in typical implementations, the amplifier non-idealities will dominate.

Summary

The quality factor of the integrator is reduced by:

• The finite gain of the amplifier,
• The presence of amplifier non-dominant poles, and
• The loss of passive reactive components, e.g. capacitors.

Note that both the finite amplifier gain and the lossy capacitor introduces a phase lead, and the presence of non-dominant poles results in a phase lag.