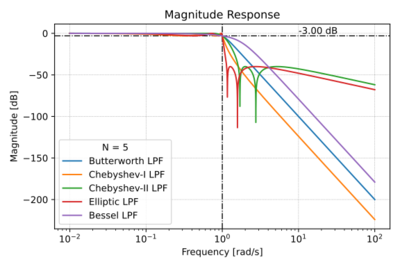
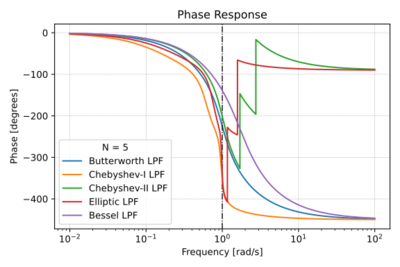
Filter Families
The location of the poles and zeros of a filter transfer function determines both the magnitude and phase response of that filter. Thus, one important filter metric is the filter order, which specifies the order of the polynomial in the denominator of the transfer function, i.e. the number of poles. Let us look at several filter families, where each family has a particular scheme for pole and zero placement, resulting in certain unique characteristics. Though there are other filter families, we will focus on these four families: (1) Butterworth Filters, (2) Chebyshev Filters, (3) Elliptic Filters, and (4) Bessel Filters.
We will start with low-pass filters, but we can easily convert low-pass filters to their high-pass and band-pass counterparts, with the same characteristics as their low-pass equivalents.
Figs. 1-4 show a quick summary of the characteristics of the four filter families listed above.