Difference between revisions of "CoE 197U Power and Energy"
| Line 11: | Line 11: | ||
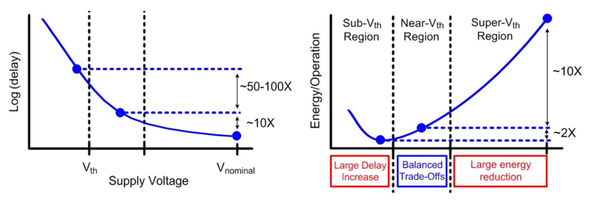
By reducing the supply voltage, the speed will also be degraded. Shown in Fig. 1 (left) is an illustration of the relationship between supply voltage and speed (delay). Note that the y-axis is in log scale and therefore a linear plot (in semilog) is what we expect. However, notice also that the rate of increase in delay (and therefore decease in speed) increases as we reduce the supply voltage. Looking at the energy per operation (right), we can see that the energy per operation is minimum at some point and starts to increase again at V<sub>DD</sub> < V<sub>th</sub> due to the very large delay. Here we can see the advantage of lowering VDD to near threshold (otherwise called near-threshold computing, or NTC). At this voltage, energy consumption is low (though not the minimum achievable) and a slight variation in voltage may increase or decrease energy but only by a small amount. | By reducing the supply voltage, the speed will also be degraded. Shown in Fig. 1 (left) is an illustration of the relationship between supply voltage and speed (delay). Note that the y-axis is in log scale and therefore a linear plot (in semilog) is what we expect. However, notice also that the rate of increase in delay (and therefore decease in speed) increases as we reduce the supply voltage. Looking at the energy per operation (right), we can see that the energy per operation is minimum at some point and starts to increase again at V<sub>DD</sub> < V<sub>th</sub> due to the very large delay. Here we can see the advantage of lowering VDD to near threshold (otherwise called near-threshold computing, or NTC). At this voltage, energy consumption is low (though not the minimum achievable) and a slight variation in voltage may increase or decrease energy but only by a small amount. | ||
| + | |||
| + | [[File:Fig1-ntc.png|center|thumb|600px|Fig. 1. Near-threshold Computing<ref name="dreslinski2010">R. G. Dreslinski, M. Wieckowski, D. Blaauw, D. Sylvester, and T. Mudge, '''Near-Threshold Computing: Reclaiming Moore’s Law Through Energy Efficient Integrated Circuits''', Proc. IEEE, vol. 98, no. 2, pp. 253–266, Feb. 2010</ref>]] | ||
In terms of node transition, aside from actual signal activity, signal statistics for different gates could also help in estimating the effect on power and energy. See slides 7-9 for this. | In terms of node transition, aside from actual signal activity, signal statistics for different gates could also help in estimating the effect on power and energy. See slides 7-9 for this. | ||
Revision as of 19:46, 23 March 2021
In this lecture, we will cover the following topics:
- Power and Energy
- Energy Efficient Techniques
- Metrics
Use the provided slide deck to guide you through this discussion. The main reference for this lecture is Chapter 5 of the Digital IC book[1] and Chapter 4 of the Enabling the IoT book[2].
Power
Power consumption can be classified into dynamic power and static power. Majority of the power consumption comes from the switching of signals, or what we call dynamic power. Static power comes from leakage currents, or the current through the devices when they are supposed to be OFF. Dynamic power comes from the switching of signals, or the charging and discharging of capacitive loads. It can be computed as CLVDD2f, where CL is the capacitive load being charged/discharged, VDD is the supply voltage and f is the frequency of transition. Considering that majority of the power comes from dynamic power, and based on the above equation, we can then say that reducing the supply voltage would be the best choice to reduce power (due to the square relation of power and supply voltage). Other possible ways to reduce power is by reducing switching activity (effectively f) and/or reduce capacitance (CL).
By reducing the supply voltage, the speed will also be degraded. Shown in Fig. 1 (left) is an illustration of the relationship between supply voltage and speed (delay). Note that the y-axis is in log scale and therefore a linear plot (in semilog) is what we expect. However, notice also that the rate of increase in delay (and therefore decease in speed) increases as we reduce the supply voltage. Looking at the energy per operation (right), we can see that the energy per operation is minimum at some point and starts to increase again at VDD < Vth due to the very large delay. Here we can see the advantage of lowering VDD to near threshold (otherwise called near-threshold computing, or NTC). At this voltage, energy consumption is low (though not the minimum achievable) and a slight variation in voltage may increase or decrease energy but only by a small amount.
In terms of node transition, aside from actual signal activity, signal statistics for different gates could also help in estimating the effect on power and energy. See slides 7-9 for this.
Metrics
Considering that changing some parameters (e.g., supply voltage) affects more than one characteristic (e.g., power and speed), it is important to define the metric/s to be used to characterize or evaluate the system. The power-delay product (PDP) is one possible metric which has been used for some time. Energy-delay product (EDP) is another metric we can use. In Fig. 2 on the left, we can see how the energy consumption of 3 different microprocessors – unpipelined, pipelined and super-scalar. This, however, is an expected since unpipelined processors are very simple while super-scalar processors are built for speed and performance. Looking at the energy-delay product as a metric (Fig. 2 right), therefore, we can see that the super-scalar implementation has the lowest EDP and the unpipelined having more twice the EDP of super-scalar.
We can generalize these metrics for energy-delay trade-off as EnDm, wherein the higher n is compared to m, the more we are prioritizing energy consumption and vice versa (the higher m is compared to n, the more we are prioritizing speed). Fig. 3 shows an energy-efficient curve (EEC), which defines the minimum EnDm value.
References
- ↑ J. Rabaey, A. Chandrakasan, B. Nikolic, Digital Integrated Circuits, 2nd ed., 2002
- ↑ M. Alioto, ed., Enabling the Internet of Things from Integrated Circuits to Integrated Systems, Springer International Publishing, 2017
- ↑ R. G. Dreslinski, M. Wieckowski, D. Blaauw, D. Sylvester, and T. Mudge, Near-Threshold Computing: Reclaiming Moore’s Law Through Energy Efficient Integrated Circuits, Proc. IEEE, vol. 98, no. 2, pp. 253–266, Feb. 2010