Difference between revisions of "Butterworth Filters"
Jump to navigation
Jump to search
| Line 1: | Line 1: | ||
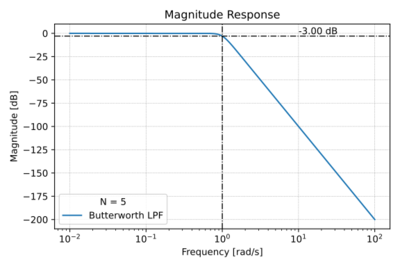
| + | [[File:Butterworth mag.svg|thumb|400px|Figure 1: The Butterworth low-pass filter with <math>N=5</math>.]] | ||
| + | |||
Butterworth filters are a class of ''all-pole filters'', where the poles of the normalized transfer function are equally spaced along the unit circle (<math>\omega_0 = 1\,\text{rad/s}</math>). This results in a '''maximally flat''' pass-band magnitude response, or equivalently: | Butterworth filters are a class of ''all-pole filters'', where the poles of the normalized transfer function are equally spaced along the unit circle (<math>\omega_0 = 1\,\text{rad/s}</math>). This results in a '''maximally flat''' pass-band magnitude response, or equivalently: | ||
Revision as of 17:23, 15 March 2021
Butterworth filters are a class of all-pole filters, where the poles of the normalized transfer function are equally spaced along the unit circle (). This results in a maximally flat pass-band magnitude response, or equivalently:
-
(1)
-
This means that the derivative of the magnitude at DC is zero.
The Low-Pass Butterworth Filter
The low-pass Butterworth filter has the following magnitude response:
-
(2)
-
Where is the filter order and is the frequency. Note that at . Thus:
-
(3)
-
Thus, the poles are the roots of:
-
(4)
-
Or equivalently:
-
(5)
-
Since we can write , the roots of can be written as:
-
(6)
-
For . Thus, we get:
-
(7)
-
Solving for , we get the poles of the low-pass Butterworth filter:
-
(8)
-
We can then write:
-
(9)
-