Difference between revisions of "CoE 197U Logical Effort"
| Line 15: | Line 15: | ||
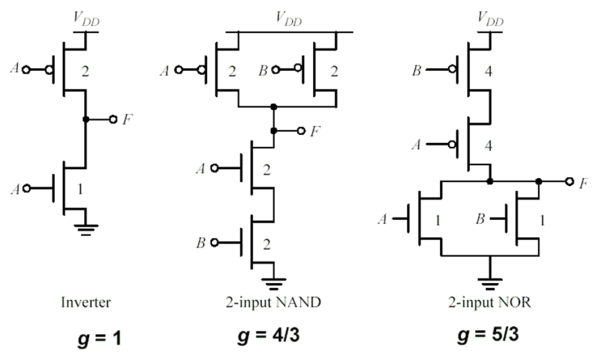
[[File:Fig1-logicaleffort.png|center|thumb|600px|Fig. 1. Logical Effort of Static CMOS Gates]] | [[File:Fig1-logicaleffort.png|center|thumb|600px|Fig. 1. Logical Effort of Static CMOS Gates]] | ||
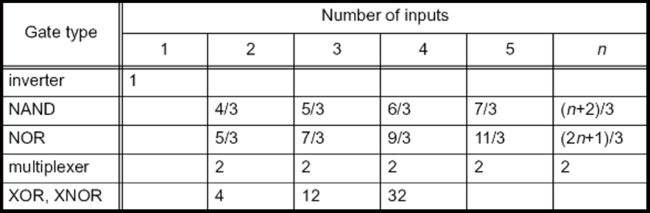
| − | [[File:Tab1-logicaleffort.png|center|thumb| | + | [[File:Tab1-logicaleffort.png|center|thumb|650px|Table 1. Logical Effort of Static CMOS Gates]] |
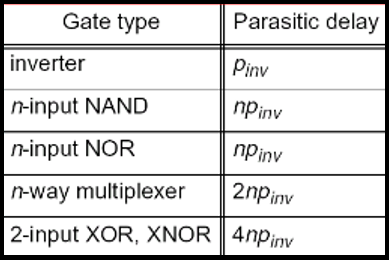
[[File:Tab2-parasitic.png|center|thumb|400px|Table 2. Parasitic Delay of Static CMOS Gates]] | [[File:Tab2-parasitic.png|center|thumb|400px|Table 2. Parasitic Delay of Static CMOS Gates]] | ||
Revision as of 07:59, 10 March 2021
In this lecture, we will cover the following:
- Delay Parameters
- Logical Effort of Simple Gates
- Multistage Networks
Use the provided slide deck to guide you through this discussion. The main reference for this lecture is Sutherland's book[1] and paper[2].
Delay
The delay of a path is equal to the sum of individual gate delays and the delay through the interconnect lines. Each gate delay can be decomposed into its intrinsic delay, p, and the effort delay, f. The effort delay is given by f = gh, where g is the logical effort and h is the effective fanout = Cout / Cin.
Logical Effort
Logical effort is a function of the gate topology and is independent of sizing. It represents the ratio of its input capacitance to the inverter capacitance when size to deliver the same current. The logical effort of the INV, NAND2 and NOR2 are shown in Fig. 1. The simplest gate is the inverter, with an input capacitance of 3Cmin (2Cmin from pmos and Cmin from nmos). For the NAND2, each input sees 2Cmin from pmos and 2Cmin from nmos, giving a logical effort g = 4/3. The logical effort of other static CMOS gates is shown in Table 1. The parasitic delays of static CMOS gates are shown in Table 2.
Multistage Networks
The delay