|
|
| Line 2: |
Line 2: |
| | | | |
| | == Example: A passive band-pass filter == | | == Example: A passive band-pass filter == |
| | + | [[File:LC band-pass.png|thumb|300px|Figure 1: A passive LC band-pass filter.]] |
| | Consider the LC band-pass filter shown in Fig. 1. We can write the transfer function as: | | Consider the LC band-pass filter shown in Fig. 1. We can write the transfer function as: |
| | | | |
| Line 33: |
Line 34: |
| | </math>|{{EquationRef|5}}}} | | </math>|{{EquationRef|5}}}} |
| | | | |
| | + | [[File:Lossy inductor.png|thumb|400px|Figure 2: A lossy inductor.]] |
| | Let us now consider a lossy inductor with <math>Q_\text{ind}= 40=\tfrac{\omega_0 L}{R_s}</math>. The loss can then be modeled by the series resistance, <math>R_s</math>, as shown in Fig. 2, with: | | Let us now consider a lossy inductor with <math>Q_\text{ind}= 40=\tfrac{\omega_0 L}{R_s}</math>. The loss can then be modeled by the series resistance, <math>R_s</math>, as shown in Fig. 2, with: |
| | | | |
| Line 39: |
Line 41: |
| | </math>|{{EquationRef|6}}}} | | </math>|{{EquationRef|6}}}} |
| | | | |
| − | We can convert the series RL circuit to its parallel circuit equivalent in Fig. 3 for frequencies around <math>\omega_0</math> by first writing out the admittance of the series RL circuit as: | + | We can convert the series RL circuit to its parallel circuit equivalent in Fig. 2 at <math>\omega = \omega_0</math> by first writing out the admittance of the series RL circuit as: |
| | | | |
| | {{NumBlk|::|<math> | | {{NumBlk|::|<math> |
Revision as of 10:55, 30 March 2021
Passive RLC filters are simple and easy to design and use. However, can we implement them on-chip? Let us look at a simple example to give us a bit more insight regarding this question.
Example: A passive band-pass filter
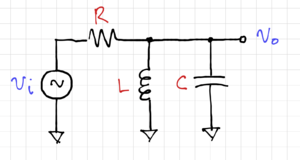
Figure 1: A passive LC band-pass filter.
Consider the LC band-pass filter shown in Fig. 1. We can write the transfer function as:
-
 |
|
(1)
|
If we let  and
and  , then we can rewrite our expression for
, then we can rewrite our expression for  as:
as:
-
 |
|
(2)
|
Notice that the transfer function has two zeros,  , and two poles located at:
, and two poles located at:
-
 |
|
(3)
|
We get complex conjugate poles if  or when
or when  , or equivalently, when
, or equivalently, when  . If the band-pass filter has
. If the band-pass filter has  ,
,  , and
, and  :
:
-
 |
|
(4)
|
-
 |
|
(5)
|

Figure 2: A lossy inductor.
Let us now consider a lossy inductor with  . The loss can then be modeled by the series resistance,
. The loss can then be modeled by the series resistance,  , as shown in Fig. 2, with:
, as shown in Fig. 2, with:
-
 |
|
(6)
|
We can convert the series RL circuit to its parallel circuit equivalent in Fig. 2 at  by first writing out the admittance of the series RL circuit as:
by first writing out the admittance of the series RL circuit as:
-
 |
|
(7)
|
Thus, we get:
-
 |
|
(8)
|
-
 |
|
(9)
|
For  , we get almost no change in the inductor value, or equivalently
, we get almost no change in the inductor value, or equivalently  . We can then redraw our band-pass filter with the lossy inductor model, as shown in Fig. 4. Thus, the new transfer function is then:
. We can then redraw our band-pass filter with the lossy inductor model, as shown in Fig. 4. Thus, the new transfer function is then:
-
 |
|
(10)
|
Note that  remains approximately the same, and the overall quality factor,
remains approximately the same, and the overall quality factor,  , becomes:
, becomes:
-
 |
|
(11)
|
We can then plot the magnitude response of both the ideal LC band-pass filter and the filter with a lossy inductor, as shown in Fig. 5. Note the significant degradation of the magnitude response peak, and the increase in bandwidth when we used an inductor with finite quality factor.
For the ideal case, with a lossless inductor:
-
 |
|
(12)
|
For the filter with a lossy inductor, with  , and from the magnitude response in Fig. 5, we can get:
, and from the magnitude response in Fig. 5, we can get:
-
 |
|
(13)
|
Note that our approximation gives a reasonable estimate of the filter quality factor:
-
 |
|
(14)
|
































