Passive RLC filters are simple and easy to design and use. However, can we implement them on-chip? Let us look at a simple example to give us a bit more insight regarding this question.
Example: A passive band-pass filter
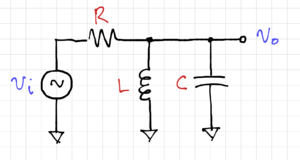
Figure 1: A passive LC band-pass filter.
Consider the LC band-pass filter shown in Fig. 1. We can write the transfer function as:
-
 |
|
(1)
|
If we let  and
and  , then we can rewrite our expression for
, then we can rewrite our expression for  as:
as:
-
 |
|
(2)
|
Notice that the transfer function has two zeros,  , and two poles located at:
, and two poles located at:
-
 |
|
(3)
|
We get complex conjugate poles if  or when
or when  , or equivalently, when
, or equivalently, when  . If the band-pass filter has
. If the band-pass filter has  ,
,  , and
, and  :
:
-
 |
|
(4)
|
-
 |
|
(5)
|
A Lossy Inductor

Figure 2: A lossy inductor.
Let us now consider a lossy inductor with  . The loss can then be modeled by the series resistance,
. The loss can then be modeled by the series resistance,  , as shown in Fig. 2, with:
, as shown in Fig. 2, with:
-
 |
|
(6)
|
We can convert the series RL circuit to its parallel circuit equivalent in Fig. 2 at  by first writing out the admittance of the series RL circuit as:
by first writing out the admittance of the series RL circuit as:
-
 |
|
(7)
|
Note that though this transformation is valid only at  , we will use it to approximate the behavior at frequencies close to
, we will use it to approximate the behavior at frequencies close to  . Thus, we get:
. Thus, we get:
-
 |
|
(8)
|
-
 |
|
(9)
|

Figure 3: A lossy LC band-pass filter.
For  , we get almost no change in the inductor value, or equivalently
, we get almost no change in the inductor value, or equivalently  . We can then redraw our band-pass filter with the lossy inductor model, as shown in Fig. 3. Thus, the new transfer function is then:
. We can then redraw our band-pass filter with the lossy inductor model, as shown in Fig. 3. Thus, the new transfer function is then:
-
 |
|
(10)
|
Note that  remains approximately the same, and the overall quality factor,
remains approximately the same, and the overall quality factor,  , becomes:
, becomes:
-
 |
|
(11)
|
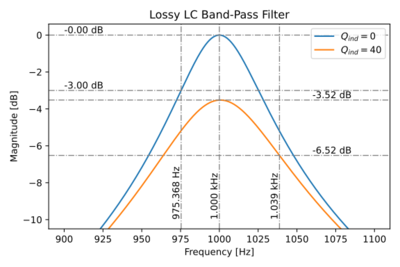
Figure 4: The magnitude response of a band-pass LC filter.
We can then plot the magnitude response of both the ideal LC band-pass filter and the filter with a lossy inductor, as shown in Fig. 4. Note the significant degradation of the magnitude response peak, and the increase in bandwidth when we used an inductor with finite quality factor.
For the ideal case, with a lossless inductor:
-
 |
|
(12)
|
For the filter with a lossy inductor, with  , and from the magnitude response in Fig. 4, we can get:
, and from the magnitude response in Fig. 4, we can get:
-
 |
|
(13)
|
Note that our approximation gives a reasonable estimate of the filter quality factor:
-
 |
|
(14)
|
On-Chip Inductors
In most cases, the inductor implementation limits the use of on-chip passive filters. Consider the on-chip planar inductors, or inductors lying on a single plane, shown in Figs. 5 and 6.
 Figure 5: On-chip spiral inductor layout [1]. |
 Figure 6: On-chip spiral inductor chip photograph [1]. |
Due to the limited metal layers that can be used, the inductor is implemented as spiral inductors, where the diameter of the turns are not constant. Thus, this implementation consumes a large amount of area, and hence large parasitic capacitances. Note that the larger the inductor, the larger the parasitic capacitance. This reduces the self-resonant frequency of the inductor, limiting its frequency of operation, as shown on the top of Fig. 7 The small conductor cross section of the inductor also increases its resistive losss, leading to lower quality factors, as seen in Fig. 7.
 Figure 7: On-chip inductor quality factors [2]. |
It can be seen from Fig. 7 that for reasonable inductance values, e.g.  , we get
, we get  , and can be used for applications where
, and can be used for applications where  . However, typical analog/digital interface circuits typically require lower
. However, typical analog/digital interface circuits typically require lower  frequencies.
frequencies.
Given this, can we build filters without inductors? Yes, by using active elements such as integrators, we can build active filters. It turns out we can easily convert our passive RLC filters into active integrator-based filters using signal flow graphs.
References
- ↑ Jump up to: 1.0 1.1 T. Abaya; D.M. Ancajas; A. Ballesil-Alvarez; L. Alarcon, 0.6V Correlators for WLAN Receivers, Proceedings of the IEEE Sarnoff Symposium, New Jersey, USA. March 30 – April 1, 2009. (ISBN: 978-1-4244-2483-2)
- ↑ L. E. Larson, Silicon technology tradeoffs for radio-frequency/mixed-signal systems-on-a-chip, IEEE Transactions on Electron Devices, vol. 50, no. 3, pp. 683-699, March 2003, doi: 10.1109/TED.2003.810482.









































