Difference between revisions of "Butterworth Filters"
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
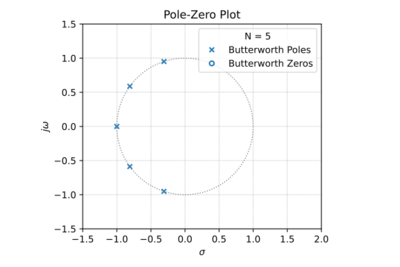
| − | [[File:Butterworth mag.svg|thumb|400px|Figure | + | [[File:Butterworth pz plot.svg|thumb|400px|Figure 1: The Butterworth low-pass pole-zero plot for <math>N=5</math>.]] |
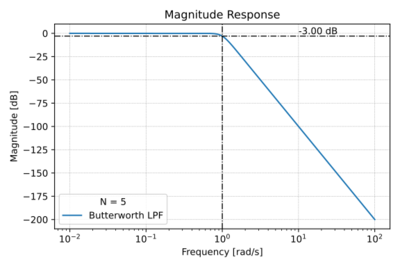
| + | [[File:Butterworth mag.svg|thumb|400px|Figure 2: The Butterworth low-pass filter magnitude response for <math>N=5</math>.]] | ||
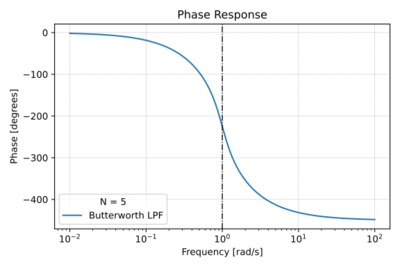
| + | [[File:Butterworth phase.svg|thumb|400px|Figure 3: The Butterworth low-pass filter phase response for <math>N=5</math>.]] | ||
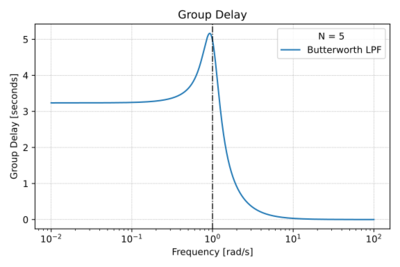
| + | [[File:Butterworth group delay.svg|thumb|400px|Figure 4: The Butterworth low-pass filter group delay for <math>N=5</math>.]] | ||
| − | Butterworth filters are a class of ''all-pole filters'', where the poles of the normalized transfer function are equally spaced along the unit circle (<math>\omega_0 = 1\,\ | + | Butterworth filters are a class of ''all-pole filters'', where the poles of the normalized transfer function are equally spaced along the unit circle (<math>\omega_0 = 1\,\mathrm{\tfrac{rad}{s}}</math>), seen in Fig. 1 for <math>N=5</math>. This results in a '''maximally flat''' pass-band magnitude response as shown in Fig. 2, or equivalently: |
{{NumBlk|::|<math> | {{NumBlk|::|<math> | ||
| Line 7: | Line 10: | ||
</math>|{{EquationRef|1}}}} | </math>|{{EquationRef|1}}}} | ||
| − | This means that the <math>N^\text{th}</math> derivative of the magnitude at DC is zero. | + | This means that the <math>N^\text{th}</math> derivative of the magnitude at DC is zero. Note the <math>-100\,\text{dB}</math> roll-off for <math>N=5</math>, as expected. |
== The Low-Pass Butterworth Filter == | == The Low-Pass Butterworth Filter == | ||
| Line 62: | Line 65: | ||
H\left(s\right) = \frac{1}{\displaystyle \prod_{k=1}^N \frac{s-p_k}{\omega_0}} | H\left(s\right) = \frac{1}{\displaystyle \prod_{k=1}^N \frac{s-p_k}{\omega_0}} | ||
</math>|{{EquationRef|9}}}} | </math>|{{EquationRef|9}}}} | ||
| + | |||
| + | We can also plot the phase response as illustrated in Fig. 3, and taking the derivative of the phase, we get the group delay plot in Fig. 4. Note that there is moderate phase distortion around <math>\omega_0</math>. | ||
Latest revision as of 00:17, 16 March 2021
Butterworth filters are a class of all-pole filters, where the poles of the normalized transfer function are equally spaced along the unit circle (), seen in Fig. 1 for . This results in a maximally flat pass-band magnitude response as shown in Fig. 2, or equivalently:
-
(1)
-
This means that the derivative of the magnitude at DC is zero. Note the roll-off for , as expected.
The Low-Pass Butterworth Filter
The low-pass Butterworth filter has the following magnitude response:
-
(2)
-
Where is the filter order and is the frequency. Note that at . Thus:
-
(3)
-
Thus, the poles are the roots of:
-
(4)
-
Or equivalently:
-
(5)
-
Since we can write , the roots of can be written as:
-
(6)
-
For . Thus, we get:
-
(7)
-
Solving for , we get the poles of the low-pass Butterworth filter:
-
(8)
-
We can then write:
-
(9)
-
We can also plot the phase response as illustrated in Fig. 3, and taking the derivative of the phase, we get the group delay plot in Fig. 4. Note that there is moderate phase distortion around .