Difference between revisions of "229-A2.1"
| Line 31: | Line 31: | ||
* We choose the number of samples to be integer powers of 2, e.g. 1024, 2048, 4096, etc. so we can take advantage of the FFT algorithm's speedup. | * We choose the number of samples to be integer powers of 2, e.g. 1024, 2048, 4096, etc. so we can take advantage of the FFT algorithm's speedup. | ||
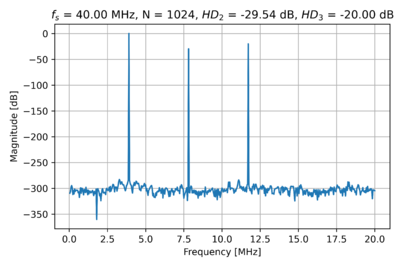
| − | For example, let us set a sampling frequency, <math>f_s = 40\,\mathrm{MHz}</math>, and generate a sinusoid with 673 periods, with the number of samples <math>N=2^10=1024</math>. Let us then choose a sinusoid that is an integer multiple of <math>\ | + | For example, let us set a sampling frequency, <math>f_s = 40\,\mathrm{MHz}</math>, and generate a sinusoid with 673 periods, with the number of samples <math>N=2^{10}=1024</math>. Let us then choose a sinusoid that is an integer multiple of <math>\tfrac{f_s}{N}</math>. Thus, we get <math>f_\mathrm{in}=100\cdot \tfrac{f_s}{N}=3.90625\,\mathrm{MHz}</math>. The spectrum of our single sinusoid is shown in Fig. 3. |
{| | {| | ||
Revision as of 11:53, 21 September 2020
Activity: Nonlinearity in Circuits
- Instructions: This activity is structured as a tutorial with a design problem at the end. Should you have any questions, clarifications, or issues, please contact your instructor as soon as possible.
- At the end of this activity, the student should be able to:
- Understand and observe the effects of nonlinearity in electronic circuits.
Visualizing Nonlinearity
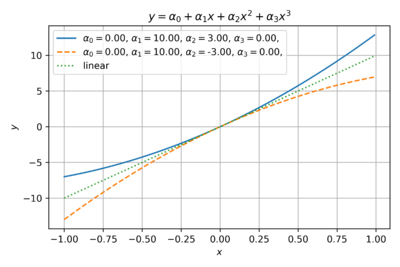
Let us examine the effects of varying the coefficients of the power series model of our transfer function. Fig. 1 shows the an even function with only second order coefficients. This is typical of ideal square-law single-ended MOS amplifiers where a quadratic term dominates.
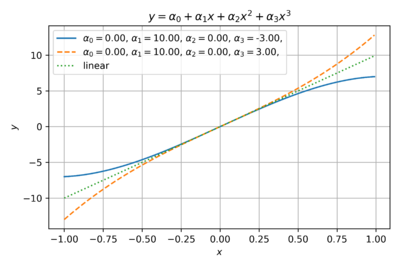
Fig. 2 shows an odd function with only third order coefficients. This is a good estimate for differential circuits, where the common-mode terms cancel out. For example, the outputs of a differential amplifier can be expressed as:
-
(1)
-
-
(2)
-
Then the differential output is:
-
(3)
-
We can also see from Fig. 2 that the negative third (and other odd) order coefficients model the output saturation in real amplifiers as the output level approaches the supply voltages. Thus, in most cases, the third order nonlinearity dominates.
Spectral Response
Let us also try to visualize the effects of nonlinearity in the frequency domain, where our main tool would be the discrete Fourier transform (DFT) or the fast Fourier transform (FFT). When performing an FFT, we want our sinusoids (or tones) to fall into just one frequency bin. To do this, we must make sure that:
- We use a sampling frequency much higher than twice our highest frequency of interest, or .
- We choose a prime number of whole periods so we do not get spurious tones in the frequency response. Note that the FFT assumes the input is periodic. If not, we will get spectral leakage.
- We choose the number of samples to be integer powers of 2, e.g. 1024, 2048, 4096, etc. so we can take advantage of the FFT algorithm's speedup.
For example, let us set a sampling frequency, , and generate a sinusoid with 673 periods, with the number of samples . Let us then choose a sinusoid that is an integer multiple of . Thus, we get . The spectrum of our single sinusoid is shown in Fig. 3.
If we pass this input sinusoid through a nonlinear stage with , , and , we get the spectrum in Fig. 4. As expected, we get the second and third harmonic frequency components at and respectively.