229-A2.1

Activity: Nonlinearity in Circuits

• Instructions: This activity is structured as a tutorial with a design problem at the end. Should you have any questions, clarifications, or issues, please contact your instructor as soon as possible.
• At the end of this activity, the student should be able to:

1. Understand and observe the effects of nonlinearity in electronic circuits.

Visualizing Nonlinearity

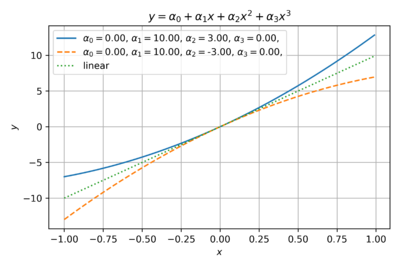
Let us examine the effects of varying the coefficients of the power series model of our transfer function. Fig. 1 shows the an even function with only second order coefficients. This is typical of ideal square-law single-ended MOS amplifiers where a quadratic term dominates.

Figure 1: An even function with positive and negative second order coefficients.

Figure 2: An odd function with positive and negative third order coefficients.

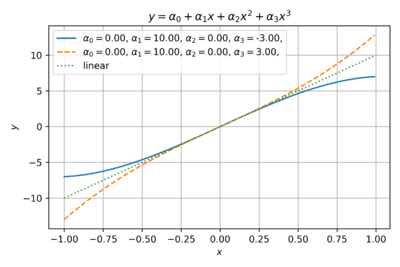
Fig. 2 shows an odd function with only third order coefficients. This is a good estimate for differential circuits, where the common-mode terms cancel out. For example, the outputs of a differential amplifier can be expressed as:

$v_{\mathrm {o} }^{+}=\alpha _{0}+\alpha _{1}\left({\frac {v_{\mathrm {id} }}{2}}\right)+\alpha _{2}\left({\frac {v_{\mathrm {id} }}{2}}\right)^{2}+\alpha _{3}\left({\frac {v_{\mathrm {id} }}{2}}\right)^{3}$

(1)

$v_{\mathrm {o} }^{-}=\alpha _{0}+\alpha _{1}\left(-{\frac {v_{\mathrm {id} }}{2}}\right)+\alpha _{2}\left(-{\frac {v_{\mathrm {id} }}{2}}\right)^{2}+\alpha _{3}\left(-{\frac {v_{\mathrm {id} }}{2}}\right)^{3}$

(2)

Then the differential output $v_{\mathrm {o} }^{+}-v_{\mathrm {o} }^{-}=v_{\mathrm {od} }$ is:

$v_{\mathrm {od} }=\alpha _{1}v_{\mathrm {id} }+{\frac {\alpha _{3}}{4}}v_{\mathrm {id} }^{3}$

(3)