CoE 197U Two-Stage MOS Operational Transconductance Amplifiers

If a larger gain than that of a differential amplifier is needed, the next step is to use cascade amplifier stage/s or cascode the differential pair. Cascoding uses common-gate amplifiers/buffers to increase gain at the cost of reduced voltage swing. Meanwhile, cascading can achieve larger voltage swings but need separate current paths and therefore, consume more power. With nominal supply voltages decreasing with technology, cascoding becomes less viable. In this lecture, we will look at a typical 2-stage MOS amplifier.

The main reference for this topic is chapter 6.3 of the Analysis and Design of Analog Integrated Circuits book.

Op-amps and OTA

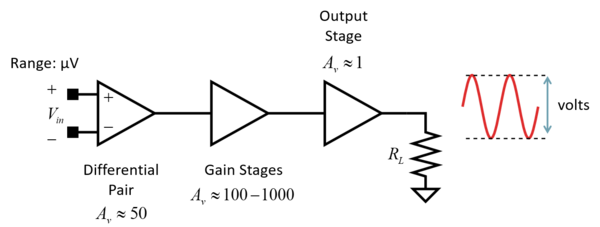
An operational amplifier or op-amp can be roughly divided into three stages (Fig. 1): the differential pair, the gain stage/s, and the output stage. The differential pair enables the op-amp to have a differential input, have a large input resistance, and provide some gain. The gain stage/s provide the additional gain needed, but in doing so, end up with a large output resistance that cannot drive heavy (low resistance) resistive loads. The output stage provides a gain of 1 or less. It is added to give the op-amp low output resistance, large output swing, and the ability to provide large output currents.

Figure 1: Generalized op-amp blocks

Figure 2: Op-amp symbol visualized as a combination of an OTA symbol and a buffer

The differential and gain stages combined can be viewed as an OTA or operational transconductance amplifier. Thus, the op-amp can be viewed as an OTA with an output buffer (Fig. 2). OTAs have large gain and large output resistance. An OTA produces an output current from an input voltage and can drive capacitive loads (provide charging current) which are common in on-chip loads (e.g. gate of another MOSFET). A low output resistance is not necessarily required in driving capacitive loads.

Miller OTA

The Miller OTA is a simple 2-stage OTA composed of a current mirror-loaded differential pair stage and a common source stage (Fig. 3). It is one of the go-to amplifiers in IC design because of its simplicity. The topology contains only a few transistors, making it relatively easy to design. The circuit also has a simple biasing scheme. The design of the current source itself is a different story! However, in less critical applications, a resistor can be used in place of the current source. There are many problems associated with the latter scheme. On-chip resistors are not accurate, may occupy large chip area, can change resistance with temperature, and provides current that is sensitive to temperature and supply voltage changes.

Figure 3: Miller OTA Schematic (NMOS input)

This two-stage OTA can be compensated by using a Miller compensating capacitor, $C_{C}$. Compensation is needed to ensure that the amplifier is stable when used in feedback. You may refer to these materials to review the fundamental concepts of feedback and compensation although the Miller compensation is covered only on Lec 12B. If the load capacitance is not large enough to create a dominant pole, then the capacitor $C_{C}$ can be added. Placing a very large capacitor to produce a dominant pole is expensive in terms of chip area. By placing the capacitor $C_{C}$ as shown, a smaller capacitance value (and thus area) is needed since the Miller effect amplifies the capacitance by a factor $g_{m6}\left(r_{o6}\parallel r_{o7}\right)$. This amplified capacitance effectively appears at the input of the common source stage (or output of the differential pair) to ground. With a large enough $C_{C}$, the pole associated with the output of the differential pair can be made dominant to ensure stability.

Before proceeding, note that the analysis to be presented assumes that all transistors are saturated square law devices described by the equations below (for NMOS). The term overdrive voltage or $V_{OV}$ is used to refer to $V_{GS}-V_{TH}$ or $V_{DSAT}$. For PMOS devices, $V_{OV}$ refers to $\left|V_{GS}\right|-\left|V_{TH}\right|$. The paired devices (M1 and M2, and M3 and M4) have the same dimensions. All NMOS transistors are also assumed to have the same threshold voltage $V_{THn}$ while all PMOS transistors are assumed to have the same threshold voltage $V_{THp}$.

$I_{D}={\frac {k'}{2}}{\frac {W}{L}}\left(V_{GS}-V_{TH}\right)^{2}\left(1+\lambda V_{DS}\right)={\frac {k'}{2}}{\frac {W}{L}}\left(V_{OV}\right)^{2}\left(1+\lambda V_{DS}\right)$

$g_{m}={\frac {2I_{D}}{V_{OV}}}={\sqrt {2k'{\frac {W}{L}}I_{D}}}$

$r_{o}={\frac {1}{\lambda I_{D}}}$

AC Analysis (Low Frequency)

The AC characteristics will be discussed first to evaluate the impact of design decisions done when sizing and biasing the transistors at DC. Only very low frequencies are considered such that the capacitor $C_{C}$ is still open and can be disregarded.

Gain

The input resistance of the 2nd stage, the common source stage, is infinite. Thus, there will be no loading between the two stages. The overall low-frequency small-signal gain of the Miller OTA is simply $A_{v}=A_{v,dp}\cdot A_{v,cs}$. From the differential pair discussion , it was shown that the gain of an NMOS-input differential pair is some $g_{mn}\left(r_{on}\parallel r_{op}\right)$. Meanwhile, the gain of a PMOS common source amplifier with an NMOS active load is some $g_{mp}\left(r_{op}\parallel r_{on}\right)$.

$A_{v,dp}=g_{m1}\left(r_{o2}\parallel r_{o4}\right)$

$A_{v,cs}=-g_{m6}\left(r_{o6}\parallel r_{o7}\right)$

$A_{v}=-g_{m1}\left(r_{o2}\parallel r_{o4}\right)\cdot g_{m6}\left(r_{o6}\parallel r_{o7}\right)$

(1)

The differential pair stage’s gain is non-inverting since the negative terminal of the input is at the output side. On the other hand, the common source stage is inverting. The overall gain of the two-stage OTA is inverting. If a non-inverting gain is desired, the input connection can just be switched (positive terminal of the input at M2 gate instead). It can also be said that the gain is related to some $\left(g_{m}r_{o}\right)^{2}$ quantity.

Output Resistance

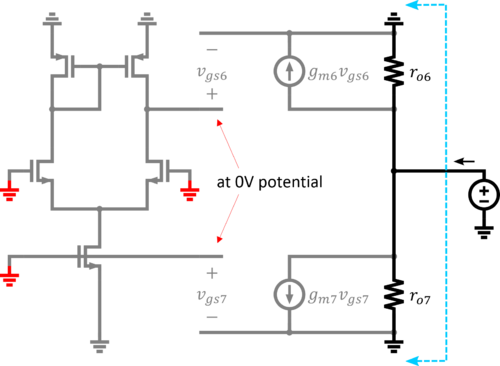
The output resistance can be determined by grounding the input and placing a test source at the output. Since the input to the differential pair is zero, its output must also be zero. Since the source of M6 is also grounded, then $v_{gs6}=0$. At the bottom, the gate of M7 is connected to some DC bias which is an AC ground. Since the source of M7 is also grounded, then $v_{gs7}=0$. With the help of Fig. 4, it is easy to see that the output impedance is just $r_{o6}$ and $r_{o7}$ in parallel.

$R_{o}=r_{o6}\parallel r_{o7}$

(2)

Figure 4: Simplified small-signal circuit in determining Ro for the Miller OTA

Transconductance

From the overall gain (Eq. 1) and output resistance (Eq. 2), it can be inferred from $A_{v}=-G_{m}R_{o}$ that

$G_{m}=g_{m1}\left(r_{o2}\parallel r_{o4}\right)\cdot g_{m6}$

(3)

Input Resistance

The input resistance of the OTA is the input resistance of the differential pair which is also infinite.

$R_{i}\rightarrow \infty$

(4)

Discussion

The output impedance can be expressed in terms of $\lambda$ and $I_{D}$. M6 and M7 share the same branch current (i.e. $I_{D6}=I_{D7}=I_{D,cs}$). However, the $\lambda$ for M6 and M7 are not necessarily the same.

$R_{o}={\frac {{\frac {1}{\lambda _{6}I_{D6}}}\cdot {\frac {1}{\lambda _{7}I_{D7}}}}{{\frac {1}{\lambda _{6}I_{D6}}}+{\frac {1}{\lambda _{7}I_{D7}}}}}={\frac {1}{\left(\lambda _{6}+\lambda _{7}\right)I_{D,cs}}}$

The gain expression can be expanded in the same fashion and using $g_{m}={\frac {2I_{D}}{V_{OV}}}$. Note also that $I_{D1}=I_{D2}=I_{D3}=I_{D4}$.

$A_{v}={\frac {2I_{D1}}{V_{OV1}}}\cdot {\frac {1}{\left(\lambda _{2}+\lambda _{4}\right)I_{D}2}}\cdot {\frac {2I_{D6}}{V_{OV6}}}\cdot {\frac {1}{\left(\lambda _{6}+\lambda _{7}\right)I_{D6}}}$

$A_{v}={\frac {4}{V_{OV1}V_{OV6}\left(\lambda _{2}+\lambda _{4}\right)\left(\lambda _{6}+\lambda _{7}\right)}}$

(5)

The $\lambda$ terms are dictated by the technology or process. $\lambda$ can be decreased to improve gain by increasing the transistor lengths (i.e. less channel length modulation). On the other hand, $V_{OV}$ is a design choice on how to bias the transistors at DC. Decreasing $V_{OV}$ increases the gain. However, decreasing $V_{OV}$ operates the transistor closer to moderate or weak inversion where the transistor $f_{T}$ (transit frequency) is lower. The same is true when increasing the channel length. Thus, while increasing the length and/or decreasing $V_{OV}$ improves the gain, the frequency response of the transistor and of the amplifier is degraded. Note that increasing the current by increasing the transistor widths (but maintaining $V_{OV}$) will not increase the gain but will increase the bandwidth (as long as the parasitic capacitances are much smaller than the load capacitance) at the cost of area and power. These observations are generally true with amplifiers whose gain is based on $g_{m}r_{o}$ or the transistor’s intrinsic gain.

DC Analysis

Since there is no current through the gate of M6, then the two stages can be discussed separately. The differential pair has been analyzed in detail here . If the transistors are perfectly matched, then $I_{D3}=I_{D4}={\frac {I_{D5}}{2}}$ and $\left|V_{GS3}\right|=\left|V_{DS3}\right|=\left|V_{GS4}\right|=\left|V_{DS4}\right|$. This means that the drain nodes of M1-4 must be at the same potential. The output of the differential pair or the drain of M4 must be at . This voltage is the gate voltage seen by M6. Thus, M3, M4, and M5 must have the same gate-to-source voltages.

$V_{D1}=V_{D2}=V_{G6}$

$\left|V_{GS3}\right|=\left|V_{GS4}\right|=\left|V_{GS6}\right|$

With the earlier mentioned assumption that the $V_{TH}$ of all PMOS devices are the same, then the $V_{OV}$ of transistors M3, M4, and M6 must be the same. In process technologies or sizes where the threshold voltage is dependent on the device length, the assumption will only be true if $L_{3}=L_{4}=L_{5}$. Aside from that, using equal device lengths will make layout easier and help match these transistors.

$\left|V_{GS3}\right|-\left|V_{THp}\right|=\left|V_{GS4}\right|-\left|V_{THp}\right|=\left|V_{GS6}\right|-\left|V_{THp}\right|$

$V_{OV3}=V_{OV4}=V_{OV6}$

To make sure that the transistors on the 2nd stage are saturated, the M6 and M7 must be sized and biased for the same drain current (i.e. $I_{D6}=I_{D7}$). While the $V_{OV}$ of M6 is dictated by the $V_{OV}$ of M3 and M4, the $V_{OV}$ of M7 and M5 is dictated by the $V_{OV}$ of M8. Again, this assumes that $V_{TH}$ for M5, M7, and M8 are the same, and using $L_{5}=L_{7}=L_{8}$ helps achieve this.

$V_{GS5}=V_{GS7}=V_{GS8}$

$V_{GS5}-V_{THn}=V_{GS7}-V_{THn}=V_{GS8}-V_{THn}$

$V_{OV5}=V_{OV7}=V_{OV8}$

Fig. 3 shows that the dimensions of M5 and M7 are related by a proportion of $1:N$ (i.e. M7’s width-to-length ratio is N times larger than that of M5). Since the transistors have the same $V_{GS}$, then the constant $N$ can be also used to refer to the ratio of drain currents assuming the effect of CLM is negligible.

${\frac {1}{N}}={\frac {\left({\frac {W_{5}}{L_{5}}}\right)}{\left({\frac {W_{7}}{L_{7}}}\right)}}$

$N={\frac {\left({\frac {W_{7}}{L_{7}}}\right)}{\left({\frac {W_{5}}{L_{5}}}\right)}}={\frac {I_{D7}}{I_{D5}}}$

At DC, half of the tail current flows through M3 and M4 (i.e. $I_{D3}=I_{D4}={\frac {I_{D5}}{2}}$). Thus, the sizes of M4 and M5 must be related by a proportion of $1:2N$.

$I_{D4}={\frac {I_{D5}}{2}}$

$I_{D6}=I_{D7}$

${\frac {I_{4}}{I_{6}}}={\frac {1}{2N}}={\frac {\left({\frac {W_{4}}{L_{4}}}\right)}{\left({\frac {W_{6}}{L_{6}}}\right)}}$

Thus, for example, if $N=0.5$ or $I_{7}={\frac {1}{2}}I_{5}$, then M6 must be as large as M4.

Effects of Mismatch

Assume that all transistors that must be matched are perfectly matched, except possibly M1 and M2. Let $I_{D1}=\alpha I_{D2}$ where $\alpha =1$ only when M1 and M2 are perfectly matched. By KCL, this means that $I_{D3}=\alpha I_{D4}$ as well, even though M3 and M4 are perfectly matched. Note that $V_{GS3}=V_{GS4}$ still, since their gates and sources are shorted. Thus, since M3 and M4 are matched ($V_{TH3}=V_{TH4}$, $k'_{p3}=k'_{p4}$, $W_{3}=W_{4}$, etc.), the only way for their currents to be different is by having different drain-source voltages. Let $\lambda _{3}=\lambda _{4}=\lambda _{p}$.

$I_{D3}=\alpha I_{D4}$

${\frac {k'_{3}}{2}}{\frac {W_{3}}{L_{3}}}\left(\left|V_{GS3}\right|-\left|V_{THp}\right|\right)^{2}\left(1+\lambda _{3}V_{SD3}\right)=\alpha {\frac {k'_{4}}{2}}{\frac {W_{4}}{L_{4}}}\left(\left|V_{GS4}\right|-\left|V_{THp}\right|\right)^{2}\left(1+\lambda _{4}V_{SD4}\right)$

$1+\lambda _{3}V_{SD3}=\alpha \left(1+\lambda _{4}V_{SD4}\right)$

$V_{SD4}={\frac {{\frac {1}{\lambda _{p}}}+V_{SD3}}{\alpha }}-{\frac {1}{\lambda _{p}}}$

(6)

Suppose the circuit is designed for 1V supply, $\left|V_{GS3}\right|=\left|V_{DS3}\right|=0.4V$. The output of the differential pair stage will ideally be at 0.6V. Suppose that $\lambda _{p}=0.01V^{-1}$ and that M1 and M2 were mismatched such that $\alpha =0.99$. By KCL, $I_{T}=I_{D1}+I_{D2}=\left(1+\alpha \right)I_{D1}$ which means that $I_{D1}$ will be slightly off from ${\frac {I_{T}}{2}}$. However, assume that the change is small enough such that $V_{SG3}=V_{SD4}$ stays approximately at 0.4V. By Eq. 6, it can be shown that $V_{SD4}$ will tend to be at 1.414V. This of course cannot happen since the supply is only 1V. However, this suggests that the output will rail, and the transistors will not anymore be saturated even if $\alpha =0.99$, which is just off by 0.01 from the ideal case of 1.

Another way of looking at the mismatch problem is by lumping the effects of mismatch and referring them into the input, also called the input-referred offset voltage. The input-referred offset voltage caused by mismatch from the differential pair stage can be shown to follow Eq. 7.

$V_{offset,i}\cong \Delta V_{TH\left(1-2\right)}+\Delta V_{TH\left(3-4\right)}{\frac {g_{m3}}{g_{m1}}}+{\frac {\Delta V_{OV\left(1-2\right)}}{2}}\left[{\frac {\Delta \left({\frac {W}{L}}\right)_{\left(3-4\right)}}{\left({\frac {W}{L}}\right)_{\left(3-4\right)}}}-{\frac {\Delta \left({\frac {W}{L}}\right)_{\left(1-2\right)}}{\left({\frac {W}{L}}\right)_{\left(1-2\right)}}}\right]$

(7)

The first 2 terms are caused by difference ($\Delta$) in threshold voltages of M1 and M2, and M3 and M4, respectively. The effect of the second term can be reduced by making $g_{m3}<g_{m1}$. This can be done by sizing the W/L ratio of M3 and M4 to be smaller than that of M1 and M2 since $g_{m}={\sqrt {2k'{\frac {W}{L}}I_{D}}}$. Alternatively, ${\frac {g_{m3}}{g_{m1}}}={\frac {V_{OV1}}{V_{OV3}}}$ which means that the second term can be reduced by using a larger overdrive voltage for the current mirror-load compared to the differential pair. The third term is caused by mismatches in device dimensions. The effect of this term can be reduced by making the transistors themselves large, such that minor differences in size due to etching imperfections will be relatively small or negligible. The effect can also be reduced by operating the input transistors with a low overdrive voltage.

This input-referred offset adds to the actual input. If there is no input yet, the offset remains and is amplified at the output. That is why in the analysis with $\alpha =0.99$, the output still railed because of the gain of the amplifier. Note also that the change in the output of the differential pair will also be amplified by the common source stage so the offset’s effect at the actual output will be larger.