SFG RLC Filter Example

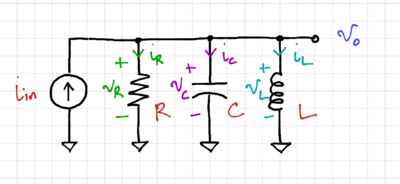
Consider the second-order RLC Filter shown in Fig. 1. Let us use signal flow graphs to convert this passive filter into an equivalent active filter.

Figure 1: A passive RLC band-pass filter.

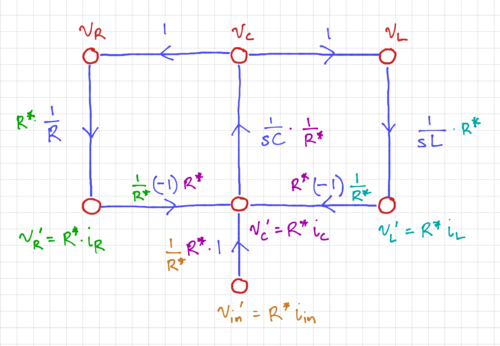
After labeling the node voltages and branch currents, we then express the inductor currents and capacitor voltages as integrator forms, as shown in the signal flow graph in Fig. 2.

Figure 2: The initial signal flow graph of the passive RLC band-pass filter.

We then normalize the signal flow graph to convert the current nodes into voltage nodes, as shown in Figs. 3 and 4.

Figure 3: Normalizing the signal flow graph to convert the current nodes into voltage nodes.

Figure 4: The resulting normalized signal flow graph.

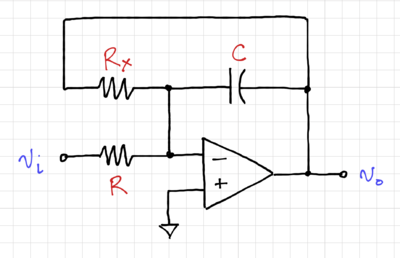
The integrator-based active filter can then be derived, as seen in Fig. 5, with $\tau _{1}=CR^{*}$ and $\tau _{2}={\tfrac {L}{R^{*}}}$.

Figure 5: The integrator-based equivalent active filter.

Using signal flow graphs, we have converted the passive RLC band-pass filter to an equivalent inductor-less active filter, composed only of integrators, a gain stage with a gain of ${\tfrac {R^{*}}{R}}$, and a summing circuit. In practice, we can combine the summation and the gain into the op-amp circuit, as shown in Fig. 6.

Figure 6: Combining the summation, integration, and gain in a single op-amp circuit.

The output is then:

${\begin{aligned}v_{o}&=-{\frac {1}{sCR}}\cdot v_{i}-{\frac {1}{sCR}}\cdot \left(v_{o}\cdot {\frac {R^{*}}{R}}\right)&=-{\frac {1}{sCR}}\cdot v_{i}-{\frac {1}{sC\cdot R{\frac {R}{R^{*}}}}}\cdot v_{o}\\&=-{\frac {1}{sCR}}\cdot v_{i}-{\frac {1}{sCR_{x}}}\cdot v_{o}\\\end{aligned}}$

(1)

Thus, the integrator with time constant $\tau _{1}$ and the gain ${\tfrac {R^{*}}{R}}$ can be combined into a single op-amp circuit with $R_{x}={\tfrac {R^{2}}{R^{*}}}$. We will look at a more detailed circuit implementation later, since we still have a few issues left to tackle, such as how to efficiently perform subtraction together with addition.