Electronic Noise

In this module, we consider the noise generated by the electronic devices themselves due to the (1) random motion of electrons due to thermal energy and (2) the discreteness of electric charge. We see this as thermal noise in resistances, and shot noise in PN junctions. In MOS transistors, we also see flicker noise. This noise is not fundamental, but is due to the way MOS transistors are manufactured, This added uncertainty in the voltages and currents limit the smallest signal amplitude or power that our circuits can detect and/or process, limiting the transmission range and power requirements for reliable communications. Note that purely reactive elements, i.e. ideal inductors and capacitors, do not generate noise, but they can shape the frequency spectrum of the noise.

Modeling Noise

Figure 1: Random movement of an electron in an electric field.

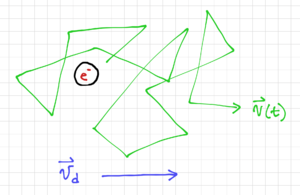
Since electronic noise is random, we cannot predict its value at any given time. However, we can describe noise in terms of its aggregate characteristics or statistics, such as its probability distribution function (pdf). As expected from the Central Limit Theorem, the pdf of the random movement of many electrons would approach a Gaussian distribution with zero mean since the electrons will move around instantaneously, but without any excitation, it will, on the average, stay in the same point in space. If we add an electric field, then the electron will move with an average drift velocity, ${\vec {v}}_{d}=-\mu _{e}{\vec {E}}$, but at any point in time, it would be moving with an instantaneous velocity ${\vec {v}}\left(t\right)\neq {\vec {v}}_{d}$, as shown in Fig. 1. Note that $\mu _{e}$ is the electron mobility.

Noise Power

Aside from the mean, to describe a zero-mean Gaussian random variable, $X$, we need the variance, $\sigma ^{2}=\left\langle X^{2}\right\rangle$, or the mean of $X^{2}$. For random voltages or currents, $n\left(t\right)$, this is equal to the average power over time, normalized to $1\,\mathrm {\Omega }$:

$P_{n}=\lim _{T\rightarrow \infty }{\frac {1}{T}}\int _{0}^{T}n^{2}\left(t\right)dt$

(1)

Figure 2: Zero-mean noise signals in time with different variances.

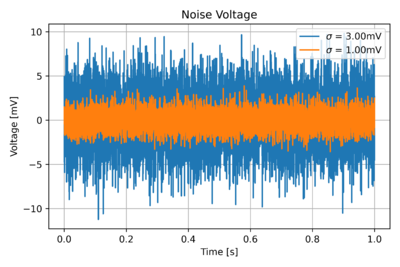
Thus, to describe noise, we can use its variance, or equivalently its average power. Fig. 2 illustrates the difference between two noise signals with different variances. Recall that $\sigma$, the square root of the variance, is the standard deviation.

Consider a noise voltage in time, $v_{n}\!\left(t\right)$, similar to the ones depicted in Fig. 2. The mean is then:

${\overline {v_{n}}}=\lim _{T\rightarrow \infty }{\frac {1}{T}}\int _{0}^{T}v_{n}\!\left(t\right)dt=0$

(2)

The variance, however, is non-zero:

${\overline {v_{n}^{2}}}=\lim _{T\rightarrow \infty }{\frac {1}{T}}\int _{0}^{T}v_{n}^{2}\!\left(t\right)dt\neq 0$

(3)

We can also calculate the root-mean-square or RMS as:

$v_{n,\mathrm {rms} }={\sqrt {\overline {v_{n}^{2}}}}={\sqrt {\lim _{T\rightarrow \infty }{\frac {1}{T}}\int _{0}^{T}v_{n}^{2}\!\left(t\right)dt}}$

(4)

Noise Power Spectrum

Figure 3: The power spectral density of white noise.

We can also examine the noise in the frequency domain, specifically, how noise power is distributed over frequency. Many noise sources are white, i.e. the noise power is distributed evenly across all frequencies, as seen in Fig. 3. Thus, white noise is totally unpredictable in time since there is no correlation between the noise at time $t_{1}$ and the noise at time $t_{1}+\delta$, no matter how small $\delta$ is, since the likelihood of a high frequency change (small $\delta$) and a low frequency change (large $\delta$) are the same.

The noise power should be the same, whether we obtain it from the time or frequency domain. Thus, calculating the noise power in time and in frequency, and equating the two, we get:

$\int _{0}^{\infty }S_{n}\!\left(f\right)df=\lim _{T\rightarrow \infty }{\frac {1}{T}}\int _{0}^{T}v_{n}^{2}\!\left(t\right)dt$

(5)

Where $S_{n}\!\left(f\right)$ is the noise power spectral density in ${\tfrac {V^{2}}{\mathrm {Hz} }}$. An alternate representation of the noise spectrum is the root spectral density, $V_{n}\!\left(f\right)={\sqrt {S_{n}\!\left(f\right)}}$, with units of ${\tfrac {V}{\mathrm {\sqrt {Hz}} }}$.

Signal-to-Noise Ratio

In general, we try to maximize the signal-to-noise ratio (SNR) in a communication system. For an average signal power $P_{\mathrm {signal} }$, and an average noise power $P_{\mathrm {noise} }$, the SNR in dB is defined as:

$\mathrm {SNR} =10\log {\frac {P_{\mathrm {signal} }}{P_{\mathrm {noise} }}}$

(6)

Again note that we are referring to random noise and not interference or distortion.

Resistor Noise

Due to the random thermal motion of charge carriers, we get thermal noise, and we observe it as voltage and current noise in resistive circuit elements that is proportional to absolute temperature. We expect this to be the case since at higher temperatures, electrons and holes have higher energy, leading to larger instantaneous velocities, and thus larger excursions from the mean velocity, e.g. from an electric field-induced drift velocity.

Modeling Thermal Noise in Resistors

Figure 1: Resistor noise generators.

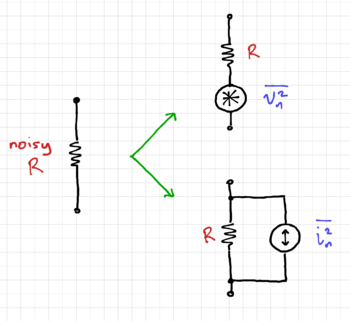
Consider the noisy resistor in Fig. 1. We can model this as a noiseless resistor in series with a voltage noise generator, or a noiseless resistor in parallel with a current noise generator. Since we cannot predict the voltage or current noise at any point in time, we can instead specify the noise mean square voltage spectral density over a unit bandwidth, $\Delta f$:

${\overline {v_{n}^{2}}}=4kTR\Delta f$

(7)

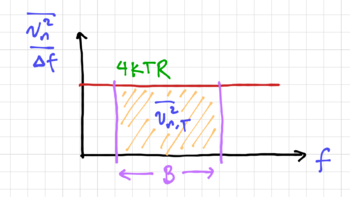
Where $k$ is Boltzmann's constant, equal to $1.38064852\times 10^{-23}\mathrm {\tfrac {J}{K}}$ and $T$ is the temperature in Kelvin. The total integrated noise power is then:

${\overline {v_{n,T}^{2}}}=\int _{B}\left({\frac {\overline {v_{n}^{2}}}{\Delta f}}\right)df=\int _{B}4kTR\,df=4kTRB$

(8)

Where $B$ is the observation bandwidth. Alternatively, we can specify the total integrated noise power from the noise current generator:

${\overline {i_{n,T}^{2}}}=4kTGB={\frac {4kTB}{R}}$

(9)

Figure 2: The resistor noise power spectral density.

Thermal noise is white noise, since ${\tfrac {\overline {v_{n}^{2}}}{\Delta f}}=4kTR$ is constant over frequency, and hence the noise generators have white power spectral densities, as shown in Fig. 2. Just like any small signal, the shape of the power spectral density can be shaped by the frequency response of the rest of the circuit.

Also note that the polarity of the noise generators are intentionally not specified in the symbols shown in Fig. 1, since the noise voltage or current can take on positive or negative values at any given time.

For example, a resistor with $R=10\mathrm {k\Omega }$ at $T=20^{\circ }C=293K$, the voltage noise power is:

${\overline {v_{n,T}^{2}}}=4kTRB=1.62\times 10^{-16}\cdot B$

(10)

Which gives us:

$v_{\mathrm {n,rms} }={\sqrt {\overline {v_{n,T}^{2}}}}={\sqrt {4kTRB}}=1.27\times 10^{-8}\cdot {\sqrt {B}}$

(11)

For a measurement bandwidth of $B=1\mathrm {MHz}$, we get $v_{\mathrm {n,rms} }=13\,\mathrm {\mu V}$. This is the smallest voltage, or the minimum detectable signal we can resolve across this resistor with this bandwidth, i.e. the smallest voltage we can distinguish from the thermal noise of the resistor.

Noise in Resistor Circuits

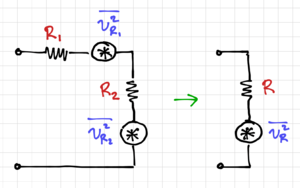
Consider two noisy resistors in series, as shown in Fig. 3. The equivalent resistance of the series circuit is $R=R_{1}+R_{2}$, and since we can sum the voltage noise powers, we get:

${\overline {v_{R}^{2}}}={\overline {v_{R_{1}}^{2}}}+{\overline {v_{R_{2}}^{2}}}=4kTR_{1}\Delta f+4kTR_{1}\Delta f=4kT\left(R_{1}+R_{2}\right)\Delta f=4kTR\Delta f$

(12)

It is important to remember that the noise power is additive, but the noise voltages and currents are not, since we do not know the phase of these signals at a given point in time. Similarly, for the parallel resistor circuit in Fig. 4, the equivalent conductance is $G=G_{1}+G_{2}$, and the resulting equivalent current noise generator is:

${\overline {i_{G}^{2}}}={\overline {i_{G_{1}}^{2}}}+{\overline {i_{G_{2}}^{2}}}=4kTG_{1}\Delta f+4kTG_{1}\Delta f=4kT\left(G_{1}+G_{2}\right)\Delta f=4kTG\Delta f$

(13)

Figure 3: Equivalent noise generators for resistors in series.

Figure 4: Equivalent noise generators for resistors in parallel.

In adding the noise powers, we assumed that the noise generators are independent of each other, i.e. the noise sources are uncorrelated. We will look at the case of correlated noise sources later.

Figure 5: The equivalent noise of an arbitrary circuit with resistors and independent sources.

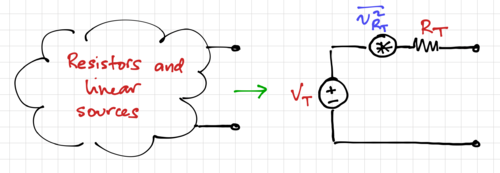
Extending these definitions to any arbitrary resistive circuit, we can determine the equivalent Thevenin or Norton equivalent circuit, as illustrated in Fig. 5, as well as the noise associated with the Thevenin resistance, $R_{T}$, as:

${\overline {v_{R_{T}}^{2}}}=4kTR_{T}\Delta f$

(14)