MOS Transistors

Analog circuits are generally sensitive to the nuances and details of transistor behavior, requiring precise and/or well-controlled voltages, currents, etc. Digital circuits, on the other hand, can have much larger margins of error due to their inherent noise margins and regenerative properties. Thus, we want to be able to model these nuances and details of transistor behavior in order to predict their effects on our circuits.

Transistor Models

Transistor models enable us to describe and predict the behavior of the circuits we build using these transistors by:

• Providing us with a window into the physical device characteristics (e.g. dimensions, material and device properties, etc.) and processes (e.g. drift/diffusion currents, tunneling, charge transfer, etc.), and
• Allowing us to perform easy to do "experiments" using simulators such as SPICE.

Levels of Abstraction

The complexity of transistor models can range from very simple models, such as modeling the transistor as a simple controlled switch, to very complex models such as BSIM models with hundreds of parameters.

We choose a model based on the questions we want answered. For example:

• For predicting the digital (boolean) functionality of a static CMOS gate, we can simply model the transistor as a controlled switch.
• However, if we want to predict the performance of the CMOS gate, we might need to model the ON current of the transistor as a current source in series with a switch.
• For high-precision analog circuits, we might need a BSIM model to predict the noise performance, settling time, stability, etc.

Note that "questions" that are more complicated require more complex and mathematically intensive models. Thus, it is best to match the model complexity to the problem or question we want answered. Further note that different models can be used to answer different questions at different stages of the design process.

The Square-Law MOSFET Model

Figure 1: The idealized NMOS transistor used to derive the square-law model.

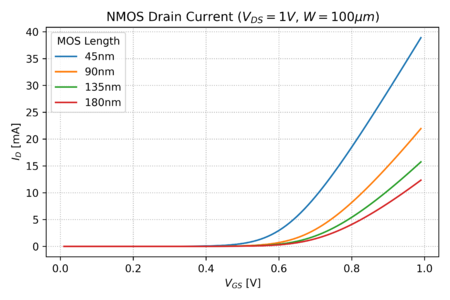
The widely known square-law MOSFET model is a good model for predicting the behavior of discrete and relatively large-sized transistors. It relates the drain saturation current to the gate-to-source voltage as:

$I_{D,\mathrm {sat} }={\frac {\mu _{n}C_{ox}}{2}}\cdot {\frac {W}{L}}\cdot \left(V_{GS}-V_{th}\right)^{2}$

(1)

Where $\mu _{n}$ is the electron mobility, $C_{ox}={\frac {\epsilon _{ox}}{t_{ox}}}$ is the gate-oxide capacitance per unit area, dependent on the permittivity and thickness of the gate oxide layer, and $V_{th}$ is the transistor threshold voltage.

However, the square-law model is inadequate for modeling short-channel behavior, since it is based on the following assumptions (not a complete list):

• The channel charge density is determined only by the vertical electric field due to $V_{GS}$.
• Drift velocity is set only by the lateral electric field due to $V_{DS}$.
• The mobility of electrons and holes are constant.
• There are no diffusion currents, and that $I_{D}=0$ when $V_{GS}<V_{th}$.

Submicron Transistors

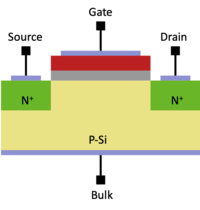
Due to manufacturing constraints and limitations, the structure of a deep submicron (with channel lengths of 90nm and below) transistors can differ quite dramatically from the idealized structure shown in Fig. 1. For an simple overview of the CMOS fabrication process, you can watch Silicon Run I (1996).

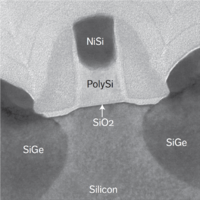
The cross section of modern MOSFETs with lengths of 90nm, 65nm, and 45nm are shown in Figs. 2, 3 and 4.

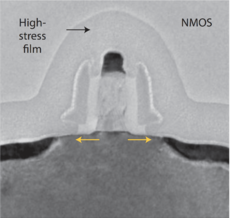Figure 2: Intel 90nm MOSFET with tensile channel strain.

Figure 3: Intel 65nm MOSFET using $\mathrm {SiO_{2}}$ as dielectric and polysilicon as the gate material.

Figure 4: Intel 45nm MOSFET with metal gate and hafnium-based dielectric..

Figure 5: The simplified cross-section of an advanced MOSFET.

As we can see, the cross-section of these real transistors are very different from the idealized transistor in Fig. 1. A simplified cross-section of a submicron transistor is shown in Fig. 5. A few noteworthy characteristics of advanced MOSFETs:

• Gate Electrode
• Ultra-thin Gate Dielectrics
• Source/Drain Engineering
• Short-Channel Effects
• Retrograde Doping
• Pocket Implants

Process Variations

In addition to these advanced MOSFET characteristics, the presence of run-to-run parameter variations, either systematic or random, adds another layer of uncertainty to the design process. These variations must be taken into consideration when designing analog circuits. One option is to use Monte Carlo simulations similar to our activity on passive element variations. However, for transistors with hundreds of parameters, these simulations would take a significant amount of time and computing resources even for relatively simple circuits.

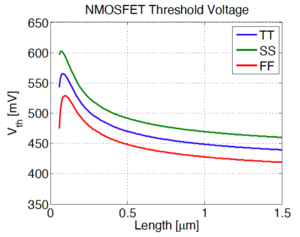
Corner analysis is an alternative to Monte Carlo simulation where the effects of individual device parameter variations are combined to determine device- or circuit-level performance variations. Worst-case and best-case performance variations are then identified as corners. For example, we can plot the speed of the NMOS and PMOS transistors as the threshold voltage, mobility, and oxide capacitance are varied. The worst cases, also known as the corner cases are shown in Fig. 6. These corners can then be translated back into the device parameter domain, e.g. the threshold voltage, to determine an acceptable range of values, depicted in Fig. 7.

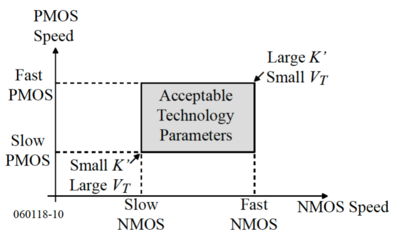Figure 6: MOSFET speed corners.

Figure 7: MOSFET threshold voltage corners.

Thus, instead of simulating random points, we can just simulate the device or circuit performance at these points to determine their corner behavior, e.g. the typical NMOS, typical PMOS case (TT corner), the fast NMOS, fast PMOS case (FF corner), the slow NMOS, slow PMOS case (SS corner), etc.

Short-Channel Effects

If our "simple" models are not sufficient, do we rely purely on simulators? No.

• Simulator models (e.g. BSIM) are not always based on real measurements
• Models inherently compromise accuracy for speed

We need to know the important short-channel effects so we know what to look for:

• The model might be wrong or might not include certain physical mechanisms

Threshold Voltage

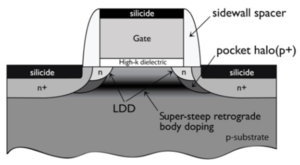
As the MOSFET channel length continues to scale, the distance between source and drain regions decreases. Due to this reduced distance, current can start to flow outside the designated channel area, i.e. deeper into the substrate. Thus, the gate voltage has less control of these currents since these currents are further away from the gate oxide, potentially leading to larger leakage currents. One way to prevent these sub-channel currents is to add halo or pocket implants, as shown in Fig. 8.

However, these implants result in the reverse short-channel effect, where the threshold voltage decreases as the transistor length increases, as shown in Figs. 9 and 10. Note that at shorter channel lengths, the halo implants are closer together, increasing the effective doping in the channel, thus increasing the threshold voltage. As the channel length is increased, the halo implants are pulled apart, increasing the channel region unaffected by the halo doping. This results in a reduction in threshold voltage.

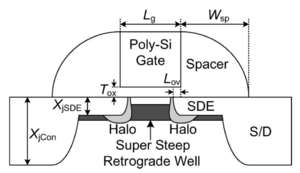Figure 8: A cross-section of a bulk MOSFET showing the halo implants.

Figure 9: The threshold voltage of a 45nm NMOS (PTM) transistor.

Figure 10: The threshold voltage of a "real" NMOS transistor.

Drain Current

For relatively small electric fields, the drift velocity of an electron is given by ${\vec {v}}_{d}=-\mu _{e}{\vec {E}}$. However, above a critical electric field, ${\vec {E_{c}}}$, the velocity starts to saturate, as seen in Fig. 11.

• Velocity Saturation

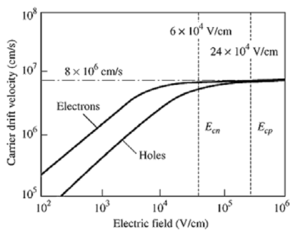Figure 11: Velocity saturation.

• Vertical Field Mobility Degradation
• The Subthreshold (Weak Inversion) Region
• The Moderate Inversion Region

Figure 12: The drain current vs. gate-source voltage of a 45nm NMOS (PTM) transistor.

Figure 13: The log of the drain current vs. gate-source voltage of a 45nm NMOS (PTM) transistor.

Output Resistance

• Channel Length Modulation (CLM)
• Drain-Induced Barrier Lowering (DIBL)
• Substrate Current Body Effect (SCBE)

Figure 14: The MOSFET drain current and output resistance mechanisms.

Transistor Models for Design

• Comprehensive models like BSIM:
  • Industry standard
  • Expertise needed to perform parameter extraction
  • 40-100+ parameters: requires many assumptions to be useful as a "hand calculation model"
  • Excellent for verification and modeling device variations
• Square-law, velocity-saturation model, small-signal models, or other "simple" models
  • Best to build intuition
  • Output resistance is the key to determine gain but is very hard to model
  • Does not model important regions such as moderate inversion

• Challenge: How to accurately design when hand analysis is way off?
• Answer: We will use the simulator as a "calculator" together with our "simple" models.

Further Reading

• M. T. Bohr and I. A. Young, CMOS Scaling Trends and Beyond, in IEEE Micro, vol. 37, no. 6, pp. 20-29, November/December 2017, doi: 10.1109/MM.2017.4241347. IEEExplore link
• Kim, Yong-bin, Challenges for Nanoscale MOSFETs and Emerging Nanoelectronics. Transactions on Electrical and Electronic Materials 11 (2010): 93-105. link