In general, the channel itself can add noise. This means that the channel adds an additional layer of uncertainty to our transmissions. Consider a channel with input symbols  , and output symbols
, and output symbols  . Note that the input and output alphabets do not need to have the same number of symbols. Given the noise in the channel, if we observe the output symbol
. Note that the input and output alphabets do not need to have the same number of symbols. Given the noise in the channel, if we observe the output symbol  , we are not sure which
, we are not sure which  was the input symbol.
was the input symbol.
We can then characterize the discrete channel as a set of probabilities  . If the probability distribution of the outputs depend on the current input, then the channel is memoryless. Let us consider the information we get from observing a symbol
. If the probability distribution of the outputs depend on the current input, then the channel is memoryless. Let us consider the information we get from observing a symbol  at the output of a discrete memoryless channel (DMC).
at the output of a discrete memoryless channel (DMC).
Definition

Figure 1: A noisy channel.
Given a probability model of the source, we have an a priori estimate  that symbol
that symbol  will be sent next. Upon observing
will be sent next. Upon observing  , we can revise our estimate to
, we can revise our estimate to  , as shown in Fig. 1. The change in information, or mutual information, is given by:
, as shown in Fig. 1. The change in information, or mutual information, is given by:
-
 |
|
(1)
|
Let's look at a few properties of mutual information. Expressing the equation above in terms of  :
:
-
 |
|
(2)
|
Thus, we can say:
-
 |
|
(3)
|
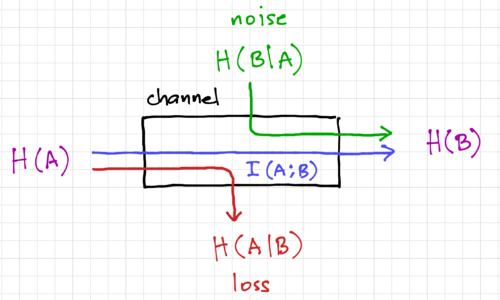
Figure 2: An information channel.
This is expected since, after observing  , the amount of uncertainty is reduced, i.e. we know a bit more about
, the amount of uncertainty is reduced, i.e. we know a bit more about  , and the most change in information we can get is when
, and the most change in information we can get is when  and
and  are perfectly correlated, with
are perfectly correlated, with  . Thus, we can think of mutual information as the average information conveyed across the channel, as shown in Fig. 2. From Bayes' Theorem, we have the property:
. Thus, we can think of mutual information as the average information conveyed across the channel, as shown in Fig. 2. From Bayes' Theorem, we have the property:
-
 |
|
(4)
|
Note that if  and
and  are independent, where
are independent, where  and
and  , then:
, then:
-
 |
|
(5)
|
We can get the average mutual information over all the input symbols as:
-
 |
|
(6)
|
Similarly, for all the output symbols:
-
 |
|
(7)
|
For both input and output symbols, we get:
-
 |
|
(8)
|
Non-Negativity of Mutual Information
To show the non-negativity of mutual information, let us use Jensen's Inequality, which states that for a convex function,  :
:
-
 |
|
(9)
|
Using the fact that  is convex, and applying this to our expression for mutual information, we get:
is convex, and applying this to our expression for mutual information, we get:
-
 |
|
(10)
|
Note that  when
when  and
and  are independent.
are independent.
Conditional and Joint Entropy
Given  and
and  , and their entropies:
, and their entropies:
-
 |
|
(11)
|
-
 |
|
(12)
|
Conditional Entropy
The conditional entropy is a measure of the average uncertainty about  when
when  is known, and we can define it as:
is known, and we can define it as:
-
 |
|
(13)
|
And similarly,
-
 |
|
(14)
|
Joint Entropy
If we extend the definition of entropy to two (or more) random variables,  and
and  , we can define the joint entropy of
, we can define the joint entropy of  and
and  as:
as:
-
 |
|
(15)
|
Expanding expression for joint entropy, and using  we get:
we get:
-
 |
|
(16)
|
If we instead used  , we would get the alternative expression:
, we would get the alternative expression:
-
 |
|
(17)
|
We can then expand our expression for  as:
as:
-
 |
|
(18)
|
We can then think of mutual information as the reduction in uncertainty due to another random variable. The above relationships between mutual information and the entropies are illustrated in Fig. 2. Note that  since
since  . We can then write:
. We can then write:
-
 |
|
(19)
|
Thus, we can think of entropy as self-information.
Channel Capacity
The maximum amount of information that can be transmitted through a discrete memoryless channel, or the channel capacity, with units bits per channel use, can then be thought of as the maximum mutual information over all possible input probability distributions:
-
 |
|
(20)
|
Or equivalently, we need to choose  such that we maximize
such that we maximize  . Since:
. Since:
-
 |
|
(21)
|
And if we are using the channel at its capacity, then for every  :
:
-
 |
|
(22)
|
Thus, we can maximize channel use by maximizing the use for each symbol independently. From the definition of mutual information and from the Gibbs inequality, we can see that:
-
 |
|
(23)
|
Where  and
and  are the number of symbols in
are the number of symbols in  and
and  respectively. Thus, the channel capacity of a channel is limited by the logarithm of the number of distinguishable symbols at its input (or output).
respectively. Thus, the channel capacity of a channel is limited by the logarithm of the number of distinguishable symbols at its input (or output).
Sources
- Tom Carter's notes on Information Theory
- Dan Hirschberg's notes on Data Compression
- Lance Williams' notes on Geometric and Probabilistic Methods in Computer Science
References
















































