Resonance

Series Resonant Circuits

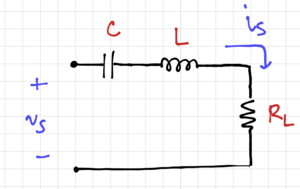
Figure 1: A series RLC circuit.

Consider the series resonant RLC circuit shown in Fig. 1. We can calculate the total impedance seen by the source $v_{S}$, as:

$Z=R_{L}+j\omega L+{\frac {1}{j\omega C}}$

(1)

Combining the imaginary terms of the impedance, we get:

$Z=R_{L}+j\left(\omega L-{\frac {1}{\omega C}}\right)$

(2)

We can see that the imaginary component of the impedance becomes zero at the resonant frequency, $\omega _{0}$, equal to:

$\omega _{0}={\frac {1}{\sqrt {LC}}}$

(3)

Note that the cancellation is narrowband, since perfect cancellation occurs only at a single frequency. Thus, from the point of view of the voltage source $v_{S}$, the impedance $Z$ is purely real. We can then calculate the current, $i_{S}$ as:

$i_{S}={\frac {v_{S}}{R_{L}}}$

(4)

We then use this current to calculate the voltage across the inductor and capacitor:

$v_{L}=i_{S}\cdot j\omega _{0}L={\frac {v_{S}}{R_{L}}}\cdot j\omega _{0}L=v_{S}\cdot jQ_{S}$

(5)

$v_{C}=i_{S}\cdot {\frac {1}{j\omega _{0}C}}=-{\frac {v_{S}}{R_{L}}}\cdot j{\frac {1}{\omega _{0}C}}=-v_{S}\cdot jQ_{S}$

(6)

Where $Q_{S}$ is the series circuit quality factor:

$Q_{S}={\frac {\omega _{0}L}{R_{L}}}={\frac {1}{\omega _{0}R_{L}C}}$

(7)

Note that:

1. For small values of $R_{L}$ results in large values of $Q_{S}$, leading to large voltages across the inductor and capacitor.
2. The voltage across the inductor is exactly $180^{\circ }$ out of phase with the capacitor voltage, thus cancelling each other out.

Parallel Resonant Circuits

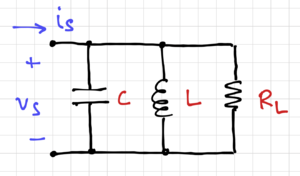
Figure 2: A parallel RLC circuit.

For the parallel resonant RLC circuit in Fig. 2, the total admittance seen by the current source is:

$Y={\frac {1}{R_{L}}}+j\omega C+{\frac {1}{j\omega L}}={\frac {1}{R_{L}}}+j\left(\omega C-{\frac {1}{\omega L}}\right)$

(8)

The admittance becomes purely real at the resonant frequency, $\omega _{0}={\tfrac {1}{\sqrt {LC}}}$. Once again, we can calculate the voltage across $R_{L}$ as:

$v_{S}=i_{S}\cdot R_{L}$

(9)

Thus, the currents through the inductor and capacitor can be expressed as:

$i_{L}={\frac {v_{S}}{j\omega _{0}L}}=-i_{S}\cdot j{\frac {R_{L}}{\omega _{0}L}}=-i_{S}\cdot jQ_{P}$

(10)

$i_{C}=v_{S}\cdot j\omega _{0}C=i_{S}\cdot j\omega _{0}R_{L}C=i_{S}\cdot jQ_{P}$

(11)

Where the parallel quality factor, $Q_{P}$ is equal to:

$Q_{P}={\frac {R_{L}}{\omega _{0}L}}=\omega _{0}R_{L}C$

(12)

Similar to the series resonant circuit, we see that even though the currents across the reactances cancel out, the individual currents could be very large.