Difference between revisions of "Chebyshev Filters"
| Line 2: | Line 2: | ||
== The Chebyshev Type-I Low-Pass Filter == | == The Chebyshev Type-I Low-Pass Filter == | ||
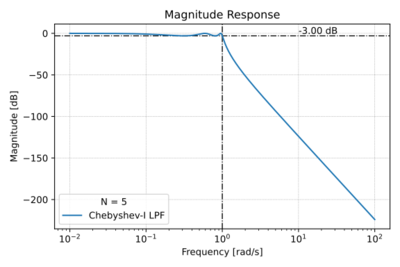
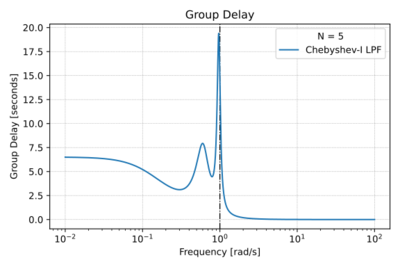
| − | Chebyshev Type-I filters are also ''all-pole filters'', with poles of the normalized (<math>\omega_0 = 1\,\mathrm{\tfrac{rad}{s}}</math>) filter located on an ellipse inside the unit circle. This arrangement of poles results in (1) a shorter transition band, and therefore a steeper roll-off compared to the Butterworth low-pass filter of the same order, (2) poorer group delay characteristics, and (3) ripples in the pass-band. By allowing larger ripples in the pass-band, we get: (1) a narrower transition band, and hence sharper cut-off, (2) higher Q poles, and (3) more degradation in the phase response. | + | Chebyshev Type-I filters are also ''all-pole filters'', with poles of the normalized (<math>\omega_0 = 1\,\mathrm{\tfrac{rad}{s}}</math>) filter located on an ellipse inside the unit circle, as shown in Fig. 1. This arrangement of poles results in (1) a shorter transition band, and therefore a steeper roll-off compared to the Butterworth low-pass filter of the same order, shown in Fig. 2, (2) poorer group delay characteristics as depicted in Figs. 3 and 4, and (3) ripples in the pass-band also seen in Fig. 2. By allowing larger ripples in the pass-band, we get: (1) a narrower transition band, and hence sharper cut-off, (2) higher Q poles, and (3) more degradation in the phase response. |
{| | {| | ||
Revision as of 00:35, 16 March 2021
Chebyshev filters come in two flavors: the Type-I and Type-II.
The Chebyshev Type-I Low-Pass Filter
Chebyshev Type-I filters are also all-pole filters, with poles of the normalized () filter located on an ellipse inside the unit circle, as shown in Fig. 1. This arrangement of poles results in (1) a shorter transition band, and therefore a steeper roll-off compared to the Butterworth low-pass filter of the same order, shown in Fig. 2, (2) poorer group delay characteristics as depicted in Figs. 3 and 4, and (3) ripples in the pass-band also seen in Fig. 2. By allowing larger ripples in the pass-band, we get: (1) a narrower transition band, and hence sharper cut-off, (2) higher Q poles, and (3) more degradation in the phase response.
The Chebyshev Type-I magnitude response is given by:
-
(1)
-
Where is the cut-off frequency, is the ripple factor with ripple in dB, and are solutions to the Chebyshev differential equation:
-
(2)
-
For a normalized filter, or , the poles of the Chebyshev Type-I low-pass filter are the roots of . In practice, instead of solving this equation directly, we can easily get the roots (and hence the poles) of the filter magnitude response using tools such as Python or Matlab.