Difference between revisions of "CoE 197U The MOS Switch"
| Line 18: | Line 18: | ||
== Digital Transistor Operation == | == Digital Transistor Operation == | ||
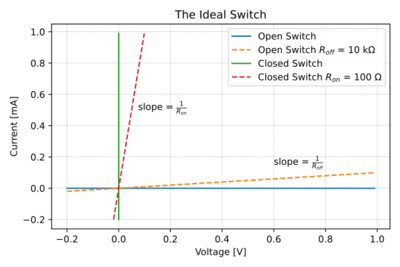
| − | In digital circuits, the inputs and outputs are ideally limited to two voltage levels, usually <math>V_{DD}</math> and ground. | + | In digital circuits, the inputs and outputs are ideally limited to two voltage levels, usually <math>V_{DD}</math> or logic '''1''' and ground or logic '''0'''. Fig. 2 shows the output characteristic of an NMOS transistor. Note that for large <math>V_{GS}</math>, e.g. 1V, the <math>V_{DS}</math> vs. <math>I_D</math> characteristic of the NMOS transistor looks very much like a closed switch with a low series resistance, as seen in Fig. 3. |
| − | |||
| − | Fig. 2 shows the output characteristic of an NMOS transistor. | ||
{| | {| | ||
|[[File:NMOS output tt.png|thumb|400px|Figure 2: The 45nm NMOS PTM<ref name="asu-ptm">Arizona State University Predictive Technology Models (PTM) [http://ptm.asu.edu/ website]</ref> output characteristics.]] | |[[File:NMOS output tt.png|thumb|400px|Figure 2: The 45nm NMOS PTM<ref name="asu-ptm">Arizona State University Predictive Technology Models (PTM) [http://ptm.asu.edu/ website]</ref> output characteristics.]] | ||
| + | |[[File:Ideal switch.svg|thumb|400px|Figure 3: The ideal switch V-I characteristics.]] | ||
|- | |- | ||
|} | |} | ||
| Line 29: | Line 28: | ||
=== The Ideal Switch === | === The Ideal Switch === | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
=== The Switch Model of a Transistor === | === The Switch Model of a Transistor === | ||
Revision as of 10:31, 10 March 2021
Contents
Levels of Abstraction
As integrated circuits continue to increase in complexity and sophistication, the amount of information and information processing needed to design, fabricate, and test these ICs also increase. Without a way to organize this information, engineers can be easily overwhelmed. One strategy is to define levels of abstraction, where we partition the information, and use only the components needed for a particular task. This strategy can then be used to create models appropriate for a certain objective.
We create models to allow us to predict the behavior of a circuit or system. One approach we can take is to model a whole system using transistor models, e.g. BSIM[1] models, with hundreds of parameters per transistor. The amount of computing resources needed for systems with millions of transistors could render this approach impractical.
In most cases, the overall functionality of a digital system is determined by the system architecture and organization, e.g. is it an adder, or a multiplier, or a microprocessor? At this level, we do not really need to know transistor-level details such as the threshold voltage or the thickness of the gate oxide. Thus, we can abstract away the unneeded information, and retain only the information needed to accomplish the task. By reducing the complexity of the transistor model, we can significantly reduces the amount of computation needed to verify the functionality of the digital system. However, if we want to predict or determine the leakage power consumption of the system, then we need to take into account the transistor threshold voltages, leading to a different simulation strategy and transistor model abstraction.
Fig. 1 shows an example of how a system can be seen from different levels of abstractions or viewpoints, from the system-level, to the RTL- or functional-level, the gate-level, the transistor-level, and the physical-level. Different models with varying sophistication and complexity can be used at the different levels, depending on the design or verification objective. In general, more information about the transistors are added as we get closer to the physical-level.
 Figure 1: Levels of abstraction[2]. |
For example, at the system-level, we may be interested in overall functionality of the IC and how it interfaces with other components or systems. At the register transfer level (RTL), we might be concerned with the system architecture, e.g. how it uses resources such as memory and interconnect to implement its function. Then each function could be examined in more detail at the gate-level, we can evaluate gate fan-in and fan-out, logic depth, etc. At the transistor-level, we can look at specific timing-, voltage- and current-related parameters such as rise times, propagation delays, voltage and current spikes, active and leakage power, etc. The physical-layer view can show us the effect of the layout and location of transistors and transistor groups, allowing us to determine the effects of parasitic elements and other layout related phenomena.
To understand the functionality of digital systems, let us first consider the functionality and performance of the simplest of all digital CMOS gates -- the inverter. We will see that we can easily extend these to more complex gates. Since we only want to look at CMOS inverters from a digital point of view, let us see if we can create a simple model for our transistors that is appropriate for this task.
Digital Transistor Operation
In digital circuits, the inputs and outputs are ideally limited to two voltage levels, usually or logic 1 and ground or logic 0. Fig. 2 shows the output characteristic of an NMOS transistor. Note that for large , e.g. 1V, the vs. characteristic of the NMOS transistor looks very much like a closed switch with a low series resistance, as seen in Fig. 3.
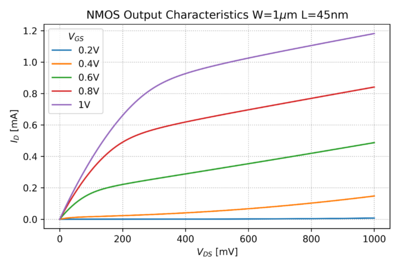 Figure 2: The 45nm NMOS PTM[3] output characteristics. |