Difference between revisions of "Integrated Capacitors"
| Line 7: | Line 7: | ||
{{NumBlk|::|<math>C = \frac{\epsilon A}{t} = \frac{\epsilon}{t}\cdot w\cdot \ell = C_\mathrm{layer}\cdot w\cdot \ell</math>|{{EquationRef|1}}}} | {{NumBlk|::|<math>C = \frac{\epsilon A}{t} = \frac{\epsilon}{t}\cdot w\cdot \ell = C_\mathrm{layer}\cdot w\cdot \ell</math>|{{EquationRef|1}}}} | ||
| − | Where <math>C_\mathrm{layer} = \tfrac{\epsilon}{t}</math> is the capacitance density of a particular layer, <math>\epsilon</math> is the permittivity of the dielectric or insulating material, <math>t</math> is the thickness of the dielectric, and <math>A = w\cdot \ell</math> is the overlap area of the parallel-plate. | + | Where <math>C_\mathrm{layer} = \tfrac{\epsilon}{t}</math> is the capacitance density, or capacitance per unit area, of a particular layer, <math>\epsilon</math> is the permittivity of the dielectric or insulating material, <math>t</math> is the thickness of the dielectric, and <math>A = w\cdot \ell</math> is the overlap area of the parallel-plate. |
=== Parasitic Capacitances === | === Parasitic Capacitances === | ||
| Line 23: | Line 23: | ||
{| | {| | ||
|[[File:Aparicio 4.png|thumb|300px|Figure 2: Stacked horizontal parallel-plates<ref name="aparicio2002">Aparicio, Roberto and Hajimiri, Ali, ''Capacity limits and matching properties of integrated capacitors'', 2002, IEEE Journal of Solid-State Circuits, 37 (3). pp. 384-393. ISSN 0018-9200 (alternative [https://authors.library.caltech.edu/6776/1/APAieeejssc02a.pdf pdf] link)</ref>.]] | |[[File:Aparicio 4.png|thumb|300px|Figure 2: Stacked horizontal parallel-plates<ref name="aparicio2002">Aparicio, Roberto and Hajimiri, Ali, ''Capacity limits and matching properties of integrated capacitors'', 2002, IEEE Journal of Solid-State Circuits, 37 (3). pp. 384-393. ISSN 0018-9200 (alternative [https://authors.library.caltech.edu/6776/1/APAieeejssc02a.pdf pdf] link)</ref>.]] | ||
| − | |[[File:Aparicio 1.png|thumb| | + | |[[File:Aparicio 1.png|thumb|350px|Figure 3: Vertical parallel-plates<ref name="aparicio2002"/>.]] |
| − | |[[File:Aparicio 3.png|thumb| | + | |[[File:Aparicio 3.png|thumb|350px|Figure 4: Combining vertical and horizontal parallel-plates<ref name="aparicio2002"/>.]] |
|- | |- | ||
|} | |} | ||
Revision as of 06:11, 22 September 2020
Similar to resistors, in a CMOS process optimized for digital circuits, capacitances are treated as parasitic devices that degrade the performance of digital circuits, except in specialized cases such as memory circuits. However, in analog design, we often need capacitors with very well-controlled capacitance values.
Contents
Capacitor Geometries
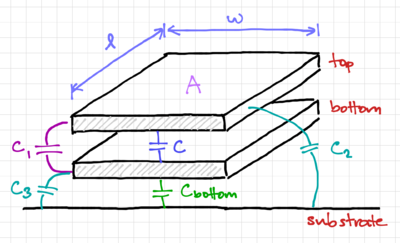
The parallel-plate capacitance of the structure shown in Fig. 1, is given by:
-
(1)
-
Where is the capacitance density, or capacitance per unit area, of a particular layer, is the permittivity of the dielectric or insulating material, is the thickness of the dielectric, and is the overlap area of the parallel-plate.
Parasitic Capacitances
In addition to the main parallel-plate capacitance, , we would get the following parasitic capacitances:
- A bottom plate parasitic capacitance, , between the bottom plate and the substrate.
- Perimeter-dependent fringing capacitances, due to the fringing electric fields between the:
- top plate and bottom plate, , resulting in an increase in the main capacitance predicted by the parallel-plate expression in Eq. 1,
- top plate and substrate, , adding a top plate parasitic capacitance, and
- bottom plate and substrate, , again adding to the capacitance predicted by our parallel-plate formula.
Note that it is much harder to model and predict the capacitance due to the non-uniform fringing electric fields. We can reduce the effects of the fringing fields by making the main capacitance much larger than the parasitic fringing capacitances by minimizing the perimeter of the parallel-plate structure.
Alternative Parallel-Plate Structures
To support the increasing complexity of digital circuits, additional routing layers have been made available in advanced CMOS processes. This increase in metal layers opens up the possibility of using multiple layers, shown in Fig. 2, or even horizontal electric fields, in addition to vertical fields, as seen in Figs. 3 and 4, in creating very high-density, and well controlled, capacitor structures.
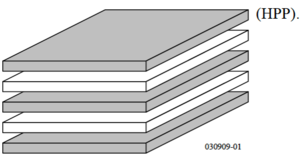 Figure 2: Stacked horizontal parallel-plates[1]. |
 Figure 3: Vertical parallel-plates[1]. |
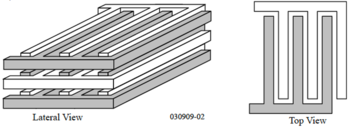 Figure 4: Combining vertical and horizontal parallel-plates[1]. |