Probability review for warm up

Probability Review

In this section, let's go through a quick review about probability theory. The best way to refresh ourselves is to read a few notes and go straight to problem exercises. From your EEE 137 we can summarize probability as a mathematical term which we use to investigate properties of mathematical models of chance phenomena. It is also a generalized notion of weights whereby we weigh events to see how likely they are to occur. In most cases probability is dependent on the relative frequency of events, while some look at fractions based on sets. Let's review some important properties and definitions then proceed immediately to practice exercises.

Basic Properties of Probability

Suppose we have events $A$ and $B$ which are subsets of a sample space $S$ (i.e., $A,B\subset S$ ). Let $P(A)$ be the probability that event $A$ happens, and $P(B)$ be the probability that event $B$ happens. Then some of the basic properties follow:

1. $0\leq P(A)\leq 1$ and $0\leq P(B)\leq 1$
2. $P(S)=1$ and $P(\varnothing )=0$. The $\varnothing$ is the null or empty set.
3. $P(A\cap B)=P(A)+P(B)$ if and only if $A$ and $B$ are disjoint.
4. $P(A-B)=P(A)-P(B)$ if $B\subseteq A$ and vice versa.
5. $P({\bar {A}})=1-P(A)$ and $P({\bar {B}})=1-P(B)$
6. $P(A)\leq P(B)$ whenever $A\subseteq B$ and vice versa.
7. $P(A\cup B)=P(A)+P(B)-P(A\cap B)$. This can be extended to $N$ sets or variables. This one is left as an exercise for you.
8. Let's say $C=\{E_{1},E_{2},E_{3}...,E_{n}\}$ is a partition of $S$ then $\sum _{j=1}^{n}P(E_{j})=1$.

Principle of Symmetry

Let $S$ be a finite sample space with outcomes or events $\{E_{1},E_{2},E_{3},...,E_{n}\}$ which all $E_{i}$ are physically identical or objects having the same properties and characteristics. In this case we have:

$P(E_{1})=P(E_{2})=P(E_{3})=...=P(E_{n})$.

Subjective Probabilities

These are often expressed in terms of odds. For example, suppose a betting site is offering odds of $x$ to $y$ on Team Secret beating Team TSM. This means out of the total $x+y$ equally valued coins, the better is willing to bet $x$ of them that Team Secret beats Team TSM. So if the outcome $s$ is the event that Team Secret beats Team TSM then we have:

$P(s)={\frac {x}{x+y}}$

Relative Frequency

Suppose we are monitoring a particular outcome $x$ and we observe that $x$ occurs in $r$ out of $n$ experiments (or repetitions). We define the relative frequency of $x$ based on $n$ experiments as:

$P(x)={\frac {r}{n}}$

Conditional Probability

Figure 1: Simple Venn diagram showing the fractional parts for computing $P(A|B)$

In a nutshell, conditional probability is to gain in information about an event that leads to a change in its probability. Suppose an event $A$ happens with probability $P(A)$. However, when event $B$ happens, this influences the probability of $A$ such that we have $P(A|B)$ as the conditional probability of $A$ happening given $B$ occurred. Mathematically we know this as:

$P(A|B)={\frac {P(A\cap B)}{P(B)}}$

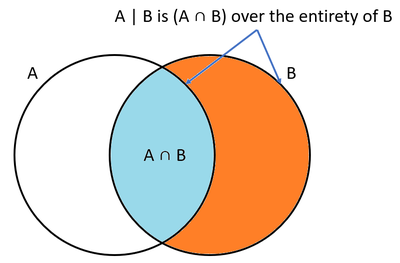
Figure 1 shows a Venn diagram that can visualize this. The $P(A|B)$ is the relative probability of event $A$ happening with respect to event $B$ happening. Therefore, it justifies that we first need to get $P(A\cap B)$ then dividing this by $P(B)$. It's just a matter of shifting the scope of event $A$ happening with respect to the entire space $S$ to the scope of event $A$ happening with respect to the space of event $B$. We can rearrange the equation to get:

$P(A\cap B)=P(A|B)P(B)$

We can extend this concept to three or more sets. For example, if $A$, $B$, and $C$ are some events in a sample space, then we can compute the intersection of all events as:

$P(A\cap B\cap C)=P(C|A\cap B)P(B|A)P(A)$

Figure 2: Simple partition example. The entire space $S$ is cut into different $E_{i}$ parts. The event $A$ is a subset of the space and it constitutes different fractions of $E_{i}$ components.

Here's another interesting formula: Suppose we have a partition set $Y=\{E_{1},E_{2},E_{3},...E_{n}\}$ of some sample space $S$ with each $P(E_{i})\neq 0$. In other words, we just cut the sample space $S$ into several partitions. Let event $A\ \epsilon \ Y$. In other words, event $A$ is just a part of the partition $Y$. We have:

$P(A)=\sum _{i=1}^{n}P(A|E_{i})P(E_{i})$

Figure 2 visualizes this formula. The entire space is $S$ and we cut it into several $E_{i}$ components. Suppose event $A$ is also part of the entire space $S$, then it's simply the sum of all $P(E_{i}\cap A)=P(A|E_{i})P(E_{i})$ components. You might wonder why the summation is from $i=1$ up to $i=n$ when we could just get the probabilities where it only matters? You are correct to think that we only need to get those that have a contribution to $P(A)$ but the equation is generalized to include all partitions. For example, $P(E_{6}\cap A)=0$ because event $E_{6}$ and event $A$ can never happen. So it's okay to generalize the formula to include all events even when their intersections don't happen at all.

Bayes' Theorem

Bayes' theorem is an extension of the conditional probability. Consider again that we have events $A$ and $B$ of some sample space $S$. Bayes' theorem states that:

$P(A|B)={\frac {P(A)P(B|A)}{P(B)}}$

We can rearrange it to be aesthetically symmetric:

$P(A|B)P(B)=P(B|A)P(A)$

Bayes' theorem can be very useful to describe the probability of an event that is based on prior knowledge of conditions that may be related to the event.

Independence

In ordinary language, independence usually means that two experiences are completely separate. If an event happens it has no effect on the other. Given events $A$ and $B$ are independent, then the following should hold true:

1. $P(A\cap B)=P(A)P(B)$
2. $P(A|B)=P(A)$
3. $P(B|A)=P(B)$

Random Variables

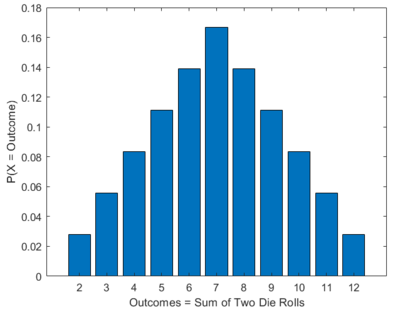
A discrete random variable is a variable whose value is uncertain. In practice this random variable is just a mapping of different outcomes and their respective probabilities of occurring associated to a single variable only. We usually denote random variables with capital letters, just like $X$. For example, let a discrete random variable $X$ represent the scenarios the sum of two independent die rolls. The set of possible outcomes would be:

$\{2,3,4,5,6,7,8,9,10,11,12\}$

Now, each outcome would have some probability associated with it. The list below shows the pair-wise mapping. We'll leave it as an exercise for you to determine how to get these probabilities.

Bar graph for the probability distribution of the sum of two die rolls.

• $P(X=2)={\frac {1}{36}}$
• $P(X=3)={\frac {1}{18}}$
• $P(X=4)={\frac {1}{12}}$
• $P(X=5)={\frac {1}{9}}$
• $P(X=6)={\frac {5}{36}}$
• $P(X=7)={\frac {1}{6}}$
• $P(X=8)={\frac {5}{36}}$
• $P(X=9)={\frac {1}{9}}$
• $P(X=10)={\frac {1}{12}}$
• $P(X=11)={\frac {1}{18}}$
• $P(X=12)={\frac {1}{36}}$

The mapping between the outcomes and their corresponding probabilities is called a probability distribution. It describes the chances of the random variable to be one of the outcomes. It is common to visualize discrete random variables with bar graphs. Figure 3 shows the probability distribution of our two die rolls example.