Probability review for warm up

Probability Review

In this section, let's go through a quick review about probability theory. The best way to refresh ourselves is to read a few notes and go straight to problem exercises. From your EEE 137 we can summarize probability as a mathematical term which we use to investigate properties of mathematical models of chance phenomena. It is also a generalized notion of weights whereby we weigh events to see how likely they are to occur. In most cases probability is dependent on the relative frequency of events, while some look at fractions based on sets. Let's review some important properties and definitions then proceed immediately to practice exercises.

Basic Properties of Probability

Suppose we have events $A$ and $B$ which are subsets of a sample space $S$ (i.e., $A,B\subset S$ ). Let $P(A)$ be the probability that event $A$ happens, and $P(B)$ be the probability that event $B$ happens. Then some of the basic properties follow:

1. $0\leq P(A)\leq 1$ and $0\leq P(B)\leq 1$
2. $P(S)=1$ and $P(\varnothing )=0$. The $\varnothing$ is the null or empty set.
3. $P(A\cup B)=P(A)+P(B)$ if and only if $A$ and $B$ are disjoint.
4. $P(A-B)=P(A)-P(B)$ if $B\subseteq A$ and vice versa.
5. $P({\bar {A}})=1-P(A)$ and $P({\bar {B}})=1-P(B)$
6. $P(A)\leq P(B)$ whenever $A\subseteq B$ and vice versa.
7. $P(A\cup B)=P(A)+P(B)-P(A\cap B)$. This can be extended to $N$ sets or variables. This one is left as an exercise for you.
8. Let's say $C=\{E_{1},E_{2},E_{3}...,E_{n}\}$ is a partition of $S$ then $\sum _{j=1}^{n}P(E_{j})=1$.

Principle of Symmetry

Let $S$ be a finite sample space with outcomes or events $\{E_{1},E_{2},E_{3},...,E_{n}\}$ which all $E_{i}$ are physically identical or objects having the same properties and characteristics. In this case we have:

$P(E_{1})=P(E_{2})=P(E_{3})=...=P(E_{n})$.

Subjective Probabilities

These are often expressed in terms of odds. For example, suppose a betting site is offering odds of $x$ to $y$ on Team Secret beating Team TSM. This means out of the total $x+y$ equally valued coins, the better is willing to bet $x$ of them that Team Secret beats Team TSM. So if the outcome $s$ is the event that Team Secret beats Team TSM then we have:

$P(s)={\frac {x}{x+y}}$

Relative Frequency

Suppose we are monitoring a particular outcome $x$ and we observe that $x$ occurs in $r$ out of $n$ experiments (or repetitions). We define the relative frequency of $x$ based on $n$ experiments as:

$P(x)={\frac {r}{n}}$

Conditional Probability

Figure 1: Simple Venn diagram showing the fractional parts for computing $P(A|B)$

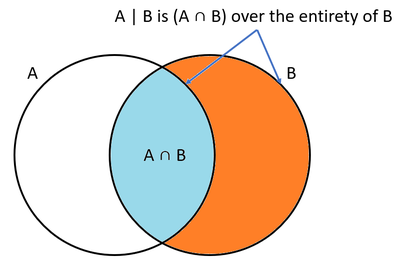
In a nutshell, conditional probability is to gain in information about an event that leads to a change in its probability. Suppose an event $A$ happens with probability $P(A)$. However, when event $B$ happens, this influences the probability of $A$ such that we have $P(A|B)$ as the conditional probability of $A$ happening given $B$ occurred. Mathematically we know this as:

$P(A|B)={\frac {P(A\cap B)}{P(B)}}$

Figure 1 shows a Venn diagram that can visualize this. The $P(A|B)$ is the relative probability of event $A$ happening with respect to event $B$ happening. Therefore, it justifies that we first need to get $P(A\cap B)$ then dividing this by $P(B)$. It's just a matter of shifting the scope of event $A$ happening with respect to the entire space $S$ to the scope of event $A$ happening with respect to the space of event $B$. We can rearrange the equation to get:

$P(A\cap B)=P(A|B)P(B)$

We can extend this concept to three or more sets. For example, if $A$, $B$, and $C$ are some events in a sample space, then we can compute the intersection of all events as:

$P(A\cap B\cap C)=P(C|A\cap B)P(B|A)P(A)$

Figure 2: Simple partition example. The entire space $S$ is cut into different $E_{i}$ parts. The event $A$ is a subset of the space and it constitutes different fractions of $E_{i}$ components.

Here's another interesting formula: Suppose we have a partition set $Y=\{E_{1},E_{2},E_{3},...E_{n}\}$ of some sample space $S$ with each $P(E_{i})\neq 0$. In other words, we just cut the sample space $S$ into several partitions. Let event $A\ \epsilon \ Y$. In other words, event $A$ is just a part of the partition $Y$. We have:

$P(A)=\sum _{i=1}^{n}P(A|E_{i})P(E_{i})$

Figure 2 visualizes this formula. The entire space is $S$ and we cut it into several $E_{i}$ components. Suppose event $A$ is also part of the entire space $S$, then it's simply the sum of all $P(E_{i}\cap A)=P(A|E_{i})P(E_{i})$ components. You might wonder why the summation is from $i=1$ up to $i=n$ when we could just get the probabilities where it only matters? You are correct to think that we only need to get those that have a contribution to $P(A)$ but the equation is generalized to include all partitions. For example, $P(E_{6}\cap A)=0$ because event $E_{6}$ and event $A$ can never happen. So it's okay to generalize the formula to include all events even when their intersections don't happen at all.

Bayes' Theorem

Bayes' theorem is an extension of the conditional probability. Consider again that we have events $A$ and $B$ of some sample space $S$. Bayes' theorem states that:

$P(A|B)={\frac {P(A)P(B|A)}{P(B)}}$

We can rearrange it to be aesthetically symmetric:

$P(A|B)P(B)=P(B|A)P(A)$

Bayes' theorem can be very useful to describe the probability of an event that is based on prior knowledge of conditions that may be related to the event.

Independence

In ordinary language, independence usually means that two experiences are completely separate. If an event happens it has no effect on the other. Given events $A$ and $B$ are independent, then the following should hold true:

1. $P(A\cap B)=P(A)P(B)$
2. $P(A|B)=P(A)$
3. $P(B|A)=P(B)$

Random Variables

A discrete random variable is a variable whose value is uncertain. In practice this random variable is just a mapping of different outcomes and their respective probabilities of occurring associated to a single variable only. We usually denote random variables with capital letters, just like $X$. For example, let a discrete random variable $X$ represent the scenarios the sum of two independent die rolls. The set of possible outcomes would be:

$\{2,3,4,5,6,7,8,9,10,11,12\}$

Now, each outcome would have some probability associated with it. The list below shows the pair-wise mapping. We'll leave it as an exercise for you to determine how to get these probabilities.

Figure 3: Bar graph for the probability distribution of the sum of two die rolls.

• $P(X=2)={\frac {1}{36}}$
• $P(X=3)={\frac {1}{18}}$
• $P(X=4)={\frac {1}{12}}$
• $P(X=5)={\frac {1}{9}}$
• $P(X=6)={\frac {5}{36}}$
• $P(X=7)={\frac {1}{6}}$
• $P(X=8)={\frac {5}{36}}$
• $P(X=9)={\frac {1}{9}}$
• $P(X=10)={\frac {1}{12}}$
• $P(X=11)={\frac {1}{18}}$
• $P(X=12)={\frac {1}{36}}$

The mapping between the outcomes and their corresponding probabilities is called a probability distribution. It describes the chances of the random variable to be one of the outcomes. It is common to visualize discrete random variables with bar graphs. Figure 3 shows the probability distribution of our two die rolls example. It is more convenient to write $P(X=x_{i})=p(x_{i})$.

Expectations and Variances

Whenever we are come across a random variable, we are always interested in the characteristics of the distribution. Particularly on expectation and variance. The expectation of a random variable $X$ is:

$E(X)=\sum _{j=1}^{n}p_{j}x_{j}$

The expectation is simply a linear combination of the outcome value and the probability of that value to occur. If you think about it carefully, we are trying to find what is the "expected" tendency of the value of the random variable. We also call the expectation as the mean of the random variable. We also denote the mean using the $\mu$ symbol. If the outcomes are equiprobable, then we arrive at the well known "average" equation. For example, if the random variable $X$ has $n$ outcomes and they are uniformly distributed (i.e., $p_{j}={\frac {1}{n}}$) then the expectation equation translates to:

$E(X)={\frac {1}{n}}\sum _{j=1}^{n}x_{j}$

Variance is a measure of how much can the random variable $X$ deviate from the mean $\mu$. We write the variance as:

${\textrm {Var}}(X)=E((X-\mu )^{2})=\sum _{j=1}^{n}(x_{j}-\mu )^{2}p_{j}$

We usually write variance with $\sigma ^{2}$. Take note that the units of variance is in ${\textrm {units}}^{2}$. We sometimes use the term standard deviation instead so that we get the original units. This is:

$\sigma (X)={\sqrt {{\textrm {Var}}(X)}}$

Different Distributions of Discrete Random Variables

Sometimes it's useful to recognize some well-established distributions for random variables. Here are a few examples.

Uniform Distribution

Given some random variable $X$ with $n$ unique outcomes, the probability distribution is:

$p(x_{1})=p(x_{2})=p(x_{3})=...=p(x_{n})$

We can compute the mean and variance using the appropriate equations mentioned earlier.

Binomial Distribution

Binomial random variables is an experiment with exactly two possible outcomes. For example, if we flip a fair coin ($p=0.5$), what is the probability of getting a head? The binomial distribution describes the problem: What is the probability of exactly $k$ heads in a sequence of $n$ independent trials. In equation form we write this as:

$p(k)={n \choose k}p^{k}(1-p)^{n-k}$

Take note that the function is dependent on $n$ trials and the probability $p$ where we get a success. Binomial distribution is also known as Bernoulli trials. Conveniently, the mean is $\mu =np$ and the variance is $\sigma ^{2}=np(1-p)$.

Poisson Distribution

The Poisson distribution is an extension of the binomial distribution but for rare events. The assumptions for the Poisson distribution include $n\rightarrow \infty$ and $p\rightarrow 0$. The number of trials need to be large and the event that we are looking into needs to be rare. Without going through the nitty gritty derivation, the Poisson distribution is given by:

$p(k)={\frac {\lambda ^{r}e^{-\lambda }}{r!}}$

The mean and variance are $\mu =\sigma ^{2}=\lambda$. In problems that need to use the Poisson distribution, the mean should be given.

Joint Distribution

Suppose we have a random variable $X$ with range $R_{X}=\{x_{1},x_{2},...,x_{i},...,x_{n}\}$ and with some probability mapping $p_{i}$. Say we also have another random variable $Y$ with range $R_{Y}=\{y_{1},y_{2},...,y_{i},...,y_{n}\}$ and with some probability mapping $q_{i}$. We define a joint probability distribution of $X$ and $Y$ by:

$p_{ij}=P((X\cap x_{i})\cap (Y\cap y_{j}))$

For $1\leq i\leq n$ and $1\leq j\leq m$.

Algebra of Random Variables

There are some useful algebra operations for random variables. Below is a short list and should be self explanatory:

1. $X+Y$ - Adding two random variables.
2. $X+\alpha$ - Adding a constant to a random variable.
3. $\alpha X$ - Multiplying some scalar to a random variable.
4. $XY$ - Multiplying two random variables together.

Some interesting properties for mean and variance include:

1. $E(X+Y)=E(X)+E(Y)$
2. $E(\alpha X)=\alpha E(X)$
3. ${\textrm {Var}}(\alpha X)=\alpha ^{2}{\textrm {Var}}(X)$

Exercises

Exercise 1

A fair die is thrown. Find the probability of (a) throwing a 6, (b) throwing an even number, (c) not throwing a 5, and (d) throwing a number less than 3 or more than 5.

Solution

Simply list all the possible outcomes of the values that a fair die can throw $\{1,2,3,4,5,6\}$.

(a) Suppose the event $A=\{6\}$. There is only 1 case out of the 6. Therefore the answer is $P(A)={\frac {1}{6}}$.

(b) Suppose event $B=\{2,4,6\}$. Therefore the answer is $P(B)={\frac {1}{2}}$.

(c) Suppose event $C=\{1,2,3,4,6\}$. Therefore the answer is $P(C)={\frac {5}{6}}$.

(d) Suppose event $D=\{1,2,6\}$. Therefore the answer is $P(D)={\frac {3}{6}}$.

Exercise 2

Suppose that, in a certain population, 40% of the people have red hair, 25% have tuberculosis, and 15% have both. What percentage has neither?

Solution

Let $P(R)=0.4$, $P(T)=0.25$, and $P(R\cap T)=0.15$. We are looking for $P({\overline {R\cup T}})$.

Since we know that $P(R\cup T)=P(R)+P(T)-P(R\cap T)$ then we can easily get $P(R\cup T)=0.5$. We also know that $P({\overline {R\cup T}})=1-P(R\cup T)$. Therefore the answer is $P({\overline {R\cup T}})=0.5$. Elementary right?

Exercise 3

An urn contains 5 red, 12 green, and 8 yellow balls. The three are drawn without replacement. (a) What is the probability that a red, a green, and a yellow ball will be drawn (in any order)? (b) What is the probability that the last ball to be drawn will be green?

Solution

(a) This problem is worthy of an extensive discussion. First, let's call the event $E$ to be the events that a red, green, and yellow will be drawn in any order. We would have $E=\{RGY,RYG,GRY,GYR,YRG,YGR\}$. Where $R$ is for red, $G$ is for green, and $Y$ is for yellow. Since we don't really care about the order, $P(RGY)$, $P(RYG)$, and all the rest are equivalent. Observe that:

$P(RGY)={\frac {5}{25}}\cdot {\frac {12}{24}}\cdot {\frac {8}{23}}={\frac {4}{115}}$

$P(RYG)={\frac {5}{25}}\cdot {\frac {8}{24}}\cdot {\frac {12}{23}}={\frac {4}{115}}$

All other combinations will still have the same probability. Therefore we only need to get one probability, say $P(RGY)$ and multiply it to the different combinations which is 6!

Hence the final answer would be $P(E)=6\cdot P(RGY)={\frac {24}{115}}$.

Sounds simple right? There's more to this. The $P(RGY)$ and all other combinations are actually the translation of $P(R\cap G\cap Y)$. Now let's dissect the $P(RGY)$ equation carefully. The first draw is $P(R)={\frac {5}{25}}$. The second draw is $P(G|R)={\frac {12}{24}}$. The third draw is $P(Y|G\cap R)={\frac {8}{23}}$. Explicitly we have $P(R\cap G\cap Y)=P(Y|G\cap R)P(G|R)P(R)$.

Doesn't this sound familiar? You're right! It follows the formula of $P(A\cap B\cap C)=P(C|B\cap A)P(B|A)P(A)$. Take note that $P(G\cap R)=P(G|R)P(R)$.

(b) This time we have a different set of outcomes. Let's set this as event $F=\{NNG,NGG,GNG,GGG\}$. While keeping the notion of conditional probability in mind. The final answer would be:

$P(F)={\frac {13}{25}}\cdot {\frac {12}{24}}\cdot {\frac {12}{23}}+{\frac {13}{25}}\cdot {\frac {12}{24}}\cdot {\frac {11}{23}}+{\frac {12}{25}}\cdot {\frac {13}{24}}\cdot {\frac {11}{23}}+{\frac {12}{25}}\cdot {\frac {11}{24}}\cdot {\frac {10}{23}}={\frac {12}{25}}$

Exercise 4

Consider the table below which describes the babies born in one week at a certain hospital. If a baby is chosen at random and turns out to be a boy, find the probability that it was born to a mother over the age of 30 years.

Number of babies born which are:	Born to mothers over 30 years old	Born to mothers less than 30 years old
Boys	34	49
Girls	41	44

Solution

This is a simple counting exercise. Let $A$ be the event a baby is born to a mother who is more than 30 years old. Let $B$ be the event that a baby is a boy. We have $|A\cap B|=34$ and $|B|=34+49=83$. Note that the $|\cdot |$ operation is the cardinality or magnitude which counts the number of items or elements. Therefore the final answer is $P(A|B)={\frac {34}{83}}$.

Another interpretation would be to get the probabilities $P(A\cap B)$ and $P(B)$ with respect to the entire space. Adding all numbers gives us $|S|=34+49+41+44=168$. Therefore $P(A\cap B)={\frac {34}{168}}$ and $P(B)={\frac {83}{168}}$. Trivially, $P(A|B)={\frac {P(A\cap B)}{P(B)}}={\frac {34}{83}}$.

Exercise 5

Figure 4: Probability distribution for the total number of heads of three successive coin tosses.

Three fair coins are tossed in succession. Find the probability distribution of the random variable $X$ indicating the total number of heads. Show a bar graph of this distribution. Find the mean, variance, and standard deviation.

Solution Easy! The list of possible outcomes would be $\{0,1,2,3\}$ and their probability mapping would be:

• $P(X=0)={\frac {1}{8}}$
• $P(X=1)={\frac {3}{8}}$
• $P(X=2)={\frac {3}{8}}$
• $P(X=3)={\frac {1}{8}}$

Figure 4 shows the bar graph for this problem. The mean, variance, and standard deviation are:

• $\mu =0\cdot {\frac {1}{8}}+1\cdot {\frac {3}{8}}+2\cdot {\frac {3}{8}}+3\cdot {\frac {1}{8}}=1.5$
• $\sigma ^{2}=(0-1.5)^{2}\cdot {\frac {1}{8}}+(1-1.5)^{2}\cdot {\frac {3}{8}}+(2-1.5)^{2}\cdot {\frac {3}{8}}+(3-1.5)^{2}\cdot {\frac {1}{8}}=0.75$
• $\sigma ={\sqrt {(}}0.75)\approx 0.866$

Exercise 6

Suppose an urn contains 7 red and 10 green balls, and 20 balls are drawn with replacement and mixing after each draw. What is the probability that (a) exactly 4, or (b) at least 4, of the balls are red?

Solution

First the probability of successfully drawing a red is $p={\frac {7}{17}}$. Probability of drawing NOT a red is $q=1-p={\frac {10}{17}}$. We can use the binomial probability distribution equation in here. Let $n=20$. Recall that:

$P(X=k)={n \choose k}p^{k}(1-p)^{n-k}$

(a) Here, $k=4$ and therefore the answer would be:

$P(X=4)={20 \choose 4}\left({\frac {7}{17}}\right)^{4}\left({\frac {10}{17}}\right)^{16}\approx 0.0286$

(b) Here, we need to add all probabilities from 4 to 20. Mathematically that would be:

$P(X\geq 4)=\sum _{k=4}^{20}{20 \choose k}\left({\frac {7}{17}}\right)^{k}\left({\frac {10}{17}}\right)^{20-k}$

However this is very tedious to do. Let's instead get $P(X\leq 3)$ (or $P(X<4)$) and compute $P(X\geq 4)=1-P(X\leq 3)$. We would have:

$P(X\geq 4)=1-P(X\leq 3)=1-\sum _{k=0}^{3}{20 \choose k}\left({\frac {7}{17}}\right)^{k}\left({\frac {10}{17}}\right)^{20-k}$

Expanding and plugging in values gives us:

$P(X\geq 4)=1-\left[{20 \choose 0}\left({\frac {7}{17}}\right)^{0}\left({\frac {10}{17}}\right)^{20}+{20 \choose 1}\left({\frac {7}{17}}\right)^{1}\left({\frac {10}{17}}\right)^{19}+{20 \choose 2}\left({\frac {7}{17}}\right)^{2}\left({\frac {10}{17}}\right)^{18}+{20 \choose 3}\left({\frac {7}{17}}\right)^{3}\left({\frac {10}{17}}\right)^{17}\right]\approx 0.9877$

References

• Applebaum, D. , Probability and Information: An Integrated Approach, Cambridge University Press, 2008.
• Hankerson, D.R., Harris, G.A., Johnson, P.D. , Introduction to Information Theory and Data Compression, CRC Press, 2003.