Chebyshev Filters

Chebyshev filters come in two flavors: the Type-I and Type-II.

The Chebyshev Type-I Low-Pass Filter

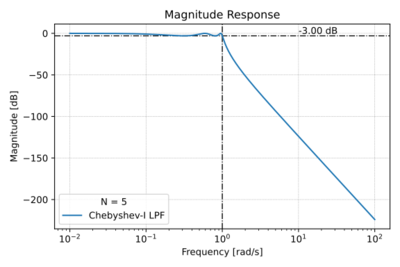
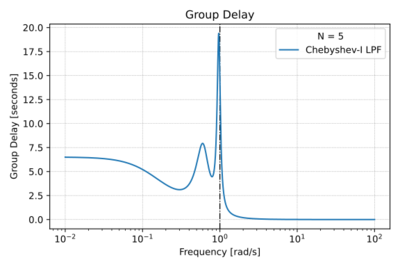
Chebyshev Type-I filters are also all-pole filters, with poles of the normalized ($\omega _{0}=1\,\mathrm {\tfrac {rad}{s}}$) filter located on an ellipse inside the unit circle, as shown in Fig. 1. This arrangement of poles results in (1) a shorter transition band, and therefore a steeper roll-off compared to the Butterworth low-pass filter of the same order, shown in Fig. 2, (2) poorer group delay characteristics as depicted in Figs. 3 and 4, and (3) ripples in the pass-band also seen in Fig. 2. By allowing larger ripples in the pass-band, we get: (1) a narrower transition band, and hence sharper cut-off, (2) higher Q poles, and (3) more degradation in the phase response.

Figure 1: The Chebyshev Type-I pole-zero with $N=5$ and a $3\,{\text{dB}}$ ripple.	Figure 2: The Chebyshev Type-I low-pass filter magnitude response with $N=5$ and a $3\,{\text{dB}}$ ripple.
Figure 3: The Chebyshev Type-I low-pass filter phase response with $N=5$ and a $3\,{\text{dB}}$ ripple.	Figure 4: The Chebyshev Type-I low-pass filter group delay with $N=5$ and a $3\,{\text{dB}}$ ripple.

The Chebyshev Type-I magnitude response is given by:

$\left|H\left(j\omega \right)\right|={\frac {1}{\sqrt {1+\varepsilon ^{2}\cdot T_{N}^{2}\left({\frac {\omega }{\omega _{0}}}\right)}}}$

(1)

Where $N$ is the filter order, $\omega _{0}$ is the cut-off frequency, $\varepsilon ={\sqrt {10^{\frac {\delta }{10}}-1}}$ is the ripple factor with ripple $\delta$ in dB, and $T_{N}\left(x\right)$ are solutions to the Chebyshev differential equation:

$\left(1-x^{2}\right){\frac {\partial ^{2}y}{\partial x^{2}}}-x{\frac {\partial y}{\partial x}}+N^{2}y=0$

(2)

For a normalized filter, or $\omega _{0}=1\,\mathrm {\tfrac {rad}{s}}$, the poles of the Chebyshev Type-I low-pass filter are the roots of $1+\varepsilon ^{2}\cdot T_{N}^{2}\left(-js\right)=0$. In practice, instead of solving this equation directly, we can easily get the roots (and hence the poles) of the filter transfer function using tools such as Python or Matlab.