Noise in RF Circuits

In this module, we consider the noise generated by the electronic devices themselves due to the (1) random motion of electrons due to thermal energy and (2) the discreteness of electric charge. We see this as thermal noise in resistances, and shot noise in PN junctions. In MOS transistors, we also see flicker noise. This noise is not fundamental, but is due to the way MOS transistors are manufactured, This added uncertainty in the voltages and currents limit the smallest signal amplitude or power that our circuits can detect and/or process, limiting the transmission range and power requirements for reliable communications.

Modeling Noise

Figure 1: Random movement of an electron in an electric field.

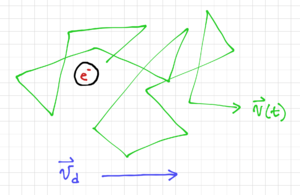
Since electronic noise is random, we cannot predict its value at any given time. However, we can describe noise in terms of its aggregate characteristics or statistics, such as its probability distribution function (pdf). As expected from the Central Limit Theorem, the pdf of the random movement of many electrons would approach a Gaussian distribution with zero mean since the electrons will move around instantaneously, but without any excitation, it will, on the average, stay in the same point in space. If we add an electric field, then the electron will move with an average drift velocity, ${\vec {v}}_{d}=-\mu _{e}{\vec {E}}$, but at any point in time, it would be moving with an instantaneous velocity ${\vec {v}}\left(t\right)\neq {\vec {v}}_{d}$, as shown in Fig. 1. Note that $\mu _{e}$ is the electron mobility.

Noise Power

Aside from the mean, to describe a zero-mean Gaussian random variable, $X$, we need the variance, $\sigma ^{2}=\left\langle X^{2}\right\rangle$, or the mean of $X^{2}$. For random voltages or currents, $n\left(t\right)$, this is equal to the average power over time, normalized to $1\,\mathrm {\Omega }$:

$P_{n}=\lim _{T\rightarrow \infty }{\frac {1}{T}}\int _{0}^{T}n^{2}\left(t\right)dt$

(1)

Figure 2: Zero-mean noise signals in time with different variances.

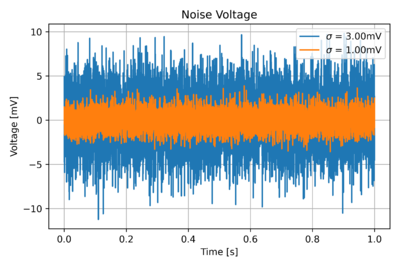
Thus, to describe noise, we can use its variance, or equivalently its average power. Fig. 2 illustrates the difference between two noise signals with different variances. Recall that $\sigma$, the square root of the variance, is the standard deviation.

Consider a noise voltage in time, $v_{n}\!\left(t\right)$, similar to the ones depicted in Fig. 2. The mean is then:

${\overline {v_{n}}}=\lim _{T\rightarrow \infty }{\frac {1}{T}}\int _{0}^{T}v_{n}\!\left(t\right)dt=0$

(2)

The variance, however, is non-zero:

${\overline {v_{n}^{2}}}=\lim _{T\rightarrow \infty }{\frac {1}{T}}\int _{0}^{T}v_{n}^{2}\!\left(t\right)dt\neq 0$

(3)

We can also calculate the root-mean-square or RMS as:

$v_{n,\mathrm {rms} }={\sqrt {\overline {v_{n}^{2}}}}={\sqrt {\lim _{T\rightarrow \infty }{\frac {1}{T}}\int _{0}^{T}v_{n}^{2}\!\left(t\right)dt}}$

(4)

Noise Power Spectrum

We can also examine the noise in the frequency domain, specifically, how noise power is distributed over frequency. Many noise sources are white, i.e. the noise power is distributed evenly across all frequencies, as seen in Fig. 3. Thus, white noise is totally unpredictable in time since there is no correlation between the noise at time $t_{1}$ and the noise at time time $t_{1}+\delta$, no matter how small $\delta$ is.