|
|
| Line 119: |
Line 119: |
| | The above relationships between mutual information and the entropies are illustrated in Fig. 2. Note that <math>H\left(A\mid A\right) = 0</math> since <math>P\left(a_i\mid a_i\right)=1</math>. We can then write: | | The above relationships between mutual information and the entropies are illustrated in Fig. 2. Note that <math>H\left(A\mid A\right) = 0</math> since <math>P\left(a_i\mid a_i\right)=1</math>. We can then write: |
| | | | |
| − | {{NumBlk|::|<math>I\left(A; A\right)=H\left(A\mid A\right) + H\left(A\right) =H\left(A\right) </math>|{{EquationRef|19}}}} | + | {{NumBlk|::|<math>I\left(A; A\right)=H\left(A\right) -H\left(A\mid A\right) =H\left(A\right) </math>|{{EquationRef|19}}}} |
| | | | |
| | Thus, we can think of entropy as ''self-information''. | | Thus, we can think of entropy as ''self-information''. |
In general, the channel itself can add noise. This means that the channel adds an additional layer of uncertainty to our transmissions. Consider a channel with input symbols  , and output symbols
, and output symbols  . Note that the input and output alphabets do not need to have the same number of symbols. Given the noise in the channel, if we observe the output symbol
. Note that the input and output alphabets do not need to have the same number of symbols. Given the noise in the channel, if we observe the output symbol  , we are not sure which
, we are not sure which  was the input symbol.
was the input symbol.
We can then characterize the discrete channel as a set of probabilities  . If the probability distribution of the outputs depend on the current input, then the channel is memoryless. Let us consider the information we get from observing a symbol
. If the probability distribution of the outputs depend on the current input, then the channel is memoryless. Let us consider the information we get from observing a symbol  at the output of a discrete memoryless channel (DMC).
at the output of a discrete memoryless channel (DMC).
Definition

Figure 1: A noisy channel.
Given a probability model of the source, we have an a priori estimate  that symbol
that symbol  will be sent next. Upon observing
will be sent next. Upon observing  , we can revise our estimate to
, we can revise our estimate to  , as shown in Fig. 1. The change in information, or mutual information, is given by:
, as shown in Fig. 1. The change in information, or mutual information, is given by:
-
 |
|
(1)
|
Let's look at a few properties of mutual information. Expressing the equation above in terms of  :
:
-
 |
|
(2)
|
Thus, we can say:
-
 |
|
(3)
|
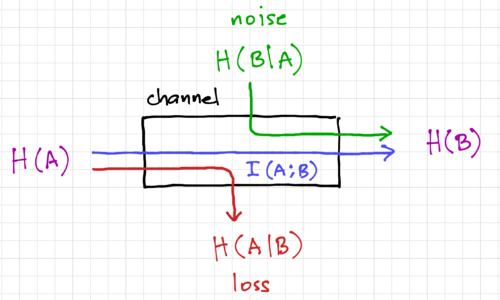
Figure 2: An information channel.
This is expected since, after observing  , the amount of uncertainty is reduced, i.e. we know a bit more about
, the amount of uncertainty is reduced, i.e. we know a bit more about  , and the most change in information we can get is when
, and the most change in information we can get is when  and
and  are perfectly correlated, with
are perfectly correlated, with  . Thus, we can think of mutual information as the average information conveyed across the channel, as shown in Fig. 2. From Bayes' Theorem, we have the property:
. Thus, we can think of mutual information as the average information conveyed across the channel, as shown in Fig. 2. From Bayes' Theorem, we have the property:
-
 |
|
(4)
|
Note that if  and
and  are independent, where
are independent, where  and
and  , then:
, then:
-
 |
|
(5)
|
We can get the average mutual information over all the input symbols as:
-
 |
|
(6)
|
Similarly, for all the output symbols:
-
 |
|
(7)
|
For both input and output symbols, we get:
-
 |
|
(8)
|
Non-Negativity of Mutual Information
To show the non-negativity of mutual information, let us use Jensen's Inequality, which states that for a convex function,  :
:
-
 |
|
(9)
|
Using the fact that  is convex, and applying this to our expression for mutual information, we get:
is convex, and applying this to our expression for mutual information, we get:
-
 |
|
(10)
|
Note that  when
when  and
and  are independent.
are independent.
Conditional and Joint Entropy
Given  and
and  , and their entropies:
, and their entropies:
-
 |
|
(11)
|
-
 |
|
(12)
|
Conditional Entropy
The conditional entropy is a measure of the average uncertainty about  when
when  is known, and we can define it as:
is known, and we can define it as:
-
 |
|
(13)
|
And similarly,
-
 |
|
(14)
|
Joint Entropy
If we extend the definition of entropy to two (or more) random variables,  and
and  , we can define the joint entropy of
, we can define the joint entropy of  and
and  as:
as:
-
 |
|
(15)
|
Expanding expression for joint entropy, and using  we get:
we get:
-
 |
|
(16)
|
If we instead used  , we would get the alternative expression:
, we would get the alternative expression:
-
 |
|
(17)
|
We can then expand our expression for  as:
as:
-
 |
|
(18)
|
The above relationships between mutual information and the entropies are illustrated in Fig. 2. Note that  since
since  . We can then write:
. We can then write:
-
 |
|
(19)
|
Thus, we can think of entropy as self-information.
Channel Capacity
The maximum amount of information that can be transmitted through a discrete memoryless channel, or the channel capacity, with units bits per channel use, can then be thought of as the maximum mutual information over all possible input probability distributions:
-
 |
|
(20)
|
Or equivalently, we need to choose  such that we maximize
such that we maximize  . Since:
. Since:
-
 |
|
(21)
|
And if we are using the channel at its capacity, then for every  :
:
-
 |
|
(22)
|
Thus, we can maximize channel use by maximizing the use for each symbol independently. From the definition of mutual information and from the Gibbs inequality, we can see that:
-
 |
|
(23)
|
Where  and
and  are the number of symbols in
are the number of symbols in  and
and  respectively. Thus, the channel capacity of a channel is limited by the logarithm of the number of distinguishable symbols at its input (or output).
respectively. Thus, the channel capacity of a channel is limited by the logarithm of the number of distinguishable symbols at its input (or output).
Sources
- Tom Carter's notes on Information Theory
- Dan Hirschberg's notes on Data Compression
- Lance Williams' notes on Geometric and Probabilistic Methods in Computer Science
References
















































