161-A2.1

• Activity: Source Coding
• Instructions: In this activity, you are tasked to
  • Walk through the examples.
  • Write a short program to compress and decompress a redundant file.
• Should you have any questions, clarifications, or issues, please contact your instructor as soon as possible.

Example 1: Uniquely Decodable Codes

Let us try to encode a source with just four symbols in its alphabet, i.e. $A=\{a_{1},a_{2},a_{3},a_{4}\}$, with probability distribution $P=\{0.5,0.25,0.125,0.125\}$. We can calculate the entropy of this source as:

$H\left(S\right)=0.5\log _{2}\left({\frac {1}{0.5}}\right)+0.25\log _{2}\left({\frac {1}{0.25}}\right)+0.125\log _{2}\left({\frac {1}{0.125}}\right)+0.125\log _{2}\left({\frac {1}{0.125}}\right)=1.75\,\mathrm {bits}$

(1)

Let us look at a few bit sequence assignments and see if they are uniquely decodable or not.

Symbol	Probability	Code 1	Code 2	Code 3	Code 4
$a_{1}$	0.5	0	0	0	0
$a_{2}$	0.25	0	1	10	01
$a_{3}$	0.125	1	00	110	011
$a_{4}$	0.125	10	11	111	0111
Average Code Length:		1.125	1.25	1.75	1.875

Recall that Shannon's Noiseless Coding Theorem states that $H\left(S\right)\leq L=1.75\,\mathrm {bits}$. Thus, codes 1 and 2 are not uniquely decodable since they have average code lengths less than $L$.

For code 1, since there are two symbols sharing an encoded symbol, we can say that it is not a distinct code, and therefore not uniquely decodable. We can check code 2 by taking a sequence of symbols encoded using this code: $0011$. We can easily see that this message can be decoded in different ways, either as $0,0,1,1$, or $00,11$.

Code 3 has one of the most desirable properties of a code: having its average length equal to the entropy of the source, and according to Shannon, you cannot have a uniquely decodable code with an average length shorter than this. We can also see that for a sequence of symbols encoded using code 3, there is only one way you can decode the message, thus it is uniquely decodable.

Code 4 is also uniquely decodable, however, it is not instantaneous, since the decoder needs to see the start of the next symbol to determine the end of the current symbol. Also note that the average length of code 4 is longer than the $H\left(S\right)$.

We can use the Kraft-McMillan Inequality, $K=\sum _{i=1}^{n}{\tfrac {1}{r^{\ell _{i}}}}\leq 1$, to test if a code is uniquely decodable. Tabulating the values, we get:

Code	$K$
1	1.75
2	1.5
3	1.0
4	0.9375

As expected, codes 1 and 2 have $K>1$, and thus, are not uniquely decodable, while codes 3 and 4 have $K\leq 1$, and hence, they are uniquely decodable.

Example 2: Uniformly Distributed Symbols

Let us consider the case when the symbols are uniformly distributed, i.e. $P=\{0.25,0.25,0.25,0.25\}$. We can then calculate the entropy of the source as:

$H\left(S\right)=0.25\log _{2}\left({\frac {1}{0.25}}\right)+0.25\log _{2}\left({\frac {1}{0.25}}\right)+0.25\log _{2}\left({\frac {1}{0.25}}\right)+0.25\log _{2}\left({\frac {1}{0.25}}\right)=2\,\mathrm {bits}$

(2)

In this case, the source is incompressible. Thus, we can just use a fixed length code $00,01,10,11$.

Example 3: Prefix Codes

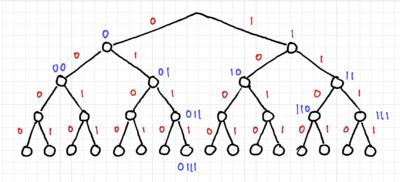
In prefix codes or prefix-free codes, no codeword is a proper prefix of another. One way to test this is to use trees. Fig. 1 shows a binary tree with 4 levels. This three can represent codewords with lengths of 1 to 4 bits. Thus, for a prefix code, all the codewords should only be at the leaves of the tree, or equivalently, at nodes without any codewords further down the tree.

Fig. 1: A 4-level binary tree.

Fig. 2: A binary tree for code 2.

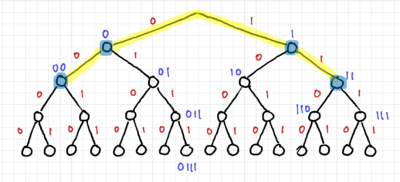
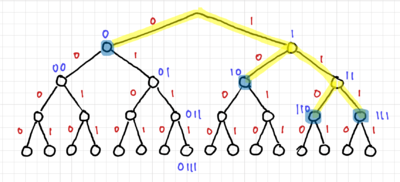
The tree for code 2 is shown in Fig. 2, and we can easily see that code 2 is not a prefix code since there are codewords within the tree. Fig. 3 shows the tree for code 3, and since all the codewords are at the edges of the tree, it is a prefix code, and thus uniquely decodable and instantaneous. Lastly, we have the tree for code 4 in Fig. 4, where only one of the codewords is at the edge of the tree. Thus, code 4 is not a prefix code.

Fig. 3: A binary tree for code 3.

Fig. 4: A binary tree for code 4.

Example 4: Huffman Coding

Huffman codes are an optimal variable-length prefix code, commonly used for lossless data compression. The algorithm for generating these codes was developed by David Huffman, and was published in his 1952 paper when he was a graduate student at MIT. Similar to all our entropy-based codes, shorter codes are assigned to symbols with higher probabilities.

Coding the Source

Given a source with alphabet $A=\{a_{1},a_{2},a_{3},a_{4},a_{5}\}$, with probabilities $P=\{0.15,0.2,0.25,0.25,0.15\}$, generate a Huffman code for this source.

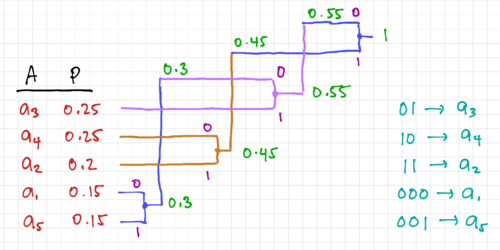
The first step is to sort the symbols according to their probabilities, as shown in Fig. 5. We then choose the two symbols with the lowest probabilities ($a_{1}$) and ($a_{5}$), and combine them into a new symbol, whose probability is $0.15+0.15=0.3$. The symbols are then sorted once again. We repeat this process until we combine all the symbols into one symbol with probability equal to 1.

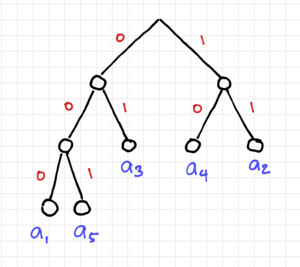
Working backwards from the root of our tree, we can assign a '0' to the top fork, and a '1' to the bottom fork until we get to the original symbols. Fig. 6 shows the redrawn Huffman tree showing the codewords at the endpoints of the tree.

Figure 5: Huffman coding a source.

Figure 6: The resulting Huffman tree.

This process results in the following codes:

Symbol	Code
$a_{1}$	000
$a_{2}$	11
$a_{3}$	01
$a_{4}$	10
$a_{5}$	001

Evaluating the Code

Let us check how good our Huffman code is. First, let us compute the entropy of the source:

$H\left(S\right)=0.15\log _{2}\left({\frac {1}{0.15}}\right)+0.2\log _{2}\left({\frac {1}{0.2}}\right)+0.25\log _{2}\left({\frac {1}{0.25}}\right)+0.25\log _{2}\left({\frac {1}{0.25}}\right)+0.15\log _{2}\left({\frac {1}{0.15}}\right)=2.285\,\mathrm {bits}$

(2)

The average code length of our Huffman code is:

$L=0.15\cdot 3+0.2\cdot 2+0.25\cdot 2+0.25\cdot 2+0.15\cdot 3=2.3\,\mathrm {bits}$

(3)

We can see that our Huffman code is very efficient, with the average length very close to the Shannon limit.