Difference between revisions of "Shannon's Communication Theory"
| Line 7: | Line 7: | ||
Note that sending information in space, e.g. from ''here'' to ''there'' is equivalent sending information in time, e.g. from ''now'' to ''then''. Thus, Shannon's theory applies to both information transmission and information storage. | Note that sending information in space, e.g. from ''here'' to ''there'' is equivalent sending information in time, e.g. from ''now'' to ''then''. Thus, Shannon's theory applies to both information transmission and information storage. | ||
| + | |||
| + | === Shannon's Noiseless Coding Theorem === | ||
| + | One very important question to ask is: "How efficiently can we encode the information that we want to send through the channel?" | ||
== Shannon's Theory for Analog Channels == | == Shannon's Theory for Analog Channels == | ||
Revision as of 16:17, 14 September 2020
Contents
A First Look at Shannon's Communication Theory
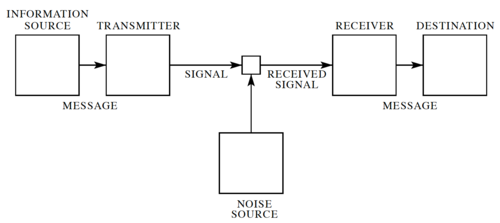
In his landmark 1948 paper[1], Claude Shannon developed a general model for communication systems, as well as a framework for analyzing these systems. The model has three components: (1) the sender or source, (2) the channel, and (3) the receiver or sink. The model also includes the transmitter that encodes the message into a signal, the receiver, for decoding the signal back into a message, as well the noise of the channel, as shown in Fig. 1.
In Shannon's discrete model, the source provides a stream of symbols from a finite alphabet, , which are then encoded. The code is sent through the channel, which could be corrupted by noise, and when the code reaches the other end, it is decoded by the receiver, and then the sink extracts information from the steam of symbols.
Note that sending information in space, e.g. from here to there is equivalent sending information in time, e.g. from now to then. Thus, Shannon's theory applies to both information transmission and information storage.
Shannon's Noiseless Coding Theorem
One very important question to ask is: "How efficiently can we encode the information that we want to send through the channel?"
