Difference between revisions of "161-A3.1"
| (36 intermediate revisions by the same user not shown) | |||
| Line 6: | Line 6: | ||
== Example 1: Mutual Information == | == Example 1: Mutual Information == | ||
| − | Given the following probabilities: | + | Given the following joint probabilities: |
{| class="wikitable" style="text-align: center; width: 45%;" | {| class="wikitable" style="text-align: center; width: 45%;" | ||
| Line 81: | Line 81: | ||
== Example 2: A Noiseless Binary Channel == | == Example 2: A Noiseless Binary Channel == | ||
| + | [[File:Noiseless binary channel.png|thumb|350px|Figure 1: Channel model for a noiseless binary channel.]] | ||
Consider transmitting information over a noiseless binary channel shown in Fig. 1. The input, <math>A=\{0, 1\}</math> has ''a priori'' probabilities <math>P\left(A=0\right)=\alpha</math> and <math>P\left(A=1\right)=1-\alpha</math>, and the output is <math>B=\{0,1\}</math>. Calculating the output probabilities: | Consider transmitting information over a noiseless binary channel shown in Fig. 1. The input, <math>A=\{0, 1\}</math> has ''a priori'' probabilities <math>P\left(A=0\right)=\alpha</math> and <math>P\left(A=1\right)=1-\alpha</math>, and the output is <math>B=\{0,1\}</math>. Calculating the output probabilities: | ||
| Line 103: | Line 104: | ||
The conditional entropy, <math>H\left(B\mid A\right)</math> is then: | The conditional entropy, <math>H\left(B\mid A\right)</math> is then: | ||
| − | {{NumBlk|::|<math>\begin{align} H\left(B\mid A\right) = & \sum_{i=1}^n P\left(a_i\right) \sum_{j=1}^m P\left(b_j\mid a_i\right)\cdot\log_2\left(\frac{1}{P\left(b_j\mid a_i\right)}\right)\\ | + | {{NumBlk|::|<math>\begin{align} H\left(B\mid A\right) = &\,\, \sum_{i=1}^n P\left(a_i\right) \sum_{j=1}^m P\left(b_j\mid a_i\right)\cdot\log_2\left(\frac{1}{P\left(b_j\mid a_i\right)}\right)\\ |
| − | = & P\left(A=0\right)\cdot P\left(B=0\mid A=0\right)\cdot \log_2\frac{1}{P\left(B=0\mid A=0\right)} \\ | + | = &\,\, P\left(A=0\right)\cdot P\left(B=0\mid A=0\right)\cdot \log_2\frac{1}{P\left(B=0\mid A=0\right)} \\ |
| − | & + | + | & + P\left(A=0\right)\cdot P\left(B=1\mid A=0\right)\cdot \log_2\frac{1}{P\left(B=1\mid A=0\right)} \\ |
| + | & + P\left(A=1\right)\cdot P\left(B=0\mid A=1\right)\cdot \log_2\frac{1}{P\left(B=0\mid A=1\right)} \\ | ||
| + | & + P\left(A=1\right)\cdot P\left(B=1\mid A=1\right)\cdot \log_2\frac{1}{P\left(B=1\mid A=1\right)} \\ | ||
| + | = &\,\, \alpha \cdot 1\cdot \log_2 1 \\ | ||
| + | & + \alpha\cdot 0\cdot \log_2\frac{1}{0} \\ | ||
| + | & + \left(1-\alpha\right)\cdot 0\cdot \log_2\frac{1}{0} \\ | ||
| + | & + \left(1-\alpha\right)\cdot 1\cdot \log_2 1 \\ | ||
| + | = &\,\, 0 \\ | ||
\end{align}</math>|{{EquationRef|13}}}} | \end{align}</math>|{{EquationRef|13}}}} | ||
| + | |||
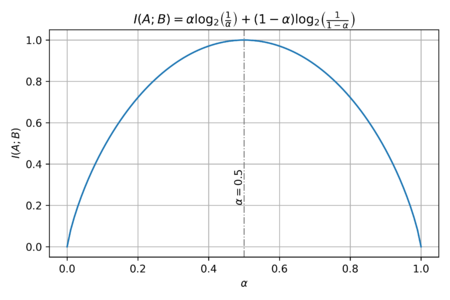
| + | [[File:Bernoulli H.png|thumb|450px|Figure 2: The mutual information as a function of <math>\alpha</math>.]] | ||
| + | Which is expected since <math>A</math> and <math>B</math> are perfectly correlated, and there is no uncertainty in <math>B</math> once <math>A</math> is given. Thus, the mutual information is: | ||
| + | |||
| + | {{NumBlk|::|<math>\begin{align} | ||
| + | I\left(A;B\right) & =H\left(B\right)-H\left(B\mid A\right) = H\left(B\right) \\ | ||
| + | & = \alpha\log_2\frac{1}{\alpha} + \left(1-\alpha\right)\log_2\frac{1}{1-\alpha} \\ | ||
| + | \end{align}</math>|{{EquationRef|14}}}} | ||
| + | |||
| + | The plot of the mutual information as a function of <math>\alpha</math> is shown in Fig. 2. To get the channel capacity, we get the maximum <math>I\left(A;B\right)</math> over all <math>\alpha</math>. Thus, we can take the derivative of the mutual information and set it equal to zero, to find the optimal <math>\alpha</math>. And noting that <math>\log_2 x = \tfrac{1}{\ln 2}\ln x</math>, we get: | ||
| + | |||
| + | {{NumBlk|::|<math>\begin{align} | ||
| + | \frac{\partial I\left(A;B\right)}{\partial \alpha} & = \frac{\partial}{\partial \alpha}\left( \alpha\log_2\frac{1}{\alpha} + \left(1-\alpha\right)\log_2\frac{1}{1-\alpha} \right) = 0\\ | ||
| + | & = \frac{\partial}{\partial \alpha}\left(\frac{\alpha}{\ln 2}\ln\frac{1}{\alpha} + \frac{1-\alpha}{\ln 2}\ln\frac{1}{1-\alpha}\right) = 0\\ | ||
| + | & = \frac{1}{\ln 2}\ln\frac{1}{\alpha} - \alpha\frac{1}{\alpha^2}\frac{\alpha}{\ln 2} - \frac{1}{\ln 2}\ln \frac{1}{1-\alpha} + \frac{1-\alpha}{\ln 2}\frac{1-\alpha}{\left(1-\alpha\right)^2} = 0\\ | ||
| + | & = \ln\frac{1}{\alpha} - \ln\frac{1}{1-\alpha} = 0\\ | ||
| + | \end{align}</math>|{{EquationRef|15}}}} | ||
| + | |||
| + | Thus, we can get <math>\alpha = 0.5</math>, as expected from Fig. 2. Therefore the channel capacity is: | ||
| + | |||
| + | {{NumBlk|::|<math>C = \max_{P\left(A\right)} I\left(A;B\right)= \left. I\left(A;B\right)\right|_{\alpha = 0.5} = 1\,\mathrm{bit/channel\,use}</math>|{{EquationRef|16}}}} | ||
| + | |||
| + | As expected, in a noiseless binary channel, we can transmit a maximum of 1 bit of information per channel use. | ||
== Example 3: A Noisy Channel with Non-Overlapping Outputs == | == Example 3: A Noisy Channel with Non-Overlapping Outputs == | ||
| + | [[File:Nonoverlaping channel.png|thumb|350px|Figure 3: A noisy channel with non-overlapping outputs.]] | ||
| + | Consider the channel shown in Fig. 3. The input, <math>A=\{0, 1\}</math> has ''a priori'' probabilities <math>P\left(A=0\right)=\alpha</math> and <math>P\left(A=1\right)=1-\alpha</math>, and in this case, the output is <math>B=\{1, 2, 3, 4\}</math>. Once again, we can calculate the output probabilities: | ||
| + | |||
| + | {{NumBlk|::|<math>P\left(B=1\right) = P\left(B=1\mid A=0\right)\cdot P\left(A=0\right) = \frac{1}{2}\cdot \alpha</math>|{{EquationRef|17}}}} | ||
| + | {{NumBlk|::|<math>P\left(B=2\right) = P\left(B=2\mid A=0\right)\cdot P\left(A=0\right) = \frac{1}{2}\cdot \alpha</math>|{{EquationRef|18}}}} | ||
| + | {{NumBlk|::|<math>P\left(B=3\right) = P\left(B=3\mid A=1\right)\cdot P\left(A=1\right) = \frac{1}{3}\cdot \left(1-\alpha\right)</math>|{{EquationRef|19}}}} | ||
| + | {{NumBlk|::|<math>P\left(B=4\right) = P\left(B=4\mid A=1\right)\cdot P\left(A=1\right) = \frac{2}{3}\cdot \left(1-\alpha\right)</math>|{{EquationRef|20}}}} | ||
| + | |||
| + | Note that the terms that evaluate to zero have already been omitted. The entropy at the output is then: | ||
| + | |||
| + | {{NumBlk|::|<math>\begin{align} | ||
| + | H\left(B\right) & = \frac{\alpha}{2}\log_2\frac{2}{\alpha} + \frac{\alpha}{2}\log_2\frac{2}{\alpha} + \frac{1-\alpha}{3}\log_2\frac{3}{1-\alpha} +\frac{2\left(1-\alpha\right)}{3}\log_2\frac{3}{2\left(1-\alpha\right)} \\ | ||
| + | & = \alpha \log_2\frac{1}{\alpha} + \left(1-\alpha\right)\log_2\frac{1}{1-\alpha} + \alpha\log_2 2 + \left(1-\alpha\right)\left(\log_2 3 - \frac{2}{3}\log_2 2\right)\\ | ||
| + | \end{align}</math>|{{EquationRef|21}}}} | ||
| + | |||
| + | Calculating the conditional entropy: | ||
| + | |||
| + | {{NumBlk|::|<math>\begin{align} | ||
| + | H\left(B\mid A\right) = &\,\, P\left(A=0\right) P\left(B=1\mid A=0\right)\cdot \log_2\frac{1}{P\left(B=1\mid A=0\right)} \\ | ||
| + | &\,\, + P\left(A=0\right) P\left(B=2\mid A=0\right)\cdot \log_2\frac{1}{P\left(B=2\mid A=0\right)} \\ | ||
| + | &\,\, + P\left(A=1\right) P\left(B=3\mid A=1\right)\cdot \log_2\frac{1}{P\left(B=3\mid A=1\right)} \\ | ||
| + | &\,\, + P\left(A=1\right) P\left(B=4\mid A=1\right)\cdot \log_2\frac{1}{P\left(B=4\mid A=1\right)} \\ | ||
| + | = &\,\, \frac{\alpha}{2}\cdot \log_2 2 + \frac{\alpha}{2}\cdot \log_2 2 + \frac{1-\alpha}{3}\cdot \log_2 3 + \frac{2\left(1-\alpha\right)}{3}\cdot \log_2 \frac{3}{2} \\ | ||
| + | = & \,\, \alpha \cdot \log_2 2 + \left(1-\alpha\right)\left(\log_2 3 - \frac{2}{3}\log_2 2\right) \\ | ||
| + | \end{align}</math>|{{EquationRef|22}}}} | ||
| + | |||
| + | This allows us to calculate the mutual information: | ||
| + | |||
| + | {{NumBlk|::|<math>\begin{align} | ||
| + | I\left(A;B\right) & =H\left(B\right)-H\left(B\mid A\right) \\ | ||
| + | & = \alpha\log_2\frac{1}{\alpha} + \left(1-\alpha\right)\log_2\frac{1}{1-\alpha} \\ | ||
| + | \end{align}</math>|{{EquationRef|23}}}} | ||
| + | |||
| + | Which once again leads to a channel capacity, <math>C=1</math> bit per channel use, at <math>\alpha=0.5</math>. This reinforces our intuition that as long as each output symbol is determined by only one input symbol, i.e. no overlaps, we can infer which input symbol was transmitted when we know the output symbol even in the presence of noise. | ||
| + | |||
| + | == Activity: The Binary Symmetric Channel (BSC) == | ||
| + | [[File:Bsc.png|thumb|350px|Figure 4: The binary symmetric channel.]] | ||
| + | A more realistic channel model is the Binary Symmetric Channel shown in Fig. 4. For this channel, there is a probability <math>p</math> that if a '''0''' is transmitted, the channel corrupts it into a '''1'''. The same is true for transmitting a '''1''', there is a probability <math>p</math> that the output is converted to a '''0'''. | ||
| + | Given the input, <math>A=\{0, 1\}</math> has ''a priori'' probabilities <math>P\left(A=0\right)=\alpha</math> and <math>P\left(A=1\right)=1-\alpha</math>, calculate the following in terms of <math>\alpha</math> and <math>p</math>: | ||
| + | # The output probabilities <math>P\left(B=0\right)</math> and <math>P\left(B=1\right)</math>. | ||
| + | # The entropy at the output, <math>H\left(B\right)</math>. | ||
| + | # The conditional entropy, <math>H\left(B\mid A\right)</math>. | ||
| + | # The mutual information, <math>I\left(A;B\right)</math>. | ||
| + | # The channel capacity, <math>C</math> and show that <math>C=1-H\left(p\right)</math> where <math>H\left(p\right)=p\log_2 \tfrac {1}{p} + \left(1-p\right)\log_2 \tfrac{1}{1-p}</math>. | ||
| − | == | + | === Report Guide === |
| + | In addition to your calculations, include a short explanation of your procedure in obtaining the channel capacity from the your expression for mutual information. Also, comment on the behavior of the channel capacity as <math>p</math> is varied. Is this the behavior you expect? Send your reports via email before you start Module 4. | ||
== Sources == | == Sources == | ||
* Yao Xie's [https://www2.isye.gatech.edu/~yxie77/ece587/Lecture2.pdf slides] on Entropy and Mutual Information | * Yao Xie's [https://www2.isye.gatech.edu/~yxie77/ece587/Lecture2.pdf slides] on Entropy and Mutual Information | ||
Latest revision as of 10:24, 3 October 2020
- Activity: Mutual Information and Channel Capacity
- Instructions: In this activity, you are tasked to
- Walk through the examples.
- Calculate the channel capacity of different channel models.
- Should you have any questions, clarifications, or issues, please contact your instructor as soon as possible.
Contents
Example 1: Mutual Information
Given the following joint probabilities:
| A | B | AB | O | |
|---|---|---|---|---|
| Very Low | 1/8 | 1/16 | 1/32 | 1/32 |
| Low | 1/16 | 1/8 | 1/32 | 1/32 |
| Medium | 1/16 | 1/16 | 1/16 | 1/16 |
| High | 1/4 | 0 | 0 | 0 |
To get the entropies of and , we need to calculate the marginal probabilities:
-
(1)
-
-
(2)
-
And since:
-
(3)
-
We get:
-
(4)
-
-
(5)
-
Calculating the conditional entropies using:
-
(6)
-
-
(7)
-
Note that . Calculating the mutual information, we get:
-
(8)
-
Or equivalently:
-
(9)
-
Let us try to understand what this means:
- If we only consider , we have the a priori probabilities, for each blood type, and we can calculate the entropy, , i.e. the expected value of the information we get when we observe the results of the blood test.
- Will our expectations change if we do not have access to the blood test, but instead, we get to access (1) the person's susceptibility to skin cancer, and (2) the joint probabilities in Table 1? Since we are given more information, we expect one of the following:
- The uncertainty to be equal to the original uncertainty if and are independent, since , thus .
- A reduction in the uncertainty equal to , due to the additional information given by .
- If and are perfectly correlated, we reduce the uncertainty to zero since and .
Example 2: A Noiseless Binary Channel
Consider transmitting information over a noiseless binary channel shown in Fig. 1. The input, has a priori probabilities and , and the output is . Calculating the output probabilities:
-
(10)
-
-
(11)
-
Thus, the entropy at the output is:
-
(12)
-
The conditional entropy, is then:
-
(13)
-
Which is expected since and are perfectly correlated, and there is no uncertainty in once is given. Thus, the mutual information is:
-
(14)
-
The plot of the mutual information as a function of is shown in Fig. 2. To get the channel capacity, we get the maximum over all . Thus, we can take the derivative of the mutual information and set it equal to zero, to find the optimal . And noting that , we get:
-
(15)
-
Thus, we can get , as expected from Fig. 2. Therefore the channel capacity is:
-
(16)
-
As expected, in a noiseless binary channel, we can transmit a maximum of 1 bit of information per channel use.
Example 3: A Noisy Channel with Non-Overlapping Outputs
Consider the channel shown in Fig. 3. The input, has a priori probabilities and , and in this case, the output is . Once again, we can calculate the output probabilities:
-
(17)
-
-
(18)
-
-
(19)
-
-
(20)
-
Note that the terms that evaluate to zero have already been omitted. The entropy at the output is then:
-
(21)
-
Calculating the conditional entropy:
-
(22)
-
This allows us to calculate the mutual information:
-
(23)
-
Which once again leads to a channel capacity, bit per channel use, at . This reinforces our intuition that as long as each output symbol is determined by only one input symbol, i.e. no overlaps, we can infer which input symbol was transmitted when we know the output symbol even in the presence of noise.
Activity: The Binary Symmetric Channel (BSC)
A more realistic channel model is the Binary Symmetric Channel shown in Fig. 4. For this channel, there is a probability that if a 0 is transmitted, the channel corrupts it into a 1. The same is true for transmitting a 1, there is a probability that the output is converted to a 0.
Given the input, has a priori probabilities and , calculate the following in terms of and :
- The output probabilities and .
- The entropy at the output, .
- The conditional entropy, .
- The mutual information, .
- The channel capacity, and show that where .
Report Guide
In addition to your calculations, include a short explanation of your procedure in obtaining the channel capacity from the your expression for mutual information. Also, comment on the behavior of the channel capacity as is varied. Is this the behavior you expect? Send your reports via email before you start Module 4.
Sources
- Yao Xie's slides on Entropy and Mutual Information