Difference between revisions of "Resonance"
| (9 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | Resonance can be used to create zero impedance or zero admittance circuits at a particular resonant frequency, by either series or parallel connections of inductors and capacitors. However, care must be made not to exceed the maximum voltage or current ratings of the devices, especially in low-loss or high-<math>Q</math> circuits. | ||
| + | |||
== Series Resonant Circuits == | == Series Resonant Circuits == | ||
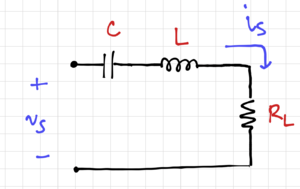
[[File:Series RLC.png|thumb|300px|Figure 1: A series RLC circuit.]] | [[File:Series RLC.png|thumb|300px|Figure 1: A series RLC circuit.]] | ||
| Line 10: | Line 12: | ||
{{NumBlk|::|<math>Z = R_L + j\left(\omega L - \frac{1}{\omega C}\right)</math>|{{EquationRef|2}}}} | {{NumBlk|::|<math>Z = R_L + j\left(\omega L - \frac{1}{\omega C}\right)</math>|{{EquationRef|2}}}} | ||
| + | === Resonant Frequency === | ||
We can see that the imaginary component of the impedance becomes zero at the '''resonant frequency''', <math>\omega_0</math>, equal to: | We can see that the imaginary component of the impedance becomes zero at the '''resonant frequency''', <math>\omega_0</math>, equal to: | ||
{{NumBlk|::|<math>\omega_0 = \frac{1}{\sqrt{L C}}</math>|{{EquationRef|3}}}} | {{NumBlk|::|<math>\omega_0 = \frac{1}{\sqrt{L C}}</math>|{{EquationRef|3}}}} | ||
| − | Note that the cancellation is ''narrowband'', since perfect cancellation occurs only at a single frequency. Thus, from the point of view of the voltage source <math>v_S</math>, the impedance <math>Z</math> is purely real. We can then calculate the current, <math>i_S</math> as: | + | Note that the cancellation is ''narrowband'', since perfect cancellation occurs only at a single frequency. Thus, from the point of view of the voltage source <math>v_S</math>, the impedance <math>Z</math> is purely real, and is equal to <math>R_L</math>. We can then calculate the current, <math>i_S</math> as: |
| − | {{NumBlk|::|<math>i_S = \frac{v_S}{R_L}</math>|{{EquationRef|4}}}} | + | {{NumBlk|::|<math>\left. i_S\right|_{\omega=\omega_0} =\left. \frac{v_S}{Z}\right|_{\omega=\omega_0}= \frac{v_S}{R_L}</math>|{{EquationRef|4}}}} |
We then use this current to calculate the voltage across the inductor and capacitor: | We then use this current to calculate the voltage across the inductor and capacitor: | ||
| − | {{NumBlk|::|<math>v_L = i_S \cdot j\omega_0 L = \frac{v_S}{R_L} \cdot j\omega_0 L = v_S \cdot jQ_S</math>|{{EquationRef|5}}}} | + | {{NumBlk|::|<math>\left. v_L\right|_{\omega=\omega_0} = i_S \cdot j\omega_0 L = \frac{v_S}{R_L} \cdot j\omega_0 L = v_S \cdot jQ_S</math>|{{EquationRef|5}}}} |
| − | {{NumBlk|::|<math>v_C = i_S \cdot \frac{1}{j\omega_0 C} = -\frac{v_S}{R_L} \cdot j\frac{1}{\omega_0 C} = -v_S \cdot jQ_S</math>|{{EquationRef|6}}}} | + | {{NumBlk|::|<math>\left. v_C\right|_{\omega=\omega_0} = i_S \cdot \frac{1}{j\omega_0 C} = -\frac{v_S}{R_L} \cdot j\frac{1}{\omega_0 C} = -v_S \cdot jQ_S</math>|{{EquationRef|6}}}} |
Where <math>Q_S</math> is the series circuit quality factor: | Where <math>Q_S</math> is the series circuit quality factor: | ||
| Line 35: | Line 38: | ||
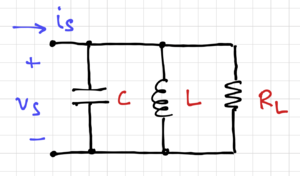
[[File:Parallel RLC.png|thumb|300px|Figure 2: A parallel RLC circuit.]] | [[File:Parallel RLC.png|thumb|300px|Figure 2: A parallel RLC circuit.]] | ||
| − | For the parallel resonant RLC circuit in Fig. 2, the total admittance seen by the current source is: | + | For the parallel resonant RLC circuit in Fig. 2, the total admittance seen by the current source, <math>i_S</math>, is: |
| − | {{NumBlk|::|<math>Y = \frac{1}{R_L} + j\omega C + \frac{1}{j\omega L} = \frac{1}{R_L} + j\left(\omega C - \frac{1}{\omega L}\right)</math>|{{EquationRef|8}}}} | + | {{NumBlk|::|<math>Y = \frac{1}{R_L} + j\omega C + \frac{1}{j\omega L} = \frac{1}{R_L} + j\left(\omega C - \frac{1}{\omega L}\right)=\frac{1}{Z}</math>|{{EquationRef|8}}}} |
The admittance becomes purely real at the resonant frequency, <math>\omega_0 = \tfrac{1}{\sqrt{LC}}</math>. Once again, we can calculate the voltage across <math>R_L</math> as: | The admittance becomes purely real at the resonant frequency, <math>\omega_0 = \tfrac{1}{\sqrt{LC}}</math>. Once again, we can calculate the voltage across <math>R_L</math> as: | ||
| − | {{NumBlk|::|<math>v_S = i_S \cdot R_L</math>|{{EquationRef|9}}}} | + | {{NumBlk|::|<math>\left. v_S\right|_{\omega=\omega_0} =\left. i_S \cdot Z\right|_{\omega=\omega_0} =i_S \cdot R_L</math>|{{EquationRef|9}}}} |
Thus, the currents through the inductor and capacitor can be expressed as: | Thus, the currents through the inductor and capacitor can be expressed as: | ||
| − | {{NumBlk|::|<math>i_L = \frac{v_S}{j\omega_0 L} = - i_S \cdot j\frac{R_L}{\omega_0 L} = -i_S \cdot jQ_P</math>|{{EquationRef|10}}}} | + | {{NumBlk|::|<math>\left. i_L\right|_{\omega=\omega_0} = \frac{v_S}{j\omega_0 L} = - i_S \cdot j\frac{R_L}{\omega_0 L} = -i_S \cdot jQ_P</math>|{{EquationRef|10}}}} |
| − | {{NumBlk|::|<math>i_C = v_S \cdot j\omega_0 C = i_S \cdot j\omega_0 R_L C = i_S \cdot jQ_P</math>|{{EquationRef|11}}}} | + | {{NumBlk|::|<math>\left. i_C\right|_{\omega=\omega_0} = v_S \cdot j\omega_0 C = i_S \cdot j\omega_0 R_L C = i_S \cdot jQ_P</math>|{{EquationRef|11}}}} |
Where the parallel quality factor, <math>Q_P</math> is equal to: | Where the parallel quality factor, <math>Q_P</math> is equal to: | ||
| Line 53: | Line 56: | ||
{{NumBlk|::|<math>Q_P = \frac{R_L}{\omega_0 L} = \omega_0 R_L C</math>|{{EquationRef|12}}}} | {{NumBlk|::|<math>Q_P = \frac{R_L}{\omega_0 L} = \omega_0 R_L C</math>|{{EquationRef|12}}}} | ||
| − | Similar to the series resonant circuit, we see that even though the currents | + | Similar to the series resonant circuit, we see that even though the currents through the reactances cancel out, the individual currents could be very large. |
Latest revision as of 14:46, 11 September 2020
Resonance can be used to create zero impedance or zero admittance circuits at a particular resonant frequency, by either series or parallel connections of inductors and capacitors. However, care must be made not to exceed the maximum voltage or current ratings of the devices, especially in low-loss or high- circuits.
Series Resonant Circuits
Consider the series resonant RLC circuit shown in Fig. 1. We can calculate the total impedance seen by the source , as:
-
(1)
-
Combining the imaginary terms of the impedance, we get:
-
(2)
-
Resonant Frequency
We can see that the imaginary component of the impedance becomes zero at the resonant frequency, , equal to:
-
(3)
-
Note that the cancellation is narrowband, since perfect cancellation occurs only at a single frequency. Thus, from the point of view of the voltage source , the impedance is purely real, and is equal to . We can then calculate the current, as:
-
(4)
-
We then use this current to calculate the voltage across the inductor and capacitor:
-
(5)
-
-
(6)
-
Where is the series circuit quality factor:
-
(7)
-
Note that:
- For small values of results in large values of , leading to large voltages across the inductor and capacitor.
- The voltage across the inductor is exactly out of phase with the capacitor voltage, thus cancelling each other out.
Parallel Resonant Circuits
For the parallel resonant RLC circuit in Fig. 2, the total admittance seen by the current source, , is:
-
(8)
-
The admittance becomes purely real at the resonant frequency, . Once again, we can calculate the voltage across as:
-
(9)
-
Thus, the currents through the inductor and capacitor can be expressed as:
-
(10)
-
-
(11)
-
Where the parallel quality factor, is equal to:
-
(12)
-
Similar to the series resonant circuit, we see that even though the currents through the reactances cancel out, the individual currents could be very large.