Difference between revisions of "Introduction to CoE 161"
Adrian Vidal (talk | contribs) |
|||
| (25 intermediate revisions by one other user not shown) | |||
| Line 120: | Line 120: | ||
Enumerating the sequence of 16 flips would give us <math>hhththhthhthhthh</math>, or using a '''1''' for <math>h</math> and '''0''' for <math>t</math>, we would get '''1101011011011011'''. Notice that <math>n</math> fair coin flips gives us <math>n</math> bits of information, and requires a binary word that is <math>n</math> digits long to describe. | Enumerating the sequence of 16 flips would give us <math>hhththhthhthhthh</math>, or using a '''1''' for <math>h</math> and '''0''' for <math>t</math>, we would get '''1101011011011011'''. Notice that <math>n</math> fair coin flips gives us <math>n</math> bits of information, and requires a binary word that is <math>n</math> digits long to describe. | ||
| + | |||
| + | === Another Example: Surprise! The Unexpected Observation === | ||
| + | Information can be thought of as the amount of ''surprise'' at seeing an event. Note that a highly probable outcome is not surprising. Consider the following events: | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! Event | ||
| + | ! Probability | ||
| + | ! Information (Surprise) | ||
| + | |- | ||
| + | |Someone tells you <math>1=1</math>. | ||
| + | |<math>1</math> | ||
| + | |<math>\log_2\left(1\right) = 0</math> | ||
| + | |- | ||
| + | | You got the wrong answer on a 4-choice multiple choice question. | ||
| + | |<math>\frac{3}{4}</math> | ||
| + | |<math>\log_2\left(\frac{4}{3}\right)=0.415\,\mathrm{bits}</math> | ||
| + | |- | ||
| + | | You guessed correctly on a 4-choice multiple choice question. | ||
| + | |<math>\frac{1}{4}</math> | ||
| + | |<math>\log_2\left(4\right)=2\,\mathrm{bits}</math> | ||
| + | |- | ||
| + | | You got the correct answer in a True or False question. | ||
| + | |<math>\frac{1}{2}</math> | ||
| + | |<math>\log_2\left(2\right)=1\,\mathrm{bit}</math> | ||
| + | |- | ||
| + | | You rolled a seven on rolling a pair of dice. | ||
| + | |<math>\frac{6}{36}</math> | ||
| + | |<math>\log_2\left(6\right)=2.58\,\mathrm{bits}</math> | ||
| + | |- | ||
| + | | Winning the Ultra Lotto 6/58 jackpot. | ||
| + | |<math>\frac{1}{40400000}</math> | ||
| + | |<math>\log_2\left(40400000\right)=25.27\,\mathrm{bits}</math> | ||
| + | |- | ||
| + | |} | ||
== Introducing Entropy == | == Introducing Entropy == | ||
| Line 148: | Line 183: | ||
=== Alternative Definition of Entropy === | === Alternative Definition of Entropy === | ||
| − | + | Let <math>X</math> be a discrete random variable taking values from a finite set <math>\mathcal{X} = \{x_1, x_2, \ldots, x_n\}</math> with the corresponding probability distribution is <math>P = \{p_1, p_2, \ldots, p_n\}</math>. For a given function <math>g</math>, the '''expected value''' of <math>g(X)</math> is given by: | |
| − | {{NumBlk|::|<math>\ | + | {{NumBlk|::|<math>\operatorname{E}[ g(X)]=\sum_{i=1}^n p_i \cdot g(x_i)</math>|{{EquationRef|12}}}} |
| − | + | If <math>X</math> is a continuous random variable with distribution <math>p\left(x\right)</math>, then the expected value of <math>g(X)</math> is given by: | |
| − | {{NumBlk|::|<math>\ | + | {{NumBlk|::|<math>\operatorname{E}[ g\left(X\right)]=\int p\left(x\right) \cdot g(x) dx</math>|{{EquationRef|13}}}} |
| − | Hence, for <math> | + | Hence, for <math>g(x_i) = \log\left(\tfrac{1}{p_i}\right)</math>1, or <math>\log\left(\tfrac{1}{p\left(x\right)}\right)</math>, we can see that: |
| − | {{NumBlk|::|<math>H\left(P\right) = \ | + | {{NumBlk|::|<math>H\left(P\right) = \operatorname{E}[ I\left(p\right)]</math>|{{EquationRef|14}}}} |
Thus, we can think of ''entropy'' of a probability distribution as the ''expected value'' of the ''information'' of the distribution. | Thus, we can think of ''entropy'' of a probability distribution as the ''expected value'' of the ''information'' of the distribution. | ||
| + | |||
| + | In this course, we mostly limit our discussion of information theory to discrete random variables due to some nuances when dealing with continuous random variables. In fact, Shannon thought it was natural to replace the summation to an integral in calculating entropy for continuous random variables, only to be later shown that such an update would be inconsistent with his axioms on entropy. | ||
| + | |||
| + | For a continuous random variable <math>X</math>, we define the ''differential entropy'' as | ||
| + | |||
| + | {{NumBlk|::|<math>H\left(P\right) = \int p(x) \log\left(\frac{1}{p(x)}\right)</math>|{{EquationRef|15}}}} | ||
| + | |||
| + | Unlike in the discrete case, differential entropy may in fact be negative, which violates Shannon's first assumption. | ||
== The Gibbs Inequality == | == The Gibbs Inequality == | ||
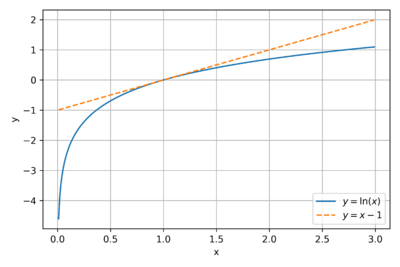
| − | [File:Gibbs Inequality.png|thumb| | + | [[File:Gibbs Inequality.png|thumb|400px|Figure 2: The plot of <math>y = \ln\left(x\right)</math> and <math>y = x - 1</math>.]] |
| − | Consider the natural logarithm function, <math>\ln\left(x\right)</math>. The slope of the the line tangent to <math>\ln\left(x\right)</math> at any point <math>x</math> is equal to <math>\tfrac{\partial \ln\left(x\right)}{\partial x}=\tfrac{1}{x}</math>. Thus, at <math>x=1</math>, the equation of the tangent line is <math>y=x-1</math>, as seen in Fig. 2. | + | |
| + | Consider the natural logarithm function, <math>\ln\left(x\right)</math>. The slope of the the line tangent to <math>\ln\left(x\right)</math> at any point <math>x</math> is equal to <math>\tfrac{\partial \ln\left(x\right)}{\partial x}=\tfrac{1}{x}</math>. Thus, at <math>x=1</math>, the equation of the tangent line is <math>y=x-1</math>, as seen in Fig. 2. Since <math>\ln\left(x\right)</math> is concave down, and for <math>x>0</math>, we get the following inequality: | ||
| + | |||
| + | {{NumBlk|::|<math>\ln\left(x\right) \leq x - 1</math>|{{EquationRef|15}}}} | ||
| + | |||
| + | The equality occurs when <math>x=1</math>. | ||
| + | |||
| + | For two probability distributions, <math>P=\{p_1, p_2, \ldots, p_n\}</math> and <math>Q=\{q_1, q_2, \ldots, q_n\}</math>, and using eq. 15, we get the '''Gibbs Inequality''': | ||
| + | |||
| + | {{NumBlk|::|<math>\sum_{i=1}^n p_i \ln\left(\frac{q_i}{p_i}\right) \leq \sum_{i=1}^n p_i \left(\frac{q_i}{p_i} -1 \right) = \sum_{i=1}^n \left(q_i - p_i\right) = \sum_{i=1}^n q_i - \sum_{i=1}^n p_i = 0</math>|{{EquationRef|16}}}} | ||
| + | |||
| + | This time, the equality occurs when <math>p_i = q_i</math> for all <math>i</math>. Though we derived the inequality for base <math>e</math>, it is straightforward to show that the inequality holds for any base. | ||
| + | |||
| + | Let's use the Gibbs Inequality to find the probability distribution that maximizes the entropy. For a probability distribution, <math>P=\{p_1, p_2, \ldots, p_n\}</math>: | ||
| + | |||
| + | {{NumBlk|::|<math>\begin{align}H\left(P\right) - \log_2\left(n\right) | ||
| + | & = \sum_{i=1}^n p_i\log_2\left(\frac{1}{p_i}\right)-\log_2\left(n\right) \\ | ||
| + | & = \sum_{i=1}^n p_i\log_2\left(\frac{1}{p_i}\right)-\log_2\left(n\right) \sum_{i=1}^n p_i \\ | ||
| + | & = \sum_{i=1}^n p_i\log_2\left(\frac{1}{p_i}\right) - \sum_{i=1}^n p_i \log_2\left(n\right) \\ | ||
| + | & = \sum_{i=1}^n p_i\left(\log_2\left(\frac{1}{p_i}\right) - \log_2\left(n\right)\right) \\ | ||
| + | & = \sum_{i=1}^n p_i\left(\log_2\left(\frac{1}{p_i}\right) + \log_2\left(\frac{1}{n}\right)\right) \\ | ||
| + | & = \sum_{i=1}^n p_i\log_2\left(\frac{\frac{1}{n}}{p_i}\right) \\ | ||
| + | & \leq 0 \\ | ||
| + | \end{align}</math>|{{EquationRef|17}}}} | ||
| + | |||
| + | Since <math>\sum_{i=1}^n\tfrac{1}{n} = 1</math>, we can use the Gibbs Inequality in obtaining the last step. Note that in this case, the equality occurs when <math>p_i = \tfrac{1}{n}</math>. | ||
| + | |||
| + | We can then rewrite eq. 17 as: | ||
| + | |||
| + | {{NumBlk|::|<math>0 \leq H\left(P\right) \leq \log_2\left(n\right)</math>|{{EquationRef|18}}}} | ||
| + | |||
| + | We can now look at the probability distributions at the upper and lower bounds of <math>H\left(P\right)</math>: | ||
| + | * At the lower bound, <math>H\left(P\right)=0</math> when one of the <math>p_i</math>'s is equal to 1, and the rest are all zero. | ||
| + | * At the upper bound, <math>H\left(P\right)=\log_2\left(n\right)</math> when <math>p_i = \tfrac{1}{n}</math> for all <math>i</math>. | ||
| + | |||
| + | Thus, the maximum of the entropy function is equal to <math>\log_2\left(n\right)</math>, where <math>n</math> is the number of all possible events, and occurs when all the events are equally likely. | ||
| + | |||
| + | === Example: Student Grades === | ||
| + | How much information can we get from a single grade? Note that the maximum entropy occurs when all the grades have equal probability. | ||
| + | * For Pass/Fail grades, the possible outcomes are: <math>\{\mathrm{P}, \mathrm{F}\}</math> with probabilities <math>\{\tfrac{1}{2}, \tfrac{1}{2}\}</math>. Thus, | ||
| + | |||
| + | {{NumBlk|::|<math>H\left(P\right)=\sum_{i=1}^n p_i\cdot \log_2\left(\frac{1}{p_i}\right) = \frac{1}{2}\cdot \log_2\left(2\right) + \frac{1}{2}\cdot \log_2\left(2\right) = 1\,\mathrm{bit}</math>|{{EquationRef|1}}}} | ||
| + | |||
| + | * For grades = <math>\{1.00, 2.00, 3.00, 4.00, 5.00\}</math> with probabilities <math>\{\tfrac{1}{5}, \tfrac{1}{5}, \tfrac{1}{5}, \tfrac{1}{5}, \tfrac{1}{5}\}</math>, we get: | ||
| + | |||
| + | {{NumBlk|::|<math>H\left(P\right)=\sum_{i=1}^n p_i\cdot \log_2\left(\frac{1}{p_i}\right) = 5\cdot \frac{1}{5}\cdot \log_2\left(5\right) = 2.32\,\mathrm{bits}</math>|{{EquationRef|2}}}} | ||
| + | |||
| + | * For grades = <math>\{1.00, 1.50, 2.00, 2.50, 3.00, 4.00, 5.00\}</math> with probabilities <math>\{\tfrac{1}{7}, \tfrac{1}{7}, \tfrac{1}{7}, \tfrac{1}{7}, \tfrac{1}{7}, \tfrac{1}{7}, \tfrac{1}{7}\}</math>, we have: | ||
| + | |||
| + | {{NumBlk|::|<math>H\left(P\right)=\sum_{i=1}^n p_i\cdot \log_2\left(\frac{1}{p_i}\right) = 7\cdot \frac{1}{7}\cdot \log_2\left(7\right) = 2.81\,\mathrm{bits}</math>|{{EquationRef|3}}}} | ||
| + | |||
| + | * If we have all the possible grades <math>\{1.00, 1.25, 1.50, 1.75, 2.00, 2.25, 2.50, 2.75, 3.00, 4.00, 5.00, \mathrm{INC}, \mathrm{DRP}, \mathrm{LOA}\}</math> with probabilities <math>\{\tfrac{1}{14}, \tfrac{1}{14}, \tfrac{1}{14}, \tfrac{1}{14}, \tfrac{1}{14}, \tfrac{1}{14}, \tfrac{1}{14}, \tfrac{1}{14}, \tfrac{1}{14}, \tfrac{1}{14}, \tfrac{1}{14}, \tfrac{1}{14}, \tfrac{1}{14}, \tfrac{1}{14}\}</math>, we have: | ||
| + | |||
| + | {{NumBlk|::|<math>H\left(P\right)=\sum_{i=1}^n p_i\cdot \log_2\left(\frac{1}{p_i}\right) = 14\cdot \frac{1}{14}\cdot \log_2\left(14\right) = 3.81\,\mathrm{bits}</math>|{{EquationRef|4}}}} | ||
| + | |||
| + | == Notes == | ||
| + | # These definitions of ''information'' and ''entropy'' might not be consistent with some other uses of the term. If a source transmits either the entire video of the ''Game of Thrones'' series, or the ''Lord of the Rings'' trilogy, and nothing else, then if we receive the entire ''Lord of the Rings'' trilogy, we get exactly one bit of information. | ||
| + | # Our definition of ''information'' and ''entropy'' depend only on the probability distribution. In general, it will not make sense to talk about the ''information'' or ''entropy'' of a source without specifying the probability distribution. It is possible for two observers to have to different models of the source, thus associating two different probability distributions to the source. If this happens, then the two observers will assign different values of ''information'' and ''entropy'' associated with the source. | ||
| + | |||
| + | {{Note|[[161-A1.1 | '''Activity A1.1''' Who is Claude Shannon?]] -- This activity introduces Claude Shannon, and given this introduction to information theory, asks us to imagine how this can affect the computer engineering field.|reminder}} | ||
== Sources == | == Sources == | ||
Latest revision as of 08:53, 24 February 2021
Welcome to CoE 161 / CoE 197!
Since we are offering this class remotely, there will be many changes to our normal course delivery:
- There will be no face-to-face lecture classes. All the material will be made available via this site.
- There will be more emphasis on student-centric activities, e.g. analysis, design, and simulations. Thus, you will be mostly "learning by doing". In this context, we will set aside an hour every week for consultations and questions via video-conferencing.
- Grades will be based on the submitted deliverables from the activities. Though we will not be very strict regarding the deadlines, it is a good idea to keep up with the class schedule and avoid cramming later in the semester.
Let's get started!
Contents
Measuring Complexity

For any system we are studying, designing, or building, an interesting and important question is usually: "How complex is this system?" or "How complex should this system be?". In general, we want to be able to compare two systems, and be able to say that one system is more complex than the other. In this case, having a numerical metric would be very convenient.
Possible ways of measuring complexity (obviously not a complete list!):
- Human observation, thus making any kind of rating subjective.
- Complexity based on the number of parts, components, or distinct elements. However, this depends on the definition of what is a "part". This is dependent on the observer's scale, from functional components down to atoms at the extreme case, as shown in Fig. 1.
- Number of dimensions. This is sometimes hard to measure, e.g. degrees of freedom, etc.
- Number of parameters controlling the system.
- The minimal description needed. However, we need to figure out which language we need to use.
- Information content. We then need to figure out how to define and measure information.
- Minimum generator or constructor (to build the system). We need to define what tools and methods we need to use to build the system.
- Minimum energy and/or time to construct the system. However, some systems evolve with time, so defining the beginning and end points can be difficult.
All of these measures are associated with a model of the system in question. Thus observers could use different models, and therefore come up with different notions of the complexity of the said system. We do not expect to come up with a single universal measure of complexity, but we can explore a framework that is optimal for (a) a particular observer, (b) a particular context, and (c) a particular purpose. Let us focus on the measures related to how unexpected an observation is, an approach known as Information Theory.
Some of the ideas and concepts that follow are based on basic probability ideas. You can review them here: Probability Review I.
The Basics of Information Theory
We want to create a metric for measuring the information we get from observing the occurrence of an event that has a probability . Let us ignore all other features of the event, except whether the event occurred or not. We can then think of the event as seeing if a symbol, whose probability of occurring is , appears. Thus, our definition of information is in terms of the probability .
An Axiomatic Approach
Let us define our information measure as . We want to have several properties:
| Axiom | Implied Property |
|---|---|
|
Information is a non-negative quantity. |
|
|
If an event has a , then we get no information from the occurrence of that event. |
|
|
If two independent events occur, then the information we get from observing the two events is the sum of the two 'informations'. |
|
|
is a continuous and monotonic function of the probability . |
Using these properties, we can then derive the following expressions:
-
(1)
-
Thus, by induction:
-
(2)
-
We can then write , or equivalently:
-
(3)
-
In general, we get:
-
(4)
-
Since is continuous, and for and for a real number , we get:
-
(5)
-
From this, and by inspection, we can express , for some base as:
-
(5)
-
Note that:
-
(6)
-
Thus, we can easily change the base of the logarithm, and the resulting information measure are differ by just a multiplicative constant, and have the following units:
| b | Units |
|---|---|
| 2 | bits (from binary) |
| 3 | trits (from trinary) |
| nats (from natural logarithm) | |
| 10 | Hartleys |
By default, and unless specified, we will be using , so when we write , we mean .
A Simple Example
If we flip a fair coin, we will get two possible events: , with probabilities . Thus, a one coin flip gives us bit of information, regardless of the result ( or ).
If we flip the coin times, or equivalently, if we flip coins at the same time, the amount of information (in bits) that we would get is equal to:
-
(7)
-
Enumerating the sequence of 16 flips would give us , or using a 1 for and 0 for , we would get 1101011011011011. Notice that fair coin flips gives us bits of information, and requires a binary word that is digits long to describe.
Another Example: Surprise! The Unexpected Observation
Information can be thought of as the amount of surprise at seeing an event. Note that a highly probable outcome is not surprising. Consider the following events:
| Event | Probability | Information (Surprise) |
|---|---|---|
| Someone tells you . | ||
| You got the wrong answer on a 4-choice multiple choice question. | ||
| You guessed correctly on a 4-choice multiple choice question. | ||
| You got the correct answer in a True or False question. | ||
| You rolled a seven on rolling a pair of dice. | ||
| Winning the Ultra Lotto 6/58 jackpot. |
Introducing Entropy
Consider a source generating a stream of symbols. If there are distinct symbols, , and the source emits these symbols with probabilities respectively. Let us assume that the symbols are emitted independently, e.g. the emitted symbol does not depend on past symbols.
If we observe the symbol , we get bits of information from that particular observation.
For observations, the symbol would occur approximately times. Therefore, if we have independent observations, the total information, , that we will get is:
-
(8)
-
The average information that we get per symbol that we observe would then be equal to:
-
(9)
-
Note that since , we will define when .
The Definition of Entropy
Given a discrete probability distribution , the entropy of the distribution is:
-
(10)
-
For a continuous probability distribution, , entropy is defined as:
-
(11)
-
This definition was introduced by Claude Shannon in his landmark 1948 paper[1]. For more information on the life of Claude Shannon, you can read this article[2], or watch this documentary film[3].
Alternative Definition of Entropy
Let be a discrete random variable taking values from a finite set with the corresponding probability distribution is . For a given function , the expected value of is given by:
-
(12)
-
If is a continuous random variable with distribution , then the expected value of is given by:
-
(13)
-
Hence, for 1, or , we can see that:
-
(14)
-
Thus, we can think of entropy of a probability distribution as the expected value of the information of the distribution.
In this course, we mostly limit our discussion of information theory to discrete random variables due to some nuances when dealing with continuous random variables. In fact, Shannon thought it was natural to replace the summation to an integral in calculating entropy for continuous random variables, only to be later shown that such an update would be inconsistent with his axioms on entropy.
For a continuous random variable , we define the differential entropy as
-
(15)
-
Unlike in the discrete case, differential entropy may in fact be negative, which violates Shannon's first assumption.
The Gibbs Inequality
Consider the natural logarithm function, . The slope of the the line tangent to at any point is equal to . Thus, at , the equation of the tangent line is , as seen in Fig. 2. Since is concave down, and for , we get the following inequality:
-
(15)
-
The equality occurs when .
For two probability distributions, and , and using eq. 15, we get the Gibbs Inequality:
-
(16)
-
This time, the equality occurs when for all . Though we derived the inequality for base , it is straightforward to show that the inequality holds for any base.
Let's use the Gibbs Inequality to find the probability distribution that maximizes the entropy. For a probability distribution, :
-
(17)
-
Since , we can use the Gibbs Inequality in obtaining the last step. Note that in this case, the equality occurs when .
We can then rewrite eq. 17 as:
-
(18)
-
We can now look at the probability distributions at the upper and lower bounds of :
- At the lower bound, when one of the 's is equal to 1, and the rest are all zero.
- At the upper bound, when for all .
Thus, the maximum of the entropy function is equal to , where is the number of all possible events, and occurs when all the events are equally likely.
Example: Student Grades
How much information can we get from a single grade? Note that the maximum entropy occurs when all the grades have equal probability.
- For Pass/Fail grades, the possible outcomes are: with probabilities . Thus,
-
(1)
-
- For grades = with probabilities , we get:
-
(2)
-
- For grades = with probabilities , we have:
-
(3)
-
- If we have all the possible grades with probabilities , we have:
-
(4)
-
Notes
- These definitions of information and entropy might not be consistent with some other uses of the term. If a source transmits either the entire video of the Game of Thrones series, or the Lord of the Rings trilogy, and nothing else, then if we receive the entire Lord of the Rings trilogy, we get exactly one bit of information.
- Our definition of information and entropy depend only on the probability distribution. In general, it will not make sense to talk about the information or entropy of a source without specifying the probability distribution. It is possible for two observers to have to different models of the source, thus associating two different probability distributions to the source. If this happens, then the two observers will assign different values of information and entropy associated with the source.
































































![{\displaystyle \operatorname {E} [g(X)]=\sum _{i=1}^{n}p_{i}\cdot g(x_{i})}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f9205e5ea73462957607566f934fdef4b2e2b250)

![{\displaystyle \operatorname {E} [g\left(X\right)]=\int p\left(x\right)\cdot g(x)dx}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/94f7faa188e9f6b36319512ad749bd39a62a3402)


![{\displaystyle H\left(P\right)=\operatorname {E} [I\left(p\right)]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/b87f1dd2680eb4a679e89ed56c7a9f87e3d9ad72)