Difference between revisions of "CoE 197U MOS Differential Pairs"
| Line 56: | Line 56: | ||
Beyond <math>|V_{id,max}|</math> the currents rail, and therefore, the differential output voltage also rail. Fig. 7 also shows that the amplifier has an inverting gain. | Beyond <math>|V_{id,max}|</math> the currents rail, and therefore, the differential output voltage also rail. Fig. 7 also shows that the amplifier has an inverting gain. | ||
| − | == Small Signal AC and Half Circuit Analysis == | + | == Small-Signal AC and Half Circuit Analysis == |
| + | Taking the limit as <math>V_{id}\{rightarrow}0</math>, it can be shown that the <math>v_{od}(v_{id})</math> approaches a linear function, and the small-signal gain is <math>-g_mR_D </math> which must be very familiar. Note that this <math>g_m</math> is evaluated at the case where <math>V_{id}</math> is around 0, where <math>I_{D1}\approx I_{D2}\approx \frac{I_T}{2}</math>, and that the small-signal gain represents the slope of the <math>V_{od}</math> vs. <math>V_{id}</math> plot for very small <math>V_{id}</math>. The expression is not very accurate because Eqs. 4 and 5 assumes that <math>r_o</math> is very large. | ||
| + | |||
| + | ::<math>A_{dm}=\frac{v_{od}}{v_{id}}=\left.\frac{\partial V_{od}}{\partial V_{id}}\right|_{V_{id}\rightarrow 0}</math> | ||
| + | ::<math>A_{dm}\approx -R_D\frac{k'}{2}\frac{W}{L}\sqrt{\frac{4I_T}{k'\frac{W}{L}}}</math> | ||
| + | {{NumBlk|::|<math>A_{dm}\approx -R_D\sqrt{2k'\frac{W}{L}\left(\frac{I_T}{2}\right)} = -R_D\sqrt{2k'\frac{W}{L}I_{D1}} = -R_D\sqrt{2k'\frac{W}{L}I_{D2}} = -g_mR_D</math>|{{EquationRef|5}}}} | ||
| + | |||
| + | Eq. 5 shows that the small-signal differential gain is dependent only on Rd, the transistor dimensions, and the tail current. Changing the DC bias of the input voltage will not affect the gain as long as the transistors are saturated and the tail current is fixed. | ||
| + | |||
| + | Analyzing the circuit’s small-signal model will help determine the small-signal gains easier, without having to assume that <math>r_o\rightarrow \infty</math>. The full small-signal equivalent circuit is shown in Fig. 8. Here we are assuming that the tail current source is non-ideal and has some finite small-signal resistance <math>r_{tail}</math>. Note also, that transistors’ <math>r_o</math> are maintained. | ||
| + | |||
| + | [[File:Small signal equivalent circuit of the MOS differential amplifier with resistor load.png|thumb|600px|center|Figure 8: Small-signal equivalent circuit of the MOS differential amplifier with resistor load]] | ||
| + | |||
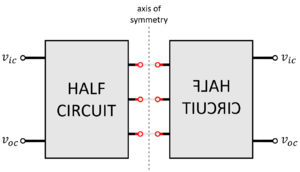
| + | The differential gain <math>A_{dm}</math> is analyzed with <math>v_{ic}=0</math>. If the circuit is perfectly balanced, it follows that <math>v_{oc}=0</math>. Due to symmetry, analyzing only half of the circuit should already give us enough information. With differential inputs only in play, one side/half can be considered “positive” while the other side/half can be considered “negative.” Thus, the middle point/s of the differential circuit must be at small-signal 0V. We can divide the circuit in half and place a virtual differential ground at each wire that is cut by the axis of symmetry. Note, however, that we must still maintain the voltage definitions with <math>v_{ic}=0</math> (i.e. <math>v_{i1}</math> remains <math>+\frac{v_{id}}{2}</math>, etc.) as in Fig. 9. | ||
| + | |||
| + | {| style="margin-left: auto; margin-right: auto; border: none; width: 75%;" | ||
| + | |- | ||
| + | | [[File:Determining the differential half circuit.png|thumb|center|Figure 9: Determining the differential half circuit ]] || | ||
| + | [[File:Differential half circuit of the differential pair with resistor load.png|thumb|center|Figure 10: Differential half circuit of the differential pair with resistor load]] | ||
| + | |} | ||
| + | |||
| + | Taking the left-side of Fig. 8 for the differential half circuit analysis, we end up with Fig. 10. Note that the voltages are still <math>+\frac{v_{id}}{2}</math> and <math>+\frac{v_{od}}{2}</math>. The tail resistance was also divided into two <math>2\cdot r_{tail}</math>’s to properly cut the circuit in half. The source is at (differential) ground, and thus, <math>r_{tail}</math> is effectively shorted. The remaining portion of the half circuit resembles that of a resistor-loaded common source, whose gain is <math>-g_m\left(r_o||R_D\right)</math>. However, the input is <math>\frac{v_{id}}{2}</math> while the output is <math>\frac{v_{od}}{2}</math>. Thus, this gain is given by: | ||
| + | |||
| + | ::<math>\frac{v_{od}/2}{v_{id}/2}=-g_m\left(r_o||R_L\right)</math> | ||
| + | {{NumBlk|::|<math>A_{dm}=\frac{v_{od}}{v_{id}}=-g_m\left(r_o||R_L\right)</math>|{{EquationRef|6}}}} | ||
| + | |||
| + | For the common-mode case, <math>v_{id}</math> must be set to zero which consequently makes <math>v_{od}=0</math>. This time, since we are applying common or the same excitation on both sides of a balanced circuit then, there must be no current flowing either from left to right or from right to left since the two sides are at the same potential. Thus, portions that are cut in dividing the circuit into two are left open, instead of placing a ground, as shown in Fig. 11. The common-mode half circuit is shown in Fig. 12. This circuit follows the same structure as a common source amplifier with emitter degeneration, and with <math>R_C=R_L</math> and <math>R_E=2r_{tail}</math>. The gain of such a circuit is approximately <math>\frac{-g_mR_C}{1+g_mR_E}</math>. Thus, the common-mode gain is given by Eq. 7. Note that if the current source were ideal, then <math>r_{tail}\rightarrow \infty</math> and <math>A_{cm}\rightarrow 0</math>. | ||
| + | |||
| + | {{NumBlk|::|<math>A_{cm}\approx\frac{v_{oc}}{v_{ic}}=-\frac{g_mR_L}{1+g_m\cdot 2r_{tail}}</math>|{{EquationRef|7}}}} | ||
| + | |||
| + | {| style="margin-left: auto; margin-right: auto; border: none; width: 75%;" | ||
| + | |- | ||
| + | | [[File:Determining the common-mode half circuit.png|thumb|center|Figure 11: Determining the common-mode half circuit]] || | ||
| + | [[File:Common-mode half circuit of the differential pair with resistor load.png|thumb|center|Figure 12: Common-mode half circuit of the differential pair with resistor load]] | ||
| + | |} | ||
| + | |||
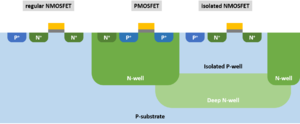
| + | Note that the previous expression is valid only when there is '''no''' body effect. However, this is not true for the circuit in Fig. 6 since the body is grounded while the source is not. In a standard CMOS technology with a p-type substrate, shorting the PMOS source to its body is easy since each PMOS has its own n-well. However, for NMOS, the body is also the substrate that is shared across the whole chip. It will only be possible to short the NMOS source to the body, without shorting the rest of the substrate, if the technology has a way to isolate and tap an NMOS’s p-type body from the rest of the chip. Such a feat is possible with a ''triple well'' technology (Fig. 13). | ||
| + | |||
| + | [[File:Transistors in a triple-well technology.png|thumb|center|Figure 13: Transistors in a triple-well technology]] | ||
| + | |||
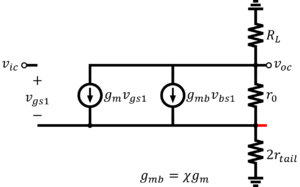
| + | If the body is not or cannot be tied to the source, then the body effect occurs, where changes in <math>v_{BS}</math> cause threshold voltage to change. Thus, when the source potential changes, the drain current changes not only because <math>v_{GS}</math> changes but also because the threshold voltage changes. The small-signal common-mode half circuit with the body effect is shown in Fig. 14. Analysis of this half circuit will lead to a common-mode gain expressed by Eq. 8. Note that the body transconductance is given by <math>g_{mb}=\chi g_m</math> | ||
| + | |||
| + | {{NumBlk|::|<math>A_{cm}\approx -\frac{g_m}{1+g_m\left(1+\chi\right)\cdot 2r_{tail}}\cdot R_L||\left(r_o+2r_{tail}+g_m\left(1+\chi\right)r_o\cdot 2r_{tail}\right)</math>|{{EquationRef|8}}}} | ||
| + | |||
| + | [[File:Common-mode half circuit of the resistor-loaded differential pair with body effect.png|thumb|center|Figure 14: Common-mode half circuit of the resistor-loaded differential pair with body effect]] | ||
| + | |||
| + | Note that there is no body effect in the differential circuit even if the source not shorted to the body since the bulk is grounded and the source is at the differential ground. Thus, the small-signal <math>v_{bs}</math> is 0. | ||
| + | |||
=== CMRR === | === CMRR === | ||
| + | |||
| + | {{NumBlk|::|<math>CMRR=\left|\frac{A_{dm}}{A_{cm}}\right|</math>|{{EquationRef|9}}}} | ||
| + | |||
| + | The common-mode rejection ratio or CMRR is given by Eq. 9. CMRR is a primary figure of merit for differential amplifiers. The higher the CMRR, the better. For the differential pair with body effect, the CMRR is approximately given by Eq. 10. The CMRR of the differential amplifier improves with increasing <math>r_{tail}</math> and is independent of the load resistance. The equation also shows that the body effect helps improve CMRR since χ is a positive quantity typically around 0.1 to 0.3. Although the body-effect improves CMRR by reducing Acm, it must be noted that the body effect still influences the threshold voltage and can impact the allowable DC voltage levels and signal swing. | ||
| + | |||
| + | ::<math>A_{cm}\approx -\frac{g_mR_L}{1+g_m\left(1+\chi\right)\cdot 2r_{tail}}</math> | ||
| + | {{NumBlk|::|<math>CMRR \approx 1+g_m\left(1+\chi\right)\cdot 2r_{tail}</math>|{{EquationRef|10}}}} | ||
| + | |||
== Differential Pair with Active Load == | == Differential Pair with Active Load == | ||
== Differential to Single-Ended Output Conversion == | == Differential to Single-Ended Output Conversion == | ||
Revision as of 16:12, 15 April 2021
The differential pair is one of the most commonly used circuit blocks in analog IC design. It enables amplifiers to have not just two, but specifically, differential inputs and act based only or mostly on the difference of the input signals.
The main references for this topic are chapters 3.5 and 4.3.5 of the Analysis and Design of Analog Integrated Circuits book.
Contents
Fully Differential Amplifier Signal and Gain Definitions
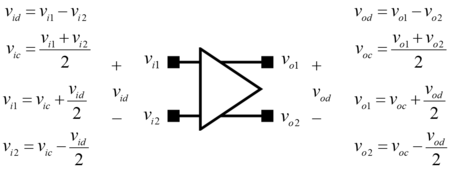
Before proceeding, the voltage signals to be dealt with need to be defined first to aid in the discussion. We will look at a general fully differential amplifier with a differential input and a differential output. The differential input/output voltages are the difference of input/output voltages. The common-mode input/output voltages are the average of the input/output voltages. Given how , , , and are related (Fig. 1), knowledge of any two can be used to infer the remaining two.
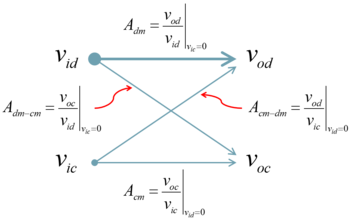
The presence of differential and common-mode inputs and outputs require a clarification on how the gains are defined (Fig. 2). An ideal fully differential amplifier will have a very large and very low , as the arrows' thickness suggests. and are also ideally very low. and are both zero if the circuit is perfectly balanced, which requires that components are perfectly matched in terms of device properties and bias.
The advantage of having a differential input is the ability to reject signals that are common to both inputs such as noise that is coupled to both input signals. As can be seen in Fig. 3, the noise present on both inputs, and , does not appear at the differential signal . If indeed the differential pair works only on this differential input signal, then the noise will not be amplified with the actual input information. The same property also allows the circuit to be less sensitive to the DC offset of the two signals. This makes differential amplifiers easy to cascade without the need for AC-coupling capacitors, which generally need to be large and are costly in IC implementations. However, care is still needed when dealing with large signal swings and/or small supply voltages.
DC and Large Signal Analysis
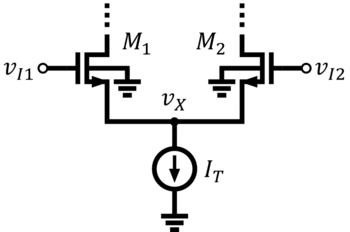
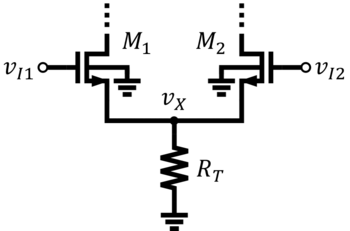
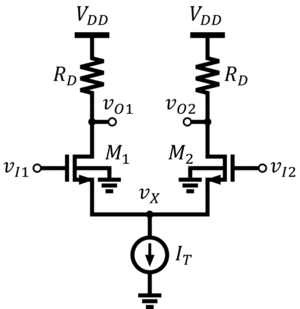
The MOS differential pair or the source-coupled pair is shown in Figs. 4a and 4b. In source-coupled pairs, the source nodes are tied together. The current source is referred to as the tail current source. A simple but crude way of providing current to the differential pair is by using a tail resistor instead of a current source.
Assume that the transistors are perfectly matched/identical. Assume also that anything connected above the drain terminals are perfectly balanced or symmetric. For the DC analysis, assume that for simplicity to highlight the basic operation of the circuit.
Consider the differential pair with a tail current source (Fig. 4a). When there is no differential input, then the input voltages and must exactly be equal at some common-mode voltage . By virtue of symmetry, the transistors must have the same current, i.e. . Such is the case without even taking note of what is the actual . If should change, adjusts to maintain the Vgs that corresponds to . Since can be inferred from the transistor dimensions and the DC current, which are both constant, then is maintained even if changes, again, under the assumption that or is very large.
The large signal characteristics of the MOS differential pair analysis is started by setting up a KVL equation from to and relating it to currents and , under the restriction that . The following equations are valid given that the two transistors are saturated.
- For :
-
(1)
-
-
(2)
-
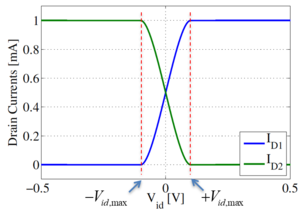
When , all of will flow only through one transistor while the other transistor will be in cut-off. This is shown in Fig. 5. Thus, the tail current is effectively steered or distributed between M1 and M2 by , regardless of the as long as the transistors are saturated and the current source is still operating as intended.
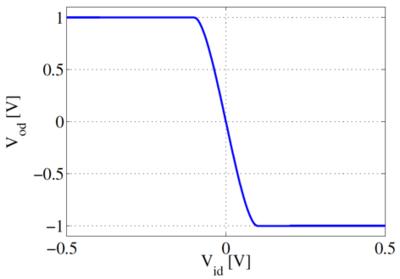
Assuming that the load is a pair of equal and matched resistors such in Fig. 6, the output voltage is determined by KVL (Eq. 3) and the difference in drain currents (Eqs. 1 and 2). The resulting expression is Eq. 4. The plot of this function is the middle portion of Fig. 7.
-
(3)
-
- For :
-
(4)
-
Beyond the currents rail, and therefore, the differential output voltage also rail. Fig. 7 also shows that the amplifier has an inverting gain.
Small-Signal AC and Half Circuit Analysis
Taking the limit as , it can be shown that the approaches a linear function, and the small-signal gain is which must be very familiar. Note that this is evaluated at the case where is around 0, where , and that the small-signal gain represents the slope of the vs. plot for very small . The expression is not very accurate because Eqs. 4 and 5 assumes that is very large.
-
(5)
-
Eq. 5 shows that the small-signal differential gain is dependent only on Rd, the transistor dimensions, and the tail current. Changing the DC bias of the input voltage will not affect the gain as long as the transistors are saturated and the tail current is fixed.
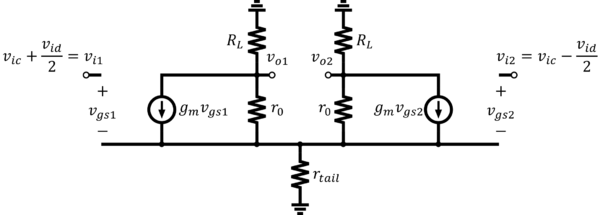
Analyzing the circuit’s small-signal model will help determine the small-signal gains easier, without having to assume that . The full small-signal equivalent circuit is shown in Fig. 8. Here we are assuming that the tail current source is non-ideal and has some finite small-signal resistance . Note also, that transistors’ are maintained.
The differential gain is analyzed with . If the circuit is perfectly balanced, it follows that . Due to symmetry, analyzing only half of the circuit should already give us enough information. With differential inputs only in play, one side/half can be considered “positive” while the other side/half can be considered “negative.” Thus, the middle point/s of the differential circuit must be at small-signal 0V. We can divide the circuit in half and place a virtual differential ground at each wire that is cut by the axis of symmetry. Note, however, that we must still maintain the voltage definitions with (i.e. remains , etc.) as in Fig. 9.
Taking the left-side of Fig. 8 for the differential half circuit analysis, we end up with Fig. 10. Note that the voltages are still and . The tail resistance was also divided into two ’s to properly cut the circuit in half. The source is at (differential) ground, and thus, is effectively shorted. The remaining portion of the half circuit resembles that of a resistor-loaded common source, whose gain is . However, the input is while the output is . Thus, this gain is given by:
-
(6)
-
For the common-mode case, must be set to zero which consequently makes . This time, since we are applying common or the same excitation on both sides of a balanced circuit then, there must be no current flowing either from left to right or from right to left since the two sides are at the same potential. Thus, portions that are cut in dividing the circuit into two are left open, instead of placing a ground, as shown in Fig. 11. The common-mode half circuit is shown in Fig. 12. This circuit follows the same structure as a common source amplifier with emitter degeneration, and with and . The gain of such a circuit is approximately . Thus, the common-mode gain is given by Eq. 7. Note that if the current source were ideal, then and .
-
(7)
-
Note that the previous expression is valid only when there is no body effect. However, this is not true for the circuit in Fig. 6 since the body is grounded while the source is not. In a standard CMOS technology with a p-type substrate, shorting the PMOS source to its body is easy since each PMOS has its own n-well. However, for NMOS, the body is also the substrate that is shared across the whole chip. It will only be possible to short the NMOS source to the body, without shorting the rest of the substrate, if the technology has a way to isolate and tap an NMOS’s p-type body from the rest of the chip. Such a feat is possible with a triple well technology (Fig. 13).
If the body is not or cannot be tied to the source, then the body effect occurs, where changes in cause threshold voltage to change. Thus, when the source potential changes, the drain current changes not only because changes but also because the threshold voltage changes. The small-signal common-mode half circuit with the body effect is shown in Fig. 14. Analysis of this half circuit will lead to a common-mode gain expressed by Eq. 8. Note that the body transconductance is given by
-
(8)
-
Note that there is no body effect in the differential circuit even if the source not shorted to the body since the bulk is grounded and the source is at the differential ground. Thus, the small-signal is 0.
CMRR
-
(9)
-
The common-mode rejection ratio or CMRR is given by Eq. 9. CMRR is a primary figure of merit for differential amplifiers. The higher the CMRR, the better. For the differential pair with body effect, the CMRR is approximately given by Eq. 10. The CMRR of the differential amplifier improves with increasing and is independent of the load resistance. The equation also shows that the body effect helps improve CMRR since χ is a positive quantity typically around 0.1 to 0.3. Although the body-effect improves CMRR by reducing Acm, it must be noted that the body effect still influences the threshold voltage and can impact the allowable DC voltage levels and signal swing.
-
(10)
-