Difference between revisions of "Chebyshev Filters"
| (7 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | Chebyshev filters come in two flavors: the Type-I and Type-II. | + | Chebyshev filters come in two flavors: the more popular Type-I and the Type-II Chebyshev filter. |
== The Chebyshev Type-I Low-Pass Filter == | == The Chebyshev Type-I Low-Pass Filter == | ||
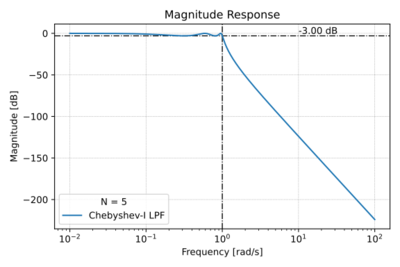
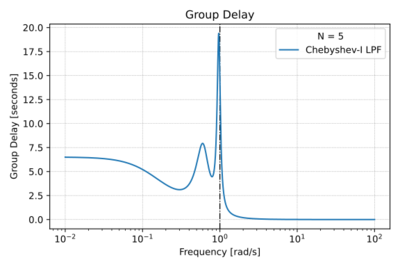
| − | Chebyshev Type-I filters are also ''all-pole filters'', with poles of the normalized (<math>\omega_0 = 1\,\mathrm{\tfrac{rad}{s}}</math>) filter located on an ellipse inside the unit circle. This arrangement of poles results in (1) a shorter transition band, and therefore a steeper roll-off compared to the Butterworth low-pass filter of the same order, (2) poorer group delay characteristics, and (3) ripples in the pass-band. By allowing larger ripples in the pass-band, we get: (1) a narrower transition band, and hence sharper cut-off, (2) higher Q poles, and (3) more degradation in the phase response. | + | Chebyshev Type-I filters are also ''all-pole filters'', with poles of the normalized (<math>\omega_0 = 1\,\mathrm{\tfrac{rad}{s}}</math>) filter located on an ellipse inside the unit circle, as shown in Fig. 1. This arrangement of poles results in (1) a shorter transition band, and therefore a steeper roll-off compared to the Butterworth low-pass filter of the same order, shown in Fig. 2, (2) poorer group delay characteristics as depicted in Figs. 3 and 4, and (3) ripples in the pass-band also seen in Fig. 2. By allowing larger ripples in the pass-band, we get: (1) a narrower transition band, and hence sharper cut-off, (2) higher Q poles, and (3) more degradation in the phase response. |
{| | {| | ||
| − | |[[File:Cheby1 pz plot.svg|thumb|400px|Figure 1: The Chebyshev Type-I pole-zero with <math>N=5</math> and a <math>3\,\text{dB}</math> ripple.]] | + | |[[File:Cheby1 pz plot.svg|thumb|400px|Figure 1: The low-pass Chebyshev Type-I pole-zero with <math>N=5</math> and a <math>3\,\text{dB}</math> ripple.]] |
| − | |[[File:Cheby1 mag.svg|thumb|400px|Figure 2: The Chebyshev Type-I low-pass filter magnitude response with <math>N=5</math> and a <math>3\,\text{dB}</math> ripple.]] | + | |[[File:Cheby1 mag.svg|thumb|400px|Figure 2: The low-pass Chebyshev Type-I low-pass filter magnitude response with <math>N=5</math> and a <math>3\,\text{dB}</math> ripple.]] |
|- | |- | ||
| − | |[[File:Cheby1 phase.svg|thumb|400px|Figure 3: The Chebyshev Type-I low-pass filter phase response with <math>N=5</math> and a <math>3\,\text{dB}</math> ripple.]] | + | |[[File:Cheby1 phase.svg|thumb|400px|Figure 3: The low-pass Chebyshev Type-I low-pass filter phase response with <math>N=5</math> and a <math>3\,\text{dB}</math> ripple.]] |
| − | |[[File:Cheby1 group delay.svg|thumb|400px|Figure 4: The Chebyshev Type-I low-pass filter group delay with <math>N=5</math> and a <math>3\,\text{dB}</math> ripple.]] | + | |[[File:Cheby1 group delay.svg|thumb|400px|Figure 4: The low-pass Chebyshev Type-I low-pass filter group delay with <math>N=5</math> and a <math>3\,\text{dB}</math> ripple.]] |
|} | |} | ||
| Line 18: | Line 18: | ||
</math>|{{EquationRef|1}}}} | </math>|{{EquationRef|1}}}} | ||
| − | Where <math>\omega_0</math> is the cut-off frequency, <math>\varepsilon=\sqrt{10^\frac{\delta}{10}-1}</math> is the ripple factor with ripple <math>\delta</math> in dB, and <math>T_N\left(x\right)</math> are solutions to the Chebyshev differential equation: | + | Where <math>N</math> is the filter order, <math>\omega_0</math> is the cut-off frequency, <math>\varepsilon=\sqrt{10^\frac{\delta}{10}-1}</math> is the ripple factor with ripple <math>\delta</math> in dB, and <math>T_N\left(x\right)</math> are solutions to the Chebyshev differential equation: |
{{NumBlk|::|<math> | {{NumBlk|::|<math> | ||
| Line 24: | Line 24: | ||
</math>|{{EquationRef|2}}}} | </math>|{{EquationRef|2}}}} | ||
| − | For a normalized filter, or <math>\omega_0 = 1\,\mathrm{\tfrac{rad}{s}}</math>, the poles of the Chebyshev Type-I low-pass filter are the roots of <math>1+\varepsilon^2\cdot T_N^2\left(-js\right)=0</math>. In practice, instead of solving this equation directly, we can easily get the roots (and hence the poles) of the filter | + | For a normalized filter, or <math>\omega_0 = 1\,\mathrm{\tfrac{rad}{s}}</math>, the poles of the Chebyshev Type-I low-pass filter are the roots of <math>1+\varepsilon^2\cdot T_N^2\left(-js\right)=0</math>. In practice, instead of solving this equation directly, we can easily get the roots (and hence the poles) of the filter transfer function using tools such as Python or Matlab. |
== The Chebyshev Type-II Low-Pass Filter == | == The Chebyshev Type-II Low-Pass Filter == | ||
| + | The Chebyshev Type-II filter of order <math>N</math> has <math>N</math> poles and <math>N</math> zeros for even <math>N</math>, and <math>N-1</math> zeros for odd <math>N</math>. It has poles inside and outside the unit circuit, and complex conjugate zeros on the <math>j\omega</math>-axis, creating ''nulls'' in the stop-band. It is also less common than the Type-I filter since the roll-off is less steep, and due to its zeros, it requires more components. | ||
| + | |||
| + | The Chebyshev Type-II magnitude response is given by: | ||
| + | |||
| + | {{NumBlk|::|<math> | ||
| + | \left|H\left(j\omega\right)\right| = \frac{1}{\sqrt{1+ \frac{1}{\varepsilon^2\cdot T_N^2\left(\frac{\omega}{\omega_0}\right)}}} | ||
| + | </math>|{{EquationRef|3}}}} | ||
| + | |||
| + | Where <math>N</math> is the filter order, <math>\omega_0</math> is the cut-off frequency, and <math>\varepsilon=\sqrt{10^\frac{\gamma}{10}-1}</math> is the attenuation factor with stop-band attenuation <math>\gamma</math> in dB. The poles are the roots of: | ||
| + | |||
| + | {{NumBlk|::|<math> | ||
| + | 1+\varepsilon^2T_N^2\left(-\frac{1}{js}\right)=0 | ||
| + | </math>|{{EquationRef|4}}}} | ||
| + | |||
| + | And the zeros are given by: | ||
| + | |||
| + | {{NumBlk|::|<math> | ||
| + | \frac{1}{z_m} = -j\cos\left(\frac{\pi}{2}\cdot \frac{2m-1}{N}\right) | ||
| + | </math>|{{EquationRef|5}}}} | ||
| + | |||
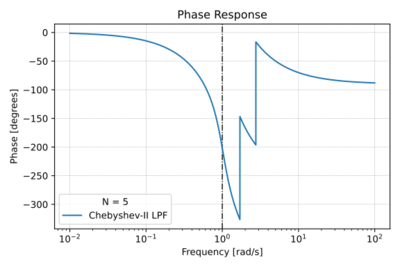
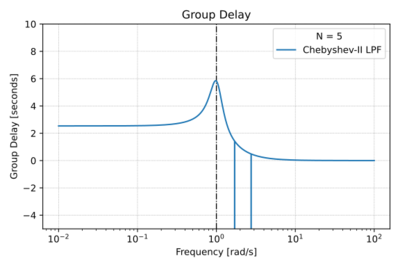
| + | For <math>m=1,2,\ldots, N</math>. The characteristics of the Chebyshev Type-II filter are shown in Figs. 1-4. | ||
| + | |||
| + | {| | ||
| + | |[[File:Cheby2 pz plot.svg|thumb|400px|Figure 1: The low-pass Chebyshev Type-II pole-zero with <math>N=5</math> and a <math>40\,\text{dB}</math> stop-band attenuation.]] | ||
| + | |[[File:Cheby2 mag.svg|thumb|400px|Figure 2: The low-pass Chebyshev Type-II magnitude response with <math>N=5</math> and a <math>40\,\text{dB}</math> stop-band attenuation.]] | ||
| + | |- | ||
| + | |[[File:Cheby2 phase.svg|thumb|400px|Figure 3: The low-pass Chebyshev Type-II phase response with <math>N=5</math> and a <math>40\,\text{dB}</math> stop-band attenuation.]] | ||
| + | |[[File:Cheby2 group delay.svg|thumb|400px|Figure 4: The low-pass Chebyshev Type-II group delay with <math>N=5</math> and a <math>40\,\text{dB}</math> stop-band attenuation.]] | ||
| + | |- | ||
| + | |} | ||
Latest revision as of 11:23, 18 March 2021
Chebyshev filters come in two flavors: the more popular Type-I and the Type-II Chebyshev filter.
The Chebyshev Type-I Low-Pass Filter
Chebyshev Type-I filters are also all-pole filters, with poles of the normalized () filter located on an ellipse inside the unit circle, as shown in Fig. 1. This arrangement of poles results in (1) a shorter transition band, and therefore a steeper roll-off compared to the Butterworth low-pass filter of the same order, shown in Fig. 2, (2) poorer group delay characteristics as depicted in Figs. 3 and 4, and (3) ripples in the pass-band also seen in Fig. 2. By allowing larger ripples in the pass-band, we get: (1) a narrower transition band, and hence sharper cut-off, (2) higher Q poles, and (3) more degradation in the phase response.
The Chebyshev Type-I magnitude response is given by:
-
(1)
-
Where is the filter order, is the cut-off frequency, is the ripple factor with ripple in dB, and are solutions to the Chebyshev differential equation:
-
(2)
-
For a normalized filter, or , the poles of the Chebyshev Type-I low-pass filter are the roots of . In practice, instead of solving this equation directly, we can easily get the roots (and hence the poles) of the filter transfer function using tools such as Python or Matlab.
The Chebyshev Type-II Low-Pass Filter
The Chebyshev Type-II filter of order has poles and zeros for even , and zeros for odd . It has poles inside and outside the unit circuit, and complex conjugate zeros on the -axis, creating nulls in the stop-band. It is also less common than the Type-I filter since the roll-off is less steep, and due to its zeros, it requires more components.
The Chebyshev Type-II magnitude response is given by:
-
(3)
-
Where is the filter order, is the cut-off frequency, and is the attenuation factor with stop-band attenuation in dB. The poles are the roots of:
-
(4)
-
And the zeros are given by:
-
(5)
-
For . The characteristics of the Chebyshev Type-II filter are shown in Figs. 1-4.