Difference between revisions of "CoE 197U Scaling"
| (31 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
== Moore's Law == | == Moore's Law == | ||
| − | In 1965, [https://en.wikipedia.org/wiki/Gordon_Moore Gordon Moore] published a 4-page paper entitled | + | In 1965, [https://en.wikipedia.org/wiki/Gordon_Moore Gordon Moore] published a 4-page paper entitled ''Cramming more components onto integrated circuits''<ref name="moore1965">Gordon E Moore, Cramming more components onto integrated circuits, ''Electronics'', Volume 38, Number 8, April 19, 1965 ([https://newsroom.intel.com/wp-content/uploads/sites/11/2018/05/moores-law-electronics.pdf pdf])</ref>, where he predicted that the number of components in an integrated circuit will increase by a factor of two every year, as shown in Fig. 1. Note that he based his extrapolation on just 4 data points! |
{| | {| | ||
|[[File:Moore paper figure.png|thumb|350px|Figure 1: Gordon Moore's 1965 prediction<ref name="moore1965"/>.]] | |[[File:Moore paper figure.png|thumb|350px|Figure 1: Gordon Moore's 1965 prediction<ref name="moore1965"/>.]] | ||
| + | |[[File:Gordon moore video.jpg|thumb|350px|link=https://www.youtube.com/watch?v=ylgk3HEyZ_g|[https://www.youtube.com/watch?v=ylgk3HEyZ_g Gordon Moore: Thoughts on the 50th Anniversary of Moore’s Law]]] | ||
|- | |- | ||
|} | |} | ||
| Line 17: | Line 18: | ||
|} | |} | ||
| − | For more than 30 years, the development of integrated circuits continued roughly on the trajectory predicted by Moore's Law. This steady advance has relied heavily on the advances in device and fabrication technologies. Device dimensions are gone down by a factor of approximately 0.7 every generation, giving us approximately a 50% reduction in device area every 2 years, as seen in Fig. 3. | + | == Challenges in Digital Design == |
| + | [[File:Feature size scaling.png|thumb|430px|Figure 3: Technology node and transistor gate length versus calendar year<ref name="thompson2006">S. E. Thompson, S. Parthasarathy, | ||
| + | Moore's law: the future of Si microelectronics, ''Materials Today'', Volume 9, Issue 6, 2006, Pages 20-25. ([https://doi.org/10.1016/S1369-7021(06)71539-5 link])</ref>.]] | ||
| + | |||
| + | For more than 30 years, the development of integrated circuits continued roughly on the trajectory predicted by Moore's Law. This steady advance has relied heavily on the advances in device and fabrication technologies. Device dimensions are gone down by a factor of approximately 0.7 every generation, giving us approximately a 50% reduction in device area every 2 years, as seen in Fig. 3. However, in the past decade, we have seen a slowdown in the pace of development and performance of integrated circuits, seen in Fig. 4, as we face various physical and manufacturing limitations. | ||
| + | |||
| + | === The Power Wall === | ||
| + | As MOS device sizes continue to scale, digital gate delays also decrease, leading to higher maximum operating frequencies. This results in higher average dynamic power consumption, <math>P_\mathrm{ave}</math>, which is proportional to the frequency of operation and the square of the supply voltage, or equivalently: | ||
| + | |||
| + | {{NumBlk|::|<math>P_\mathrm{ave}\propto V_{DD}^2\cdot f</math>|{{EquationRef|1}}}} | ||
| + | |||
| + | This gives rise to higher power densities or power per unit volume. Since the power is dissipated as heat, adequate cooling mechanisms must be put in place to prevent the temperature from rising to levels that can reduce the performance or cause permanent damage to the IC. In most applications, the additional cooling costs might not be worth the extra performance. Thus, instead of a steady increase as predicted by Moore's Law, clock frequencies are starting to level off, as seen in Fig. 4. As expected, the power and single-core performance also levels off. | ||
| − | + | From Eq. 1, we can see that we can also reduce the average dynamic power by reducing the supply voltage. The maximum supply voltage however, is determined by the thickness of the gate-oxide layer, <math>t_\mathrm{ox}</math>. Since the vertical transistor dimensions, including <math>t_\mathrm{ox}</math>, are scaled with the horizontal dimensions, in deeply scaled devices, the gate-oxide layer can only be several atomic layers thick. This then results in large gate electric fields that could exceed the dielectric breakdown voltage of the gate-oxideregion. This reduction of supply voltage to accommodate the process technology is shown in Fig. 5. | |
{| | {| | ||
| − | |||
| − | |||
|[[File:42-years-processor-trend.png|thumb|500px|Figure 4: Scaling and processor performance<ref name=rupp2018>K. Rupp, ''42 Years of Microprocessor Trend Data'', [https://www.karlrupp.net/2018/02/42-years-of-microprocessor-trend-data/ link]</ref>.]] | |[[File:42-years-processor-trend.png|thumb|500px|Figure 4: Scaling and processor performance<ref name=rupp2018>K. Rupp, ''42 Years of Microprocessor Trend Data'', [https://www.karlrupp.net/2018/02/42-years-of-microprocessor-trend-data/ link]</ref>.]] | ||
| + | |[[File:Power and vdd scaling.png|thumb|480px|Figure 5: Supply voltage and power scaling<ref name="kunert2015">B. Kunert, Integration and Application of Epitaxial Systems: III/V on Silicon for Optoelectronics, IMEC Belgium 2015 ([https://pulse-school.sciencesconf.org/conference/pulse-school/pages/Kunert_2015_PulseSchool_Bernardette_Kunert.pdf link])</ref>.]] | ||
|- | |- | ||
|} | |} | ||
| − | == | + | === Leakage Current === |
| + | [[File:Power density reduction.png|thumb|400px|Figure 6: Semiconductor power density<ref name="chen2007">Chen (IBM), ISS Europe 2007, ([https://www.sec.gov/Archives/edgar/data/937966/000115697307001753/u54325exv99w3.htm link]).</ref>.]] | ||
| + | In MOS transistors, the subthreshold current can be expressed as: | ||
| + | |||
| + | {{NumBlk|::|<math>I_D\propto \frac{W}{L}\cdot e^\frac{q\cdot \left(V_{GS}-V_{TH}\right)}{kT}</math>|{{EquationRef|2}}}} | ||
| + | |||
| + | Thus, even with <math>V_{GS}=0</math>, the drain current is not zero, but ideally this leakage current is very small compared to the MOS saturation current. The resulting leakage current also increases as the transistor lengths are reduced since the distance between the source and drain regions are also reduced. In deeply scaled technologies, the resulting static power consumed due to leakage current is projected to be comparable or even dominate the total chip power consumption, as shown in Fig. 7. This is problematic since the IC would consume a significant amount of power even when idle, losing one of the original advantages of CMOS over other technologies such as BJTs, shown in Fig. 6. | ||
| + | |||
| + | In digital CMOS gates, decreasing the supply voltage decreases the MOS saturation current, leading to increased delays, since: | ||
| + | |||
| + | {{NumBlk|::|<math>t_\mathrm{delay}\propto \frac{C_\mathrm{load}\cdot V_{DD}}{I_D} \propto \frac{C_\mathrm{load}\cdot V_{DD}}{\left(V_{DD} - V_{TH}\right)^2}</math>|{{EquationRef|3}}}} | ||
| + | |||
| + | One way to maintain performance is to reduce the MOS threshold voltage, <math>V_{TH}</math> as the supply voltage is reduced. However, lowering the threshold voltage increases the MOS subthreshold leakage current. This power-delay tradeoff prevents the supply and threshold voltages from scaling at the same rate as the device sizes, as seen in Fig. 8. | ||
{| | {| | ||
| − | + | |[[File:Leakage power.png|thumb|500px|Figure 7: Active and Leakage Power<ref name="haensch2006">W. Haensch et al., Silicon CMOS devices beyond scaling, ''IBM Journal of Research and Development'', vol. 50, no. 4.5, pp. 339-361, July 2006, doi: 10.1147/rd.504.0339.</ref>.]] | |
| − | |[[File:Leakage power.png|thumb|500px|Figure | + | |[[File:Vdd scaling itrs2004.png|thumb|400px|Figure 8: Supply and threshold voltage scaling<ref name="itrs2004">ITRS, ''The International Technology Roadmap for Semiconductors (2004 edition)'', 2004. Technical Report, http://public.itrs.net</ref>.]] |
|- | |- | ||
|} | |} | ||
| − | + | === Process Variations === | |
| − | + | Errors due to the limitations of the fabrication process can introduce systematic and random parameter variability in advanced CMOS circuits. For example, using photolithography to create nanometer-scale features smaller than the wavelength of light used, as seen in Fig. 9, has been compared to trying to paint a 1-mm line with a 1-inch paint brush, resulting in line-edge roughness. Another example is the increased warping in wafers with larger diameters, where significant deviations in doping and layer thickness can potentially occur at the edges of the wafer. | |
| − | + | ||
| − | + | These variations can manifest as power or delay variations as shown in Fig. 10. These variations can cause problems in circuits that are required to adhere to certain standards, e.g. WiFi, PCI, etc., where the speed has to conform to the specifications outlined in the standard. In battery operated devices, these variations in leakage or standby power can reduce battery life. | |
{| | {| | ||
| − | |[[File:Freq leak pvt.png|thumb|500px|Figure | + | |[[File:Lithography gap.png|thumb|400px|Figure 9: The lithography gap<ref name="sole2012">M. Sole, Layout Regularity for Design and Manufacturability, Universitat Politecnica de Catalunya, Barcelona, 2012 ([https://core.ac.uk/download/pdf/81575636.pdf link]).</ref>.]] |
| + | |[[File:Freq leak pvt.png|thumb|500px|Figure 10: Leakage and frequency variations<ref name="borkar2003">S. Borkar, T. Karnik, S. Narendra, J. Tschanz, A. Keshavarzi and V. De, Parameter variations and impact on circuits and microarchitecture, ''Proceedings 2003. Design Automation Conference'' (IEEE Cat. No.03CH37451), Anaheim, CA, USA, 2003, pp. 338-342, doi: 10.1145/775832.775920.</ref>.]] | ||
|- | |- | ||
|} | |} | ||
== Why Scale? == | == Why Scale? == | ||
| + | The motivation for scaling is centered around cost and performance, enabling us to perform tasks that were previously not possible, or if it were possible before, the cost was very prohibitive. Thus, the semiconductor industry continues to invest in technologies that would continue the scaling of integrated circuits for as long as possible. Fig. 11 shows a possible trajectory of how scaling supports the computing industry in the artificial intelligence field. | ||
{| | {| | ||
| − | + | |[[File:Calculations vs year.png|thumb|900px|Figure 11: Calculations per second for a fixed cost<ref name="bcaresearch">BCA Research ([https://www.bcaresearch.com/images/Peter_PPT_presentation%2013.pdf link]).</ref>.]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |[[File:Calculations vs year.png|thumb|900px|Figure | ||
|- | |- | ||
|} | |} | ||
== The Cost of Integrated Circuits == | == The Cost of Integrated Circuits == | ||
| − | [[File:Wafer and die.png|thumb|500px|Figure | + | [[File:Wafer and die.png|thumb|500px|Figure 12: A wafer showing the individual die<ref name="dennis2013">J. Dennis, CMOS Compatible Bulk Micromachining, IntechOpen 2013 ([https://www.intechopen.com/books/advances-in-micro-nano-electromechanical-systems-and-fabrication-technologies/cmos-compatible-bulk-micromachining link])</ref>.]] |
Cost is the main motivation for reducing device sizes. Aside from the marked improvement in speed, more transistors can be integrated in the same die or wafer, and this results in the significant reduction in the cost per transistor. The total cost of producing an integrated circuit can be broken down into two components: (1) the fixed or non-recurrent engineering costs (NRE), and (2) the variable or recurrent costs. | Cost is the main motivation for reducing device sizes. Aside from the marked improvement in speed, more transistors can be integrated in the same die or wafer, and this results in the significant reduction in the cost per transistor. The total cost of producing an integrated circuit can be broken down into two components: (1) the fixed or non-recurrent engineering costs (NRE), and (2) the variable or recurrent costs. | ||
| Line 74: | Line 94: | ||
Thus, the cost of an integrated circuit can be expressed as: | Thus, the cost of an integrated circuit can be expressed as: | ||
| − | {{NumBlk|::|<math>\mathrm{cost\,per\,IC} = \mathrm{variable\,cost\,per\,IC} + \frac{\mathrm{fixed\,cost}}{\mathrm{volume}}</math>|{{EquationRef| | + | {{NumBlk|::|<math>\mathrm{cost\,per\,IC} = \mathrm{variable\,cost\,per\,IC} + \frac{\mathrm{fixed\,cost}}{\mathrm{volume}}</math>|{{EquationRef|4}}}} |
Where the components of the variable cost are: | Where the components of the variable cost are: | ||
| − | {{NumBlk|::|<math>\mathrm{variable\,cost\,per\,IC} = \frac{\mathrm{die\,cost} + \mathrm{die\,test\,cost} + \mathrm{die\,packaging\,cost}}{\mathrm{final\,test\,yield}}</math>|{{EquationRef| | + | {{NumBlk|::|<math>\mathrm{variable\,cost\,per\,IC} = \frac{\mathrm{die\,cost} + \mathrm{die\,test\,cost} + \mathrm{die\,packaging\,cost}}{\mathrm{final\,test\,yield}}</math>|{{EquationRef|5}}}} |
=== Die Cost === | === Die Cost === | ||
| − | The cost of a die or chip is dependent on the (1) cost of a wafer, shown in Fig. | + | The cost of a die or chip is dependent on the (1) cost of a wafer, shown in Fig. 12, (2) the number of chips or dies in a wafer, and (3) the die yield: |
| − | {{NumBlk|::|<math>\mathrm{die\,cost} = \frac{\mathrm{wafer\,cost}}{\mathrm{dies\,per\,wafer}\times\mathrm{die\,yield}}</math>|{{EquationRef| | + | {{NumBlk|::|<math>\mathrm{die\,cost} = \frac{\mathrm{wafer\,cost}}{\mathrm{dies\,per\,wafer}\times\mathrm{die\,yield}}</math>|{{EquationRef|6}}}} |
| − | Note that increasing the number of dies in a wafer can reduce the cost per die. This can be done by increasing the size of the wafer, as long as the increase in cost due to the larger wafer size is offset by the reduction in overall cost due to more dies in a wafer, as seen in Fig. | + | Note that increasing the number of dies in a wafer can reduce the cost per die. This can be done by increasing the size of the wafer, as long as the increase in cost due to the larger wafer size is offset by the reduction in overall cost due to more dies in a wafer, as seen in Fig. 13. However, increasing the wafer size can cause structural problems such as warping of the wafer, leading to increased device variability. One way to solve this problem is to increase the thickness of the wafer, as shown in Fig. 14. |
{| | {| | ||
| − | |[[File:Wafer size.gif|thumb|500px|Figure | + | |[[File:Wafer size.gif|thumb|500px|Figure 13: The evolution of wafer size<ref name="stallhofer2011">P. Stallhofer, Why Are Silicon Wafers as Thick as They Are? In: Burghartz J. (eds) ''Ultra-thin Chip Technology and Applications'', Springer 2011, New York, NY. ([https://link.springer.com/chapter/10.1007/978-1-4419-7276-7_1 link])</ref>.]] |
| − | |[[File:Wafer thickness.gif|thumb|500px|Figure | + | |[[File:Wafer thickness.gif|thumb|500px|Figure 14: Wafer thickness<ref name="stallhofer2011"></ref>.]] |
|- | |- | ||
|} | |} | ||
| Line 96: | Line 116: | ||
The yield, <math>Y</math>, is defined as the ratio of good dies in a wafer relative to the total number of dies in a wafer, or equivalently in percent units: | The yield, <math>Y</math>, is defined as the ratio of good dies in a wafer relative to the total number of dies in a wafer, or equivalently in percent units: | ||
| − | {{NumBlk|::|<math>Y = \frac{\mathrm{number\,of\,good\,dies\,per\,wafer}}{\mathrm{total\,number\,of\,dies\,per\,wafer}}\times 100\%</math>|{{EquationRef| | + | {{NumBlk|::|<math>Y = \frac{\mathrm{number\,of\,good\,dies\,per\,wafer}}{\mathrm{total\,number\,of\,dies\,per\,wafer}}\times 100\%</math>|{{EquationRef|7}}}} |
We can estimate the total number of dies, each with area <math>A_\mathrm{die}</math>, in a wafer with diameter, <math>d</math> as: | We can estimate the total number of dies, each with area <math>A_\mathrm{die}</math>, in a wafer with diameter, <math>d</math> as: | ||
| − | {{NumBlk|::|<math>\mathrm{total\,number\,of\,dies\,per\,wafer} = \frac{\pi \cdot \left(\frac{d}{2}\right)^2}{A_\mathrm{die}} - \frac{\pi \cdot d}{\sqrt{2\cdot A_\mathrm{die}}}</math>|{{EquationRef| | + | {{NumBlk|::|<math>\mathrm{total\,number\,of\,dies\,per\,wafer} = \frac{\pi \cdot \left(\frac{d}{2}\right)^2}{A_\mathrm{die}} - \frac{\pi \cdot d}{\sqrt{2\cdot A_\mathrm{die}}}</math>|{{EquationRef|8}}}} |
| − | The first term in Eq. | + | The first term in Eq. 8 gives us the total wafer area divided by the die area. However, as seen in Fig. 15, there are partial dies at the edge of the wafer that must be discounted since they cannot be used. The number of partial dies at the edge is estimated by the second term in Eq. 5. Note that by reducing the die area, the yield can significantly increase for the same wafer defect pattern, as shown in Fig. 16. Thus, for large die sizes, the die cost is higher since the yield is lower, thus the cost of the good dies must shoulder the cost of the bad dies. |
{| | {| | ||
| − | |[[File:360mm2 wafer yield 0.05pcm2.svg|thumb|450px|Figure | + | |[[File:360mm2 wafer yield 0.05pcm2.svg|thumb|450px|Figure 15: Wafer defects due to fabrication non-idealities<ref name="wikichip_yield">WikiChip ([https://en.wikichip.org/wiki/yield link])</ref>.]] |
| − | |[[File:Yield die size.png|thumb|450px|Figure | + | |[[File:Yield die size.png|thumb|450px|Figure 16: The effect of die size on yield<ref name="choi2016">K. Choi's lecture notes on Design Metrics, CMPEN 411: VLSI Digital Circuits, Pennsylvania State University, Fall 2016 ([http://www.cse.psu.edu/~kxc104/class/cmpen411/14f/lec/C411L02DMetrics.pdf link])</ref>.]] |
|- | |- | ||
|} | |} | ||
| + | |||
| + | {{Note|[[CoE197U-A1.1 | '''Activity A1.1''' IC Fabrication and Scaling]] -- This activity provides an overview of the CMOS fabrication process, and its future directions.|reminder}} | ||
== References == | == References == | ||
<references /> | <references /> | ||
Latest revision as of 15:03, 1 March 2021
Contents
Moore's Law
In 1965, Gordon Moore published a 4-page paper entitled Cramming more components onto integrated circuits[1], where he predicted that the number of components in an integrated circuit will increase by a factor of two every year, as shown in Fig. 1. Note that he based his extrapolation on just 4 data points!
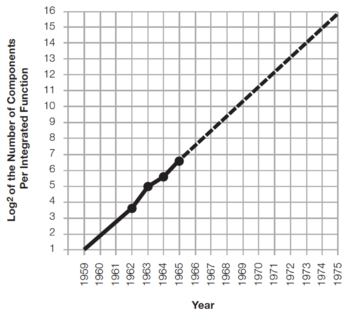 Figure 1: Gordon Moore's 1965 prediction[1]. |
Why is this paper and the graph in Fig. 1 important? Gordon Moore's prediction, also known as Moore's Law, has reflected and, more importantly, driven the steady and rapid progress in computing technology[2]. Thus, satisfying Moore's Law has become the goal instead of being merely a prediction.
Evolution of Complexity
As Gordon Moore predicted, the cost and performance advantage of putting more and more devices into a single integrated circuit (IC) led to the rapid increase in circuit complexity. One convenient indicator of circuit complexity is the number of transistors contained in a single IC, reaching the 1-billion transistor level in 2010, and achieving almost 50 billion transistors in 2020, as shown in Fig. 2.
 Figure 2: Transistor Count (1970 - 2020)[3]. |
Challenges in Digital Design
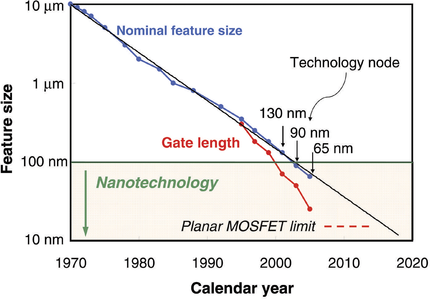
For more than 30 years, the development of integrated circuits continued roughly on the trajectory predicted by Moore's Law. This steady advance has relied heavily on the advances in device and fabrication technologies. Device dimensions are gone down by a factor of approximately 0.7 every generation, giving us approximately a 50% reduction in device area every 2 years, as seen in Fig. 3. However, in the past decade, we have seen a slowdown in the pace of development and performance of integrated circuits, seen in Fig. 4, as we face various physical and manufacturing limitations.
The Power Wall
As MOS device sizes continue to scale, digital gate delays also decrease, leading to higher maximum operating frequencies. This results in higher average dynamic power consumption, , which is proportional to the frequency of operation and the square of the supply voltage, or equivalently:
-
(1)
-
This gives rise to higher power densities or power per unit volume. Since the power is dissipated as heat, adequate cooling mechanisms must be put in place to prevent the temperature from rising to levels that can reduce the performance or cause permanent damage to the IC. In most applications, the additional cooling costs might not be worth the extra performance. Thus, instead of a steady increase as predicted by Moore's Law, clock frequencies are starting to level off, as seen in Fig. 4. As expected, the power and single-core performance also levels off.
From Eq. 1, we can see that we can also reduce the average dynamic power by reducing the supply voltage. The maximum supply voltage however, is determined by the thickness of the gate-oxide layer, . Since the vertical transistor dimensions, including , are scaled with the horizontal dimensions, in deeply scaled devices, the gate-oxide layer can only be several atomic layers thick. This then results in large gate electric fields that could exceed the dielectric breakdown voltage of the gate-oxideregion. This reduction of supply voltage to accommodate the process technology is shown in Fig. 5.
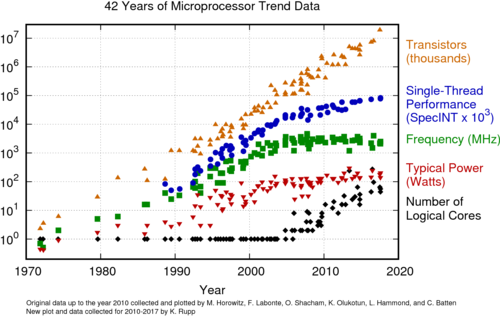 Figure 4: Scaling and processor performance[5]. |
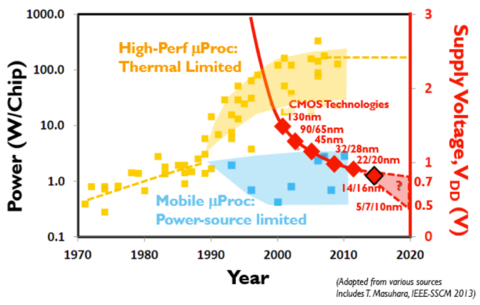 Figure 5: Supply voltage and power scaling[6]. |
Leakage Current
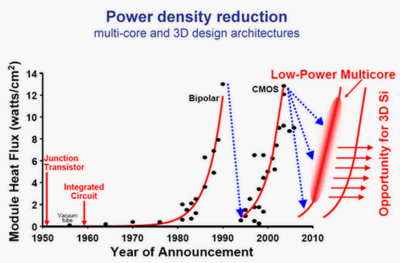
In MOS transistors, the subthreshold current can be expressed as:
-
(2)
-
Thus, even with , the drain current is not zero, but ideally this leakage current is very small compared to the MOS saturation current. The resulting leakage current also increases as the transistor lengths are reduced since the distance between the source and drain regions are also reduced. In deeply scaled technologies, the resulting static power consumed due to leakage current is projected to be comparable or even dominate the total chip power consumption, as shown in Fig. 7. This is problematic since the IC would consume a significant amount of power even when idle, losing one of the original advantages of CMOS over other technologies such as BJTs, shown in Fig. 6.
In digital CMOS gates, decreasing the supply voltage decreases the MOS saturation current, leading to increased delays, since:
-
(3)
-
One way to maintain performance is to reduce the MOS threshold voltage, as the supply voltage is reduced. However, lowering the threshold voltage increases the MOS subthreshold leakage current. This power-delay tradeoff prevents the supply and threshold voltages from scaling at the same rate as the device sizes, as seen in Fig. 8.
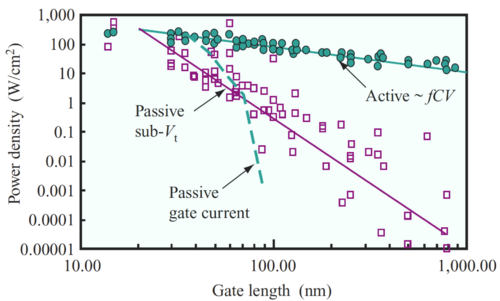 Figure 7: Active and Leakage Power[8]. |
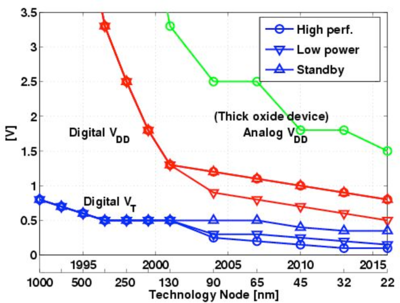 Figure 8: Supply and threshold voltage scaling[9]. |
Process Variations
Errors due to the limitations of the fabrication process can introduce systematic and random parameter variability in advanced CMOS circuits. For example, using photolithography to create nanometer-scale features smaller than the wavelength of light used, as seen in Fig. 9, has been compared to trying to paint a 1-mm line with a 1-inch paint brush, resulting in line-edge roughness. Another example is the increased warping in wafers with larger diameters, where significant deviations in doping and layer thickness can potentially occur at the edges of the wafer.
These variations can manifest as power or delay variations as shown in Fig. 10. These variations can cause problems in circuits that are required to adhere to certain standards, e.g. WiFi, PCI, etc., where the speed has to conform to the specifications outlined in the standard. In battery operated devices, these variations in leakage or standby power can reduce battery life.
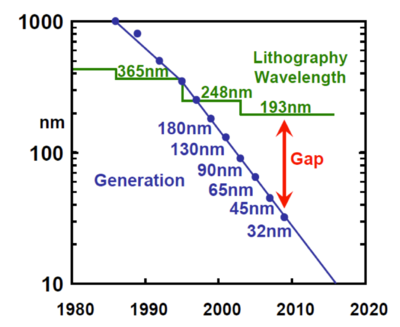 Figure 9: The lithography gap[10]. |
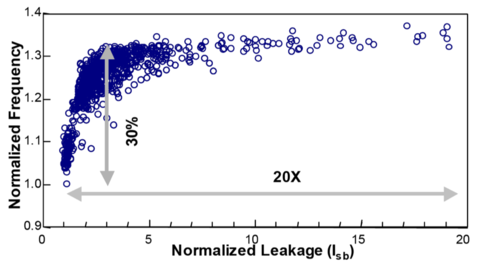 Figure 10: Leakage and frequency variations[11]. |
Why Scale?
The motivation for scaling is centered around cost and performance, enabling us to perform tasks that were previously not possible, or if it were possible before, the cost was very prohibitive. Thus, the semiconductor industry continues to invest in technologies that would continue the scaling of integrated circuits for as long as possible. Fig. 11 shows a possible trajectory of how scaling supports the computing industry in the artificial intelligence field.
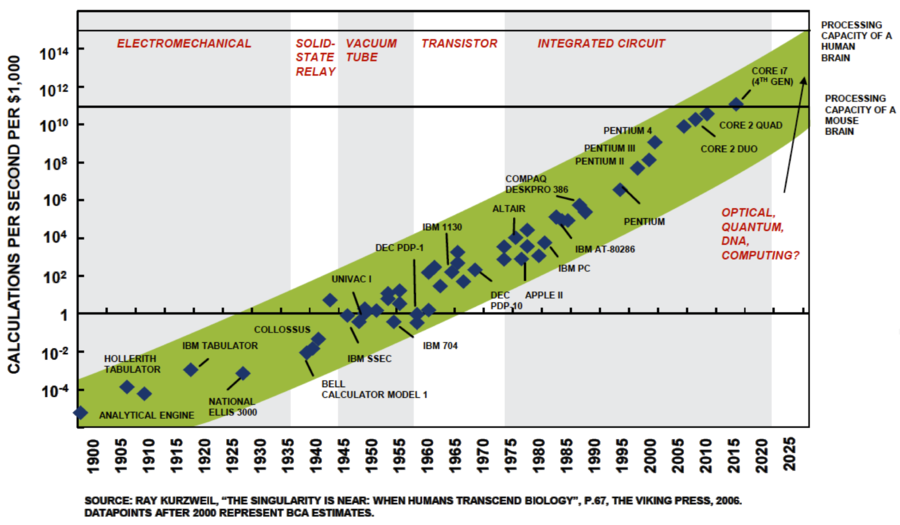 Figure 11: Calculations per second for a fixed cost[12]. |
The Cost of Integrated Circuits
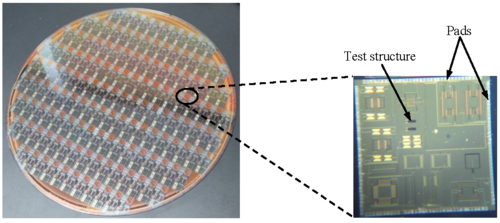
Cost is the main motivation for reducing device sizes. Aside from the marked improvement in speed, more transistors can be integrated in the same die or wafer, and this results in the significant reduction in the cost per transistor. The total cost of producing an integrated circuit can be broken down into two components: (1) the fixed or non-recurrent engineering costs (NRE), and (2) the variable or recurrent costs.
- Non-Recurrent Engineering (NRE) Costs
-
- NRE costs are overhead costs independent of volume, i.e. the number of integrated circuits made or sold.
- Examples of NRE costs include design time and manpower, CAD tools and equipment, mask generation costs, etc.
- Recurrent Costs
-
- Costs that are proportional to the volume of ICs produced.
- This includes the fabrication costs, packaging costs, and testing costs.
- In most cases, these costs are proportional the chip area.
Thus, the cost of an integrated circuit can be expressed as:
-
(4)
-
Where the components of the variable cost are:
-
(5)
-
Die Cost
The cost of a die or chip is dependent on the (1) cost of a wafer, shown in Fig. 12, (2) the number of chips or dies in a wafer, and (3) the die yield:
-
(6)
-
Note that increasing the number of dies in a wafer can reduce the cost per die. This can be done by increasing the size of the wafer, as long as the increase in cost due to the larger wafer size is offset by the reduction in overall cost due to more dies in a wafer, as seen in Fig. 13. However, increasing the wafer size can cause structural problems such as warping of the wafer, leading to increased device variability. One way to solve this problem is to increase the thickness of the wafer, as shown in Fig. 14.
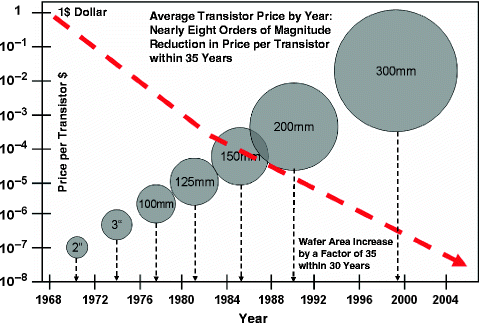 Figure 13: The evolution of wafer size[14]. |
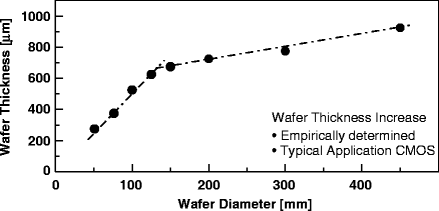 Figure 14: Wafer thickness[14]. |
Yield
The yield, , is defined as the ratio of good dies in a wafer relative to the total number of dies in a wafer, or equivalently in percent units:
-
(7)
-
We can estimate the total number of dies, each with area , in a wafer with diameter, as:
-
(8)
-
The first term in Eq. 8 gives us the total wafer area divided by the die area. However, as seen in Fig. 15, there are partial dies at the edge of the wafer that must be discounted since they cannot be used. The number of partial dies at the edge is estimated by the second term in Eq. 5. Note that by reducing the die area, the yield can significantly increase for the same wafer defect pattern, as shown in Fig. 16. Thus, for large die sizes, the die cost is higher since the yield is lower, thus the cost of the good dies must shoulder the cost of the bad dies.
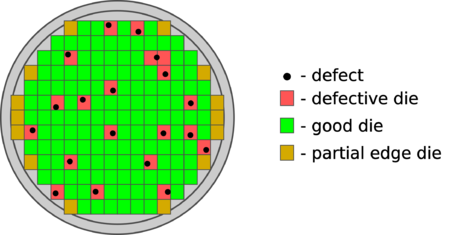 Figure 15: Wafer defects due to fabrication non-idealities[15]. |
 Figure 16: The effect of die size on yield[16]. |
References
- ↑ Jump up to: 1.0 1.1 Gordon E Moore, Cramming more components onto integrated circuits, Electronics, Volume 38, Number 8, April 19, 1965 (pdf)
- ↑ Gordon Moore: The Man Whose Name Means Progress, IEEE Spectrum, March 2015.
- ↑ Wikimedia
- ↑ S. E. Thompson, S. Parthasarathy, Moore's law: the future of Si microelectronics, Materials Today, Volume 9, Issue 6, 2006, Pages 20-25. (link)
- ↑ K. Rupp, 42 Years of Microprocessor Trend Data, link
- ↑ B. Kunert, Integration and Application of Epitaxial Systems: III/V on Silicon for Optoelectronics, IMEC Belgium 2015 (link)
- ↑ Chen (IBM), ISS Europe 2007, (link).
- ↑ W. Haensch et al., Silicon CMOS devices beyond scaling, IBM Journal of Research and Development, vol. 50, no. 4.5, pp. 339-361, July 2006, doi: 10.1147/rd.504.0339.
- ↑ ITRS, The International Technology Roadmap for Semiconductors (2004 edition), 2004. Technical Report, http://public.itrs.net
- ↑ M. Sole, Layout Regularity for Design and Manufacturability, Universitat Politecnica de Catalunya, Barcelona, 2012 (link).
- ↑ S. Borkar, T. Karnik, S. Narendra, J. Tschanz, A. Keshavarzi and V. De, Parameter variations and impact on circuits and microarchitecture, Proceedings 2003. Design Automation Conference (IEEE Cat. No.03CH37451), Anaheim, CA, USA, 2003, pp. 338-342, doi: 10.1145/775832.775920.
- ↑ BCA Research (link).
- ↑ J. Dennis, CMOS Compatible Bulk Micromachining, IntechOpen 2013 (link)
- ↑ Jump up to: 14.0 14.1 P. Stallhofer, Why Are Silicon Wafers as Thick as They Are? In: Burghartz J. (eds) Ultra-thin Chip Technology and Applications, Springer 2011, New York, NY. (link)
- ↑ WikiChip (link)
- ↑ K. Choi's lecture notes on Design Metrics, CMPEN 411: VLSI Digital Circuits, Pennsylvania State University, Fall 2016 (link)















