Difference between revisions of "EEE 51 Transistor Models"
| (21 intermediate revisions by the same user not shown) | |||
| Line 12: | Line 12: | ||
==== The BJT Transfer Characteristic ==== | ==== The BJT Transfer Characteristic ==== | ||
| + | <figure id="fig:BJT-CE-config"> | ||
[[File:Common-emitter_config.png|thumb|right|250px|Figure 1: The BJT common-emitter configuration.]] | [[File:Common-emitter_config.png|thumb|right|250px|Figure 1: The BJT common-emitter configuration.]] | ||
| − | The BJT common-emitter (CE) configuration is shown in | + | </figure> |
| + | The BJT common-emitter (CE) configuration is shown in <xr id="fig:BJT-CE-config"/>. We define the “input” signal as the base-emitter voltage, <math>V_{BE}</math>, and the “output” signal as the collector current <math>I_{C}</math>. Therefore, we can model the the BJT transfer characteristic using | ||
{{NumBlk|:|<math>I_{C}=I_{S}\cdot\left(e^{\frac{V_{BE}}{n\cdot V_{T}}}-1\right)\cdot\left(1+\frac{V_{CE}}{\left|V_{A}\right|}\right)</math>|{{EquationRef|1}}}} | {{NumBlk|:|<math>I_{C}=I_{S}\cdot\left(e^{\frac{V_{BE}}{n\cdot V_{T}}}-1\right)\cdot\left(1+\frac{V_{CE}}{\left|V_{A}\right|}\right)</math>|{{EquationRef|1}}}} | ||
| Line 21: | Line 23: | ||
{{NumBlk|:|<math>I_{C}\approx I_{S}\cdot e^{\frac{V_{BE}}{n\cdot V_{T}}}</math>|{{EquationRef|2}}}} | {{NumBlk|:|<math>I_{C}\approx I_{S}\cdot e^{\frac{V_{BE}}{n\cdot V_{T}}}</math>|{{EquationRef|2}}}} | ||
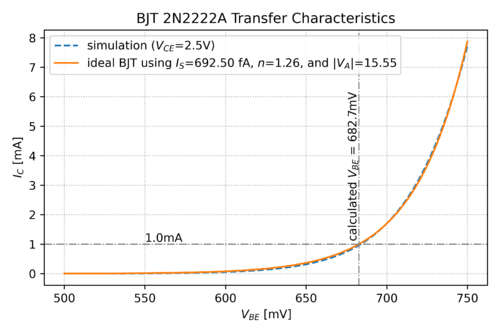
| − | Eq. ({{EquationNote|1}}), shown in | + | Eq. ({{EquationNote|1}}), shown in <xr id="fig:BJT-CE-transfer-char"/>, and superimposed with the transfer characteristic of the 2N2222A<ref>The 2N2222A [http://web.mit.edu/6.101/www/reference/2N2222A.pdf datasheet]</ref> NPN BJT, allows us to approximate the behavior of the “output” signal, in this case the collector current, when we change the base-emitter voltage, our “input” signal. |
| + | <figure id="fig:BJT-CE-transfer-char"> | ||
[[File:2N2222A_transfer_2500mV.png|thumb|center|500px|Figure 2: The BJT transfer characteristics of a 2N2222A NPN transistor.]] | [[File:2N2222A_transfer_2500mV.png|thumb|center|500px|Figure 2: The BJT transfer characteristics of a 2N2222A NPN transistor.]] | ||
| + | </figure> | ||
==== The MOSFET Transfer Characteristic ==== | ==== The MOSFET Transfer Characteristic ==== | ||
| Line 61: | Line 65: | ||
Consider an NPN BJT, in the forward-active region, that is biased with a DC base-emitter voltage of <math>V_{BE,Q}</math>. This would result in a DC collector current <math>I_{C,Q}</math>, and from Eq. ({{EquationNote|2}}), is equal to | Consider an NPN BJT, in the forward-active region, that is biased with a DC base-emitter voltage of <math>V_{BE,Q}</math>. This would result in a DC collector current <math>I_{C,Q}</math>, and from Eq. ({{EquationNote|2}}), is equal to | ||
| − | {{NumBlk|:|<math>I_{C,Q}=I_{S}\cdot e^{\frac{V_{BE,Q}}{V_{T}}}</math>|{{EquationRef|5}}}} | + | {{NumBlk|:|<math>I_{C,Q}=I_{S}\cdot e^{\frac{V_{BE,Q}}{n\cdot V_{T}}}</math>|{{EquationRef|5}}}} |
Note that we use the subscript Q to indicate that this is the quiescent <ref group=fn>Synonymous to an idle, or rest state.</ref> point DC bias, meaning that this is the purely DC voltage and current of the BJT when there are no disturbances present. | Note that we use the subscript Q to indicate that this is the quiescent <ref group=fn>Synonymous to an idle, or rest state.</ref> point DC bias, meaning that this is the purely DC voltage and current of the BJT when there are no disturbances present. | ||
| Line 71: | Line 75: | ||
Assuming that <math>v_{be}</math> is small enough that the transistor does not change its operating region, the collector current then becomes | Assuming that <math>v_{be}</math> is small enough that the transistor does not change its operating region, the collector current then becomes | ||
| − | {{NumBlk|:|<math>i_{C}=I_{C,Q}+i_{c}=I_{S}\cdot e^{\frac{v_{BE}}{V_{T}}}=I_{S}\cdot e^{\frac{V_{BE,Q}+v_{be}}{V_{T}}}</math>|{{EquationRef|7}}}} | + | {{NumBlk|:|<math>i_{C}=I_{C,Q}+i_{c}=I_{S}\cdot e^{\frac{v_{BE}}{n\cdot V_{T}}}=I_{S}\cdot e^{\frac{V_{BE,Q}+v_{be}}{n\cdot V_{T}}}</math>|{{EquationRef|7}}}} |
where <math>i_{c}</math> is the collector current deviation away from its quiescent point, due to the addition of the “small” signal <math>v_{be}</math>. Simplifying Eq. ({{EquationNote|7}}), and using Eq. ({{EquationNote|5}}), we get | where <math>i_{c}</math> is the collector current deviation away from its quiescent point, due to the addition of the “small” signal <math>v_{be}</math>. Simplifying Eq. ({{EquationNote|7}}), and using Eq. ({{EquationNote|5}}), we get | ||
| − | {{NumBlk|:|<math>I_{C,Q}+i_{c}=I_{S}\cdot e^{\frac{V_{BE,Q}}{V_{T}}}\cdot e^{\frac{v_{be}}{V_{T}}}=I_{C,Q}\cdot e^{\frac{v_{be}}{V_{T}}}</math>|{{EquationRef|8}}}} | + | {{NumBlk|:|<math>I_{C,Q}+i_{c}=I_{S}\cdot e^{\frac{V_{BE,Q}}{n\cdot V_{T}}}\cdot e^{\frac{v_{be}}{n\cdot V_{T}}}=I_{C,Q}\cdot e^{\frac{v_{be}}{n\cdot V_{T}}}</math>|{{EquationRef|8}}}} |
As expected, <math>i_{c}</math> is a nonlinear function (exponential) of <math>v_{be}</math>. Now, let us try to linearize this relationship. Here we present two methods, but as we will see, they turn out to be equivalent. | As expected, <math>i_{c}</math> is a nonlinear function (exponential) of <math>v_{be}</math>. Now, let us try to linearize this relationship. Here we present two methods, but as we will see, they turn out to be equivalent. | ||
| Line 88: | Line 92: | ||
{{NumBlk|:|<math>e^{x}=e^{0}+\frac{e^{0}}{1!}x+\frac{e^{0}}{2!}x^{2}+\frac{e^{0}}{3!}x^{3}+\ldots=1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\ldots</math>|{{EquationRef|10}}}} | {{NumBlk|:|<math>e^{x}=e^{0}+\frac{e^{0}}{1!}x+\frac{e^{0}}{2!}x^{2}+\frac{e^{0}}{3!}x^{3}+\ldots=1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\ldots</math>|{{EquationRef|10}}}} | ||
| − | Thus, expanding <math>e^{\tfrac{v_{be}}{V_{T}}}</math>, we get | + | Thus, expanding <math>e^{\tfrac{v_{be}}{n\cdot V_{T}}}</math>, we get |
| − | {{NumBlk|:|<math>e^{\frac{v_{be}}{V_{T}}}=1+\frac{v_{be}}{V_{T}}+\frac{1}{2!}\left(\frac{v_{be}}{V_{T}}\right)^{2}+\frac{1}{3!}\left(\frac{v_{be}}{V_{T}}\right)^{3}+\ldots</math>|{{EquationRef|11}}}} | + | {{NumBlk|:|<math>e^{\frac{v_{be}}{n\cdot V_{T}}}=1+\frac{v_{be}}{n\cdot V_{T}}+\frac{1}{2!}\left(\frac{v_{be}}{n\cdot V_{T}}\right)^{2}+\frac{1}{3!}\left(\frac{v_{be}}{n\cdot V_{T}}\right)^{3}+\ldots</math>|{{EquationRef|11}}}} |
| − | Substituting Eq. [ | + | Substituting Eq. ({{EquationNote|11}}) into Eq. ({{EquationNote|8}}) gives us |
| + | |||
| + | {{NumBlk|:|<math>I_{C,Q}+i_{c}=I_{C,Q}+\frac{I_{C,Q}}{n\cdot V_{T}}v_{be}+\frac{1}{2!}I_{C,Q}\left(\frac{v_{be}}{n\cdot V_{T}}\right)^{2}+\frac{1}{3!}I_{C,Q}\left(\frac{v_{be}}{n\cdot V_{T}}\right)^{3}+\ldots</math>|{{EquationRef|12}}}} | ||
| + | |||
| + | We can remove the DC quiescent current term I_{C,Q} from both sides of Eq. ({{EquationNote|12}}), giving us | ||
| + | |||
| + | {{NumBlk|:|<math>i_{c}=\frac{I_{C,Q}}{n\cdot V_{T}}v_{be}+\frac{1}{2!}I_{C,Q}\left(\frac{v_{be}}{n\cdot V_{T}}\right)^{2}+\frac{1}{3!}I_{C,Q}\left(\frac{v_{be}}{n\cdot V_{T}}\right)^{3}+\ldots</math>|{{EquationRef|13}}}} | ||
| + | |||
| + | Eq. ({{EquationNote|13}}) is a very important result. First, it gives us an alternative to Eq. ({{EquationNote|8}}) in computing for <math>i_{c}</math>, but more importantly, it shows us that for <math>\tfrac{v_{be}}{n\cdot V_{T}}\ll1</math>, all the terms of Eq. ({{EquationNote|13}}) become very much less than the first term. Thus, we can approximate <math>i_{c}</math> as | ||
| + | |||
| + | {{NumBlk|:|<math>i_{c}\approx\frac{I_{C,Q}}{n\cdot V_{T}}\cdot v_{be}</math>|{{EquationRef|14}}}} | ||
| + | |||
| + | Note that Eq. ({{EquationNote|14}}) provides us with a “linear” relationship between <math>i_{c}</math> and <math>v_{be}</math>, and is a good approximation only when <math>v_{be}</math> is small enough, that is when <math>v_{be}\ll n\cdot V_{T}</math>. In this case, we can assume that <math>v_{be}</math> is a “small signal”. Eq. ({{EquationNote|13}}) also allows us to compute how much error we are incurring if we use Eq. ({{EquationNote|14}}), by summing up the remaining terms that we have ignored. Also, a very important observation here is that the relationship between <math>i_{c}</math> and <math>v_{be}</math> depends on DC quiescent current, <math>I_{C,Q}</math>. | ||
| + | |||
| + | ==== Method 2 ==== | ||
| + | Another approach to linearizing the relationship between <math>i_{c}</math> and <math>v_{be}</math> is by looking at this relationship graphically. Consider the graph of a BJT transfer characteristic shown in Fig. [fig:Linearization-of-the-bjt-transfer-char]. | ||
| + | |||
| + | If point <math>A</math> is the DC quiescent point, then <math>y=V_{BE,Q}</math>, and <math>v=I_{C,Q}</math>. Also, if <math>\left|v_{be}\right|=\left|z-x\right|</math>, then adding <math>v_{be}</math> on top of <math>V_{BE,Q}</math> would result in the collector current also changing by an <math>\left|i_{c}\right|=\left|w-u\right|</math>. We are using the absolute value signs to indicate that both <math>v_{be}</math> and <math>i_{c}</math> can take on negative values. That is, when <math>v_{be}=0</math>, the total base-emitter voltage is <math>v_{BE}=y=V_{BE,Q}</math>. When <math>v_{be}</math> is at its maximum value, <math>v_{BE}=z=V_{BE,Q}+v_{be,\max}</math>, and the transistor is operating at point <math>C</math>. When <math>v_{be}</math> is at its minimum (negative) value, <math>v_{BE}=x=V_{BE,Q}-\left|v_{be,\min}\right|</math>, corresponding to point <math>B</math>. | ||
| + | |||
| + | For clarity, a possible time domain view is given in Fig. [fig:Time-domain-view] for <math>v_{BE}\left(t\right)=V_{BE,Q}+v_{be}\left(t\right)</math> and <math>i_{C}\left(t\right)=I_{C,Q}+i_{c}\left(t\right)</math>. Note that for time <math>t<t_{1}</math> and <math>t>t_{2}</math>, <math>v_{be}\left(t\right)=0</math>, thus, <math>i_{c}\left(t\right)=0</math>, which means that the transistor is in its quiescent point, that is <math>v_{BE}\left(t\right)=V_{BE,Q}</math> and <math>i_{C}\left(t\right)=I_{C,Q}</math>. | ||
| + | |||
| + | We can approximate the relationship between <math>v_{be}</math> and <math>i_{c}</math> using a straight line (linear!) passing through points <math>B</math> and <math>C</math>. If we know the slope, <math>m</math>, of this line, we can estimate the magnitude <math>i_{c}</math> given <math>v_{be}</math> as <math>i_{c}=m\cdot v_{be}</math>. However, finding the slope of this line is not very straightforward, and as seen in Fig. [fig:Linearization-of-the-bjt-transfer-char], using the dashed line will result in errors for points between <math>B</math> and <math>C</math>. On the other hand, if <math>v_{be}</math> is small, or equivalently if <math>x\rightarrow y</math> and <math>z\rightarrow y</math>, then the error becomes smaller, and our linear approximation becomes more accurate. The slope of our linear approximation, if we make <math>v_{be}</math> approach zero, can be expressed as | ||
| + | |||
| + | {{NumBlk|:|<math>m=\lim_{v_{be}\rightarrow0}\frac{i_{C}\left(V_{BE,Q}+v_{be}\right)-i_{C}\left(V_{BE.Q}\right)}{V_{BE,Q}+v_{be}-V_{BE,Q}}</math>|{{EquationRef|15}}}} | ||
| + | |||
| + | Recall that for a function, <math>f\left(x\right)</math>, its derivative at a point <math>x=X_{0}</math> is given as | ||
| + | |||
| + | {{NumBlk|:|<math>\left.\frac{\partial f\left(x\right)}{\partial x}\right|_{x=X_{0}}=\lim_{\Delta x\rightarrow0}\frac{f\left(X_{0}+\Delta x\right)-f\left(X_{0}\right)}{\Delta x}</math>|{{EquationRef|16}}}} | ||
| + | |||
| + | Thus, for small values of <math>v_{be}</math>, we can approximate <math>i_{c}</math> as | ||
| + | |||
| + | {{NumBlk|:|<math>i_{c}=\left.\frac{\partial I_{C}}{\partial V_{BE}}\right|_{V_{BE}=V_{BE,Q}}\cdot v_{be}=g_{m}\cdot v_{be}</math>|{{EquationRef|17}}}} | ||
| + | |||
| + | where <math>g_{m}</math> is known as the device or transistor transconductance, since it relates small variations in the base-emitter voltage and collector current -- the parameters of the transistor transfer characteristic. The transistor transconductance is formally defined as | ||
| + | |||
| + | {{NumBlk|:|<math>g_{m}=\left.\frac{\partial I_{C}}{\partial V_{BE}}\right|_{V_{BE}=V_{BE,Q}}</math>|{{EquationRef|18}}}} | ||
| + | |||
| + | Note that <math>g_{m}</math> has units of Siemens (S)<ref group=fn><math>1\,\mathrm{S}=1\,\mathrm{\tfrac{1}{\Omega}}=1\,\mho</math></ref>, and is dependent on the quiescent point. Thus, a different <math>V_{BE,Q}</math> would result in a different <math>I_{C,Q}</math>, and hence a different <math>g_{m}</math>. | ||
| + | |||
| + | By plugging in Eq. [eq:bjt-simple-transfer] into Eq. [eq:gm-definition], we can calculate the value of the transconductance for a BJT as | ||
| + | |||
| + | {{NumBlk|:|<math>g_{m}=\left.\frac{\partial I_{C}}{\partial V_{BE}}\right|_{V_{BE}=V_{BE,Q}}=\left.\frac{\partial}{\partial V_{BE}}\left(I_{S}\cdot e^{\frac{V_{BE}}{n\cdot V_{T}}}\right)\right|_{V_{BE}=V_{BE,Q}}=\frac{1}{n\cdot V_{T}}\cdot I_{S}\cdot e^{\frac{V_{BE,Q}}{n\cdot V_{T}}}=\frac{I_{C,Q}}{n\cdot V_{T}}</math>|{{EquationRef|19}}}} | ||
| + | |||
| + | Thus, Eq. [eq:bjt-gm] makes Eq. [eq:gm-slope] equivalent to Eq. [eq:ic-linear1], which should not be that surprising since the Taylor Series coefficients are obtained using derivatives and we are only approximating the transfer characteristic by the first derivative term. | ||
| + | |||
| + | We have just covered a very important concept: linearizing the BJT transfer function allows us to approximate the relationship of <math>i_{c}</math> and <math>v_{be}</math> using a linear function, given by Eq. [eq:gm-slope], instead of using Eq. [eq:ic-eq+small-signal-2], an exponential equation. Also, if the signals we are dealing with are made smaller, then the errors we incur when using this linear approximation is reduced. | ||
| + | |||
| + | So far, we have used the BJT transfer characteristic. The process is exactly the same when dealing with MOSFETs. We can derive the Taylor Series expansion of Eq. [eq:mos-simple-transfer] by just expanding the quadratic term | ||
| + | |||
| + | {{NumBlk|:|<math>I_{D,Q}+i_{d}=k\cdot\left(V_{GS,Q}+v_{gs}-V_{TH}\right)^{2}=k\cdot\left(V_{GS,Q}-V_{TH}\right)^{2}+2k\cdot\left(V_{GS,Q}-V_{TH}\right)\cdot v_{gs}+k\cdot v_{gs}^{2}</math>|{{EquationRef|20}}}} | ||
| + | |||
| + | Since Eq. [eq:mos-simple-transfer] is already a polynomial, the Taylor Series representation shown in Eq. [eq:mos-expansion-transfer] is a finite series, and for our purposes, we group these terms into three. The first term in Eq. [eq:mos-expansion-transfer] is equal to <math>I_{D,Q}</math>. Therefore, we can write out the expression for <math>i_{d}</math> using the remaining two terms | ||
| + | |||
| + | {{NumBlk|:|<math>i_{d}=2k\cdot\left(V_{GS,Q}-V_{TH}\right)\cdot v_{gs}+k\cdot v_{gs}^{2}</math>|{{EquationRef|21}}}} | ||
| + | |||
| + | Again, if <math>v_{gs}</math> is small, then we can ignore the second term of Eq. [eq:mos-expansion-transfer-2], resulting in the linear relationship | ||
| + | |||
| + | {{NumBlk|:|<math>i_{d}=2k\cdot\left(V_{GS,Q}-V_{TH}\right)\cdot v_{gs}</math>|{{EquationRef|22}}}} | ||
| + | |||
| + | If we use the definition of transconductance given in Eq. [eq:gm-definition], and apply it to the MOSFET transfer characteristic given in Eq. [eq:mos-simple-transfer], we would get | ||
| + | |||
| + | {{NumBlk|:|<math>g_{m}=\left.\frac{\partial I_{D}}{\partial V_{GS}}\right|_{V_{GS}=V_{GS,Q}}=\left.\frac{\partial}{\partial V_{GS}}\left(k\cdot\left(V_{GS}-V_{TH}\right)^{2}\right)\right|_{V_{GS}=V_{GS,Q}}=2k\cdot\left(V_{GS,Q}-V_{TH}\right)</math>|{{EquationRef|23}}}} | ||
| + | |||
| + | Using Eqs. [eq:mos-simple-transfer] and [eq:mos-gm-defn], we can derive the other common forms of the MOSFET transconductance | ||
| + | |||
| + | {{NumBlk|:|<math>g_{m}=2k\cdot\left(V_{GS,Q}-V_{TH}\right)=\frac{2\cdot I_{D,Q}}{V_{GS,Q}-V_{TH}}=\sqrt{4k\cdot I_{D,Q}}</math>|{{EquationRef|24}}}} | ||
| + | |||
| + | Once again, we see that our two linearization methods are equivalent, thus | ||
| + | |||
| + | {{NumBlk|:|<math>i_{d}=g_{m}\cdot v_{gs}</math>|{{EquationRef|25}}}} | ||
| + | |||
| + | It is very important to remember that even though <math>g_{m}</math> is a function of the quiescent DC currents and voltages (<math>V_{BE,Q}</math> and <math>I_{C,Q}</math>, or <math>V_{GS,Q}</math> and <math>I_{D,Q}</math>), the linearized relationships using <math>g_{m}</math> in Eqs. [eq:gm-slope] and [eq:mos-linearized-2] only relates the small signal disturbances superimposed on the DC signals, <math>i_{c}</math> and <math>v_{be}</math>, or <math>i_{d}</math> and <math>v_{gs}</math>. Also, the linearization methods presented here are general techniques, independent of the transistor operating region, and can be applied to the large signal characteristic of any device that we may want to linearize. | ||
| + | |||
| + | === The Small-Signal Equivalent Circuit === | ||
== Notes == | == Notes == | ||
Latest revision as of 16:41, 23 June 2020
In EEE 41, you studied the fundamental concepts of how transistors can be realized using semiconductors, specifically, the two most popular transistors currently in use: the bipolar junction transistor (BJT) and the metal-oxide field-effect transistor (MOSFET).
In EEE 51, we want to be able to use these transistors (as well as other semiconductor devices such as diodes) to design and implement useful electronic circuits. This means we have to be able to describe, and eventually predict, the behavior of the terminal voltages and currents of these devices. We can accomplish this by using transistor models.
Large Signal Transistor Models
The large signal transistor models allow us to describe the electrical behavior of the transistor, when a voltage or current is varied over its allowable range. Here, we can see how varying the terminal voltages (and currents) determine the operating region of the transistor. Since there are many combinations of voltages and currents available for us to choose from, it is convenient to standardize which terminal voltages/currents we can use. This makes it easy to compare different transistors, as well as to systematically analyze and design electronic circuits based on these transistors.
The standard large signal transistor characteristics that we use are (1) the transfer characteristics, (2) the output characteristics, and (3) the input characteristics. Note that these models are normally considered as DC or low-frequency models, where we assume that the transistor parasitic capacitances are still negligible.
Transfer Characteristics
Transfer characteristics usually implies an input-output relationship, similar to the transfer function of a two-port network. But where are the input/output terminals or ports of a transistor? As we will see later on, one of the main goals of electronic circuits is to amplify signals (i.e. voltage, current, etc). Thus, it is convenient to choose the input-output terminal pair of a transistor that is commonly used to provide the largest amplification. In the BJT case, it is the common-emitter configuration, and in the MOSFET case, it is the common-source configuration.
The BJT Transfer Characteristic
The BJT common-emitter (CE) configuration is shown in Figure 1. We define the “input” signal as the base-emitter voltage, , and the “output” signal as the collector current . Therefore, we can model the the BJT transfer characteristic using
-
(1)
for a transistor in the forward-active region.[fn 1] Note that is the reverse saturation current of the collector-base junction and dependent on the type and geometry of the transistor, is the ideality factor, accounting for recombination in the base-emitter junction, is the Early Voltage, and , the voltage equivalent of temperature ( at ). For typical discrete (not integrated) BJTs, the value of is around , and since is typically much greater than , we can simplify Eq. (1) into
-
(2)
Eq. (1), shown in Figure 2, and superimposed with the transfer characteristic of the 2N2222A[1] NPN BJT, allows us to approximate the behavior of the “output” signal, in this case the collector current, when we change the base-emitter voltage, our “input” signal.
The MOSFET Transfer Characteristic
The MOSFET common-source (CS) configuration is shown in Fig. 3. As with the BJT, we define the “input” signal as the gate-source voltage, , and the “output” signal as the drain current, . Thus, the MOSFET transfer characteristic can be modeled as
-
(3)
in the saturation region.[fn 2] Note that is a constant dependent on the technology used in the manufacture, and the geometry, of the transistor, is the transistor threshold voltage, and is the channel length modulation coefficient. For typical discrete (not integrated) MOSFETs, , allowing us to approximate Eq. (3) with
-
(4)
And just like the BJT transfer characteristic, Eq. (3) allows us to model the behavior of the “output” signal, in this case the drain current, when we change the gate-source voltage, our “input” signal. Fig. 4 shows the transfer characteristic of a real MOSFET, together with the plot of Eq. (3).
Output Characteristics
In both the BJT and MOSFET, we defined our “output” as either the collector current or drain current. However, from Eqs. (1) and (3), we can see that both these “output” currents are also dependent on their respective “output” voltages -- the collector-emitter voltage, for the BJT and the drain-source voltage, for the MOSFET.
Since we want to be able to describe the transistor behavior completely, we need to take into account all the factors that affect the “output” current. Hence, we use the transistor output characteristic, vs. for a BJT and vs. for a MOSFET, to model the change in “output” current when the “output” voltage is changed.
The output characteristics of a typical BJT is shown in Fig. 5, and Fig. 6 shows the output characteristic of a typical MOSFET. Note that in both cases, the output characteristics span several operating regions. In the case of the BJT, the saturation, forward-active and cut-off regions can be seen. The same is true for the MOSFET, where the linear or ohmic region, the saturation region, and the sub-threshold region [fn 3] can be identified.
Input Characteristics
Since the BJT and MOSFET [fn 4] can be considered a three-terminal device, to completely describe all the currents and voltages, we will need 2 out of 3 voltages, and 2 out of 3 node currents. This means that in a BJT, if we know and , we automatically know the value of by KVL. By knowing the transfer and output characteristics, we can determine all the voltages in the BJT. The same is true for a MOSFET.
However, if we want to determine all the currents in the transistor, we need another set of current-voltage (I-V) characteristics. It turns out that the most convenient set of I-V characteristics for designing linear electronic amplifiers, is the “input” current vs. the “input” voltage characteristic. In BJTs, this is the vs. characteristic, and for the MOSFET, this is the vs. characteristic. For a BJT, by knowing and , we can easily determine using KCL. Again, the same is true for MOSFETs.
The input characteristics of a BJT can be derived from the BJT transfer characteristics. Since , we can just divide the BJT transfer characteristic by the transistor . [fn 5] The input characteristic of a MOSFET is trivial, since . [fn 6]
In summary, these large signal models allow us to determine the resulting transistor “input” and “output” DC currents when we apply DC voltages across the transistor terminals. Since we can obtain the DC values of the currents and voltages in a transistor, the large signal transistor models are typically used in what is called “DC Analysis”.
Small-Signal Modeling
As we have just seen, semiconductor-based transistors are very nonlinear -- exponential behavior for BJTs and quadratic behavior for MOSFETs, and these nonlinearities can vary significantly when going from one operating region to another. Analyzing circuits with these devices, by hand, using these large signal models, becomes very complex very quickly, especially when the number of transistors start to increase. Imagine writing your node or loop equations with exponentials and quadratic functions!
In order to analyze, and eventually design, linear electronic circuits, we use two very powerful tools: linearization, and two-port network reduction. These two tools will allow us to (1) use our linear circuit theory skills (taken up in EEE 31 and 33), and (2) break up complex circuits into smaller and simpler ones.
Linearizing the Transistor Transfer Characteristic
In many cases, and often by design, the input signal of an amplifier is made to change by a relatively small amount on top of its DC value. To determine the effect of this disturbance on the rest of the terminal voltages and currents, we can use the large signal models. However, this would result in rather complicated mathematical expressions, with limited intuitive value. We will use the linearization process to reduce the complexity of the computation, as well as get a better intuitive grasp of the circuit implications, but at the cost of a certain amount of error.
Consider an NPN BJT, in the forward-active region, that is biased with a DC base-emitter voltage of . This would result in a DC collector current , and from Eq. (2), is equal to
-
(5)
Note that we use the subscript Q to indicate that this is the quiescent [fn 7] point DC bias, meaning that this is the purely DC voltage and current of the BJT when there are no disturbances present.
Suppose we add a time-varying signal on top of , such that the total base-emitter voltage is now
-
(6)
Assuming that is small enough that the transistor does not change its operating region, the collector current then becomes
-
(7)
where is the collector current deviation away from its quiescent point, due to the addition of the “small” signal . Simplifying Eq. (7), and using Eq. (5), we get
-
(8)
As expected, is a nonlinear function (exponential) of . Now, let us try to linearize this relationship. Here we present two methods, but as we will see, they turn out to be equivalent.
Method 1
Recall, that any function that is infinitely differentiable, can be expressed as an infinite sum of terms, and that these terms are calculated from its derivatives at a certain point. We call this infinite sum the Taylor Series representation of a function, such that
-
(9)
where the function is expanded about point . Expanding , about , gives us the well known relationship
-
(10)
Thus, expanding , we get
-
(11)
Substituting Eq. (11) into Eq. (8) gives us
-
(12)
We can remove the DC quiescent current term I_{C,Q} from both sides of Eq. (12), giving us
-
(13)
Eq. (13) is a very important result. First, it gives us an alternative to Eq. (8) in computing for , but more importantly, it shows us that for , all the terms of Eq. (13) become very much less than the first term. Thus, we can approximate as
-
(14)
Note that Eq. (14) provides us with a “linear” relationship between and , and is a good approximation only when is small enough, that is when . In this case, we can assume that is a “small signal”. Eq. (13) also allows us to compute how much error we are incurring if we use Eq. (14), by summing up the remaining terms that we have ignored. Also, a very important observation here is that the relationship between and depends on DC quiescent current, .
Method 2
Another approach to linearizing the relationship between and is by looking at this relationship graphically. Consider the graph of a BJT transfer characteristic shown in Fig. [fig:Linearization-of-the-bjt-transfer-char].
If point is the DC quiescent point, then , and . Also, if , then adding on top of would result in the collector current also changing by an . We are using the absolute value signs to indicate that both and can take on negative values. That is, when , the total base-emitter voltage is . When is at its maximum value, , and the transistor is operating at point . When is at its minimum (negative) value, , corresponding to point .
For clarity, a possible time domain view is given in Fig. [fig:Time-domain-view] for and . Note that for time and , , thus, , which means that the transistor is in its quiescent point, that is and .
We can approximate the relationship between and using a straight line (linear!) passing through points and . If we know the slope, , of this line, we can estimate the magnitude given as . However, finding the slope of this line is not very straightforward, and as seen in Fig. [fig:Linearization-of-the-bjt-transfer-char], using the dashed line will result in errors for points between and . On the other hand, if is small, or equivalently if and , then the error becomes smaller, and our linear approximation becomes more accurate. The slope of our linear approximation, if we make approach zero, can be expressed as
-
(15)
Recall that for a function, , its derivative at a point is given as
-
(16)
Thus, for small values of , we can approximate as
-
(17)
where is known as the device or transistor transconductance, since it relates small variations in the base-emitter voltage and collector current -- the parameters of the transistor transfer characteristic. The transistor transconductance is formally defined as
-
(18)
Note that has units of Siemens (S)[fn 8], and is dependent on the quiescent point. Thus, a different would result in a different , and hence a different .
By plugging in Eq. [eq:bjt-simple-transfer] into Eq. [eq:gm-definition], we can calculate the value of the transconductance for a BJT as
-
(19)
Thus, Eq. [eq:bjt-gm] makes Eq. [eq:gm-slope] equivalent to Eq. [eq:ic-linear1], which should not be that surprising since the Taylor Series coefficients are obtained using derivatives and we are only approximating the transfer characteristic by the first derivative term.
We have just covered a very important concept: linearizing the BJT transfer function allows us to approximate the relationship of and using a linear function, given by Eq. [eq:gm-slope], instead of using Eq. [eq:ic-eq+small-signal-2], an exponential equation. Also, if the signals we are dealing with are made smaller, then the errors we incur when using this linear approximation is reduced.
So far, we have used the BJT transfer characteristic. The process is exactly the same when dealing with MOSFETs. We can derive the Taylor Series expansion of Eq. [eq:mos-simple-transfer] by just expanding the quadratic term
-
(20)
Since Eq. [eq:mos-simple-transfer] is already a polynomial, the Taylor Series representation shown in Eq. [eq:mos-expansion-transfer] is a finite series, and for our purposes, we group these terms into three. The first term in Eq. [eq:mos-expansion-transfer] is equal to . Therefore, we can write out the expression for using the remaining two terms
-
(21)
Again, if is small, then we can ignore the second term of Eq. [eq:mos-expansion-transfer-2], resulting in the linear relationship
-
(22)
If we use the definition of transconductance given in Eq. [eq:gm-definition], and apply it to the MOSFET transfer characteristic given in Eq. [eq:mos-simple-transfer], we would get
-
(23)
Using Eqs. [eq:mos-simple-transfer] and [eq:mos-gm-defn], we can derive the other common forms of the MOSFET transconductance
-
(24)
Once again, we see that our two linearization methods are equivalent, thus
-
(25)
It is very important to remember that even though is a function of the quiescent DC currents and voltages ( and , or and ), the linearized relationships using in Eqs. [eq:gm-slope] and [eq:mos-linearized-2] only relates the small signal disturbances superimposed on the DC signals, and , or and . Also, the linearization methods presented here are general techniques, independent of the transistor operating region, and can be applied to the large signal characteristic of any device that we may want to linearize.
The Small-Signal Equivalent Circuit
Notes
- ↑ In EEE 51, we will almost always use the BJT in the forward active region. However, in circuits where this is not the case, the transfer characteristic should be modeled with the appropriate relationship between and .
- ↑ In EEE 51, we will almost always use the MOSFET in the saturation region. However, in circuits where this is not the case, the transfer characteristic should be modeled with the appropriate relationship between and .
- ↑ It is a common simplification to assume that the drain current is zero when , putting the MOSFET in the “cut-off” region. However, keep in mind that below the threshold voltage, the MOSFET behaves like a BJT with very small currents. In very low-power applications, some MOSFETs are intentionally used in this sub-threshold region.
- ↑ In EEE 51, we will ignore the MOSFET body effect, and always assume that the body terminal is always connected to the source terminal.
- ↑ Note that this assumes is constant over . If the variation in is significant, then divide the transfer characteristic point-by-point with .
- ↑ This ignores MOSFET gate leakage, which will not be taken up in EEE 51.
- ↑ Synonymous to an idle, or rest state.
- ↑