Passive CMOS Devices

Passive devices such as resistors, capacitors, and inductors, are commonly used in biasing circuits, feedback networks, and signal or energy storage blocks. However, these passive devices, when built on fabrication processes that are optimized for transistors, may have characteristics different from their ideal or discrete counterparts. In this module, we examine the behavior of passive devices built alongside CMOS transistors.

Resistors

In standard digital CMOS processes, there is usually no provision for high resistance layers, since resistances are typically deemed bad for digital circuits. But in analog design, we often need well-controlled resistors, with relatively large resistance values.

Sheet Resistance

In order to evaluate if a particular layer could be used as to build a resistor, we look to their sheet resistance. Recall that for a resistor:

$R={\frac {\rho \cdot \ell }{A}}={\frac {\rho }{t}}{\frac {\ell }{w}}=R_{\mathrm {sh} }{\frac {\ell }{w}}$

(1)

Where $R_{\mathrm {sh} }$ is the sheet resistance of the layer, $\rho$ is the resistivity of the material, $\ell$ is the length along the direction of the current, and $A=w\cdot t$, is the cross sectional area normal to the current flow, which is equal to the product of the layer thickness, $t$ and $w$ is the width of the layer perpendicular to the current flow.

Note that the units of sheet resistance is $\mathrm {\Omega /\square }$ since $R_{\mathrm {sh} }$ is the resistance of a square, i.e. when $\ell =w$. Table 1 shows indicative sheet resistance values of the common conductive layers in a CMOS process:

Table 1: Sheet Resistances

Layer	Sheet Resistance
Metal	$50-70\,\mathrm {m\Omega /\square } \pm 30\mathrm {\%}$
Polysilicon	$5\,\mathrm {m\Omega /\square }$
$n^{+}$ or $p^{+}$ Diffusion	$5\,\mathrm {m\Omega /\square }$
$n$-well	$1-5\,\mathrm {k\Omega /\square } \pm 40\mathrm {\%}$

An illustrative cross-section of resistors using these layers are shown in Figs. 1 and 2.

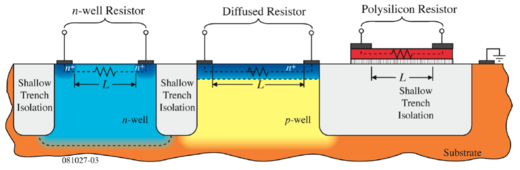Figure 1: Resistors built using semiconductor layers.

Figure 2: Resistors built using metal layers.

Figure 3: Silicide layers on diffusion and polysilicon layers to reduce the effective sheet resistance.

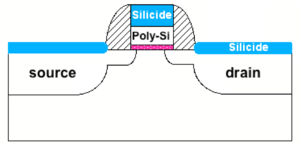
In a CMOS process optimized for digital circuits, the low sheet resistances of the semiconductor layers are due to a low-resistance silicide layer deposited on top of the semiconductor layer, as shown in Fig. 3. In analog CMOS processes, we are usually given the option to place a silicide block, i.e. to prevent the silicide layer from being deposited on specific locations on the die. Table 2 contains illustrative values of the sheet resistance of the semiconductor layers with the silicide block option.

Table 2: Non-Silicided Layer Properties

Layer	$R_{\mathrm {sh} }\,\mathrm {\Omega /\square }$	$T_{C}\,\mathrm {[ppm/^{\circ }C]}$	$V_{C}\,\mathrm {[ppm/V]}$	$B_{C}\,\mathrm {[ppm/V]}$
$n^{+}$-polysilicon	100
$p^{+}$-polysilicon	180
$n^{+}$-diffusion	50
$p^{+}$-diffusion	100
$n$-well	1000

Note that the non-silicided layers have significantly larger sheet resistances.

Temperature and Voltage Coefficients

In general, semiconductor resistor values change with temperature and applied voltage, and to describe these changes, we use temperature and voltage coefficients:

$R=R_{0}\left[1+T_{C}\left(T-T_{0}\right)+V_{C}\left(V_{1}-V_{2}\right)+B_{C}\left({\frac {V_{1}+V_{2}}{2}}-V_{B}\right)\right]$

(2)

Where $R_{0}$ is the nominal resistance value at some reference temperature $T_{0}$, $T_{C}$ is the temperature coefficient, $V_{C}$ is the voltage coefficient, $B_{C}$ is the body voltage coefficient, $V_{1}$ and $V_{1}$ are the terminal voltages, and $V_{B}$ is the bulk or body voltage.

In semiconductors, we know that the resistivity is a strong function of temperature, roughly due to two mechanisms:

1. Increasing the temperature increases the number of free carriers, thus lowering the resistance, resulting in negative temperature coefficients.
2. This increase in free carriers increases the probability of scattering events or collisions, increasing the effective resistance, resulting in positive temperature coefficients.