Shannon's Communication Theory

A First Look at Shannon's Communication Theory

Figure 1: A general communication system.

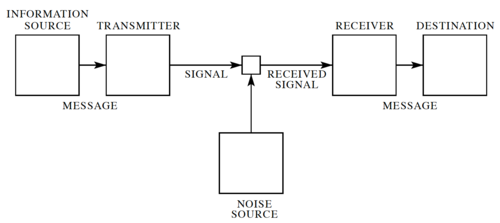
In his landmark 1948 paper, Claude Shannon developed a general model for communication systems, as well as a framework for analyzing these systems. The model has three components: (1) the sender or source, (2) the channel, and (3) the receiver or sink. The model also includes the transmitter that encodes the message into a signal, the receiver, for decoding the signal back into a message, as well the noise of the channel, as shown in Fig. 1.

In Shannon's discrete model, the source provides a stream of symbols from a finite alphabet, $A=\{a_{1},a_{2},\ldots ,a_{n}\}$, which are then encoded. The code is sent through the channel, which could be corrupted by noise, and when the code reaches the other end, it is decoded by the receiver, and then the sink extracts information from the steam of symbols.

Note that sending information in space, e.g. from here to there is equivalent sending information in time, e.g. from now to then. Thus, Shannon's theory applies to both information transmission and information storage.

Shannon's Noiseless Coding Theorem

One very important question to ask is: "How efficiently can we encode the information that we want to send through the channel?" To answer this, let us assume: (1) the channnel is noiseless, and (2) the receiver can accurately decode the symbols transmitted through the channel. First, let us define a few things.

A code is distinct if each codeword is distinguishable from every other, i.e. the mapping from source messages to codewords is one-to-one. A distinct code is uniquely decodable (UD) if every codeword is identifiable when immersed in a sequence of codewords.

Let $C=\{c_{1},c_{2},\ldots ,c_{r}\}$ be the alphabet of the channel, or in other words, the set of symbols that can be sent through the channel. Thus, encoding the source alphabet $A$ can be expressed as a function, $f:A\rightarrow C^{*}$, where $C^{*}$ is the set of all possible finite strings of symbols (or codewords) from $C$.

Let $\ell _{i}=\left|f\left(a_{i}\right)\right|$ where $i=1,2,\ldots ,n$, i.e. the length of the string of channel symbols encoding the symbol $a_{i}\in A$.

The Kraft-McMillan Inequality

A code with lengths $\ell _{1},\ell _{2},\ldots ,\ell _{n}$ is uniquely decodable if and only if:

$K=\sum _{i=1}^{n}{\frac {1}{r^{\ell _{i}}}}\leq 1$

(1)

To outline the proof, let's first evaluate $K^{m}$:

$K^{m}=\left(\sum _{i=1}^{n}{\frac {1}{r^{\ell _{i}}}}\right)^{m}=\sum _{i_{1}=1}^{n}\sum _{i_{1}=1}^{n}\cdots \sum _{i_{m}=1}^{n}{\frac {1}{r^{\ell _{i_{1}}+\ell _{i_{2}}+\ldots +\ell _{i_{m}}}}}$

(2)

Let $\ell =\max \left(\ell _{1},\ell _{2},\ldots ,\ell _{n}\right)$. Thus, the minimum value of $\ell _{i_{1}}+\ell _{i_{2}}+\ldots +\ell _{i_{m}}$ is $m$, when all the codewords are 1 bit long, and the maximum is $m\ell$, when all the codewords have the maximum length. We can then write:

$K^{m}=\sum _{k=m}^{m\ell }{\frac {N_{k}}{r^{k}}}$

(3)

Where $N_{k}$ is the number of combinations of $m$ codewords that have a combined length of $k$. Note that the number of distinct codewords of length $k$ is $r^{k}$. If this code is uniquely decodable, then each sequence can represent one and only one sequence of codewords.

Sources

• Tom Carter's notes on Information Theory