Difference between revisions of "Introduction to EE 229"
| (12 intermediate revisions by the same user not shown) | |||
| Line 28: | Line 28: | ||
{{NumBlk|::|<math>A_{P\mid \mathrm{dB}}=10\cdot\log_{10}\frac{P_\mathrm{out}}{P_\mathrm{in}}</math>|{{EquationRef|2}}}} | {{NumBlk|::|<math>A_{P\mid \mathrm{dB}}=10\cdot\log_{10}\frac{P_\mathrm{out}}{P_\mathrm{in}}</math>|{{EquationRef|2}}}} | ||
| − | In general, if <math>V_\mathrm{out}</math> appears across a load resistance, <math>R_L</math>, and <math>V_\mathrm{in}</math> is across an input resistance, <math>R_\mathrm{in}</math>, | + | [[File:2 port gain def.png|thumb|500px|Figure 2: A generic two-port circuit.]] |
| + | |||
| + | Consider the two-port circuit in Fig. 2. In general, if <math>V_\mathrm{out}</math> appears across a load resistance, <math>R_L</math>, and <math>V_\mathrm{in}</math> is across an input resistance, <math>R_\mathrm{in}</math>, | ||
{{NumBlk|::|<math>A_{P\mid \mathrm{dB}}=10\cdot\log_{10}\frac{P_\mathrm{out}}{P_\mathrm{in}} | {{NumBlk|::|<math>A_{P\mid \mathrm{dB}}=10\cdot\log_{10}\frac{P_\mathrm{out}}{P_\mathrm{in}} | ||
| Line 48: | Line 50: | ||
{{NumBlk|::|<math>V_{\mathrm{sig}\mid \mathrm{dBV}}=20\cdot\log_{10}\frac{V_\mathrm{sig}}{1\mathrm{V}}</math>|{{EquationRef|6}}}} | {{NumBlk|::|<math>V_{\mathrm{sig}\mid \mathrm{dBV}}=20\cdot\log_{10}\frac{V_\mathrm{sig}}{1\mathrm{V}}</math>|{{EquationRef|6}}}} | ||
| − | === Time Variance === | + | === Linearity === |
| + | '''Linear Systems''' are systems whose output can be expressed as a linear combination or ''superposition'' of its input components. Thus, if the system <math>f</math> is linear, and: | ||
| + | |||
| + | {{NumBlk|::|<math>y_1\left(t\right)=f\left[ x_1\left(t\right) \right]</math>|{{EquationRef|7}}}} | ||
| + | {{NumBlk|::|<math>y_2\left(t\right)=f\left[ x_2\left(t\right) \right]</math>|{{EquationRef|8}}}} | ||
| + | |||
| + | If we then apply a superposition of inputs: | ||
| + | |||
| + | {{NumBlk|::|<math>a\cdot y_1\left(t\right) + b\cdot y_2\left(t\right)=f\left[ a\cdot x_1\left(t\right) + b\cdot x_2\left(t\right) \right]</math>|{{EquationRef|9}}}} | ||
| + | |||
| + | The output should also be a linear combination of the original outputs, <math>y_1\left(t\right)</math> and <math>y_2\left(t\right)</math>. Systems that do not satisfy this condition are known as '''Nonlinear Systems'''. For example, if <math>y = f\left[x\right]= x^2</math>, then for <math>x_1 = 2</math>, <math>y_1 = 4</math>, and for <math>x_2 = 3</math>, we get <math>y_2 = 9</math>. The system is nonlinear since <math>y_1 + y_2 = 13 \ne \left(x_1 + x_2\right)^2 = 25</math>. | ||
| + | |||
| + | === Time-Variance === | ||
| + | In '''Time Invariant Systems''', when the input is shifted in time, the outputs are also shifted in time by the same amount. If <math>y\left(t\right)=f\left[x\left(t\right)\right]</math>, then for any arbitrary <math>\tau</math>: | ||
| + | |||
| + | {{NumBlk|::|<math>y\left(t -\tau\right) =f\left[ x\left(t-\tau\right) \right]</math>|{{EquationRef|10}}}} | ||
| + | |||
| + | Thus, it does not matter at what point in time the input is applied, the output is the same, except that it is shifted to the appropriate time relative to the input. | ||
| + | |||
| + | == The Submicron CMOS Transistor == | ||
| + | Before we proceed further, let's take a moment to review the CMOS fabrication process. | ||
| + | |||
| + | {{Note|[[229-A1.1 | '''Activity A1.1''' IC Frabrication]] -- This activity provides an overview of the CMOS fabrication process, and its future directions.|reminder}} | ||
| + | |||
| + | == Introduction to SPICE Simulation == | ||
| + | Simulation is a key tool in the analysis, design, and verification of analog and RF integrated circuits. In this class, we will use SPICE simulations extensively in our activities and projects. Thus, in preparation for our impedance matching activity, it is a good idea to go through a short tutorial on '''ngspice''' [[ngspice Tutorial|here]]. | ||
| + | |||
| + | In order to automate the analysis of our simulation results, we can use programming languages like Python. Please go over this [[Using Python with ngspice|tutorial]] on how to use Python in conjunction with SPICE simulations. | ||
== References == | == References == | ||
<references /> | <references /> | ||
Latest revision as of 22:48, 13 September 2020
Welcome to EE 229!
Since we are offering this class remotely, there will be many changes to our normal course delivery:
- There will be no face-to-face lecture classes. All the material will be made available via this site.
- There will be more emphasis on student-centric activities, e.g. analysis, design, and simulations. Thus, you will be mostly "learning by doing". In this context, we will set aside an hour every week for consultations and questions via video-conferencing.
- Grades will be based on the submitted deliverables from the activities. Though we will not be very strict regarding the deadlines, it is a good idea to keep up with the class schedule and avoid cramming later in the semester.
Let's get started!
Contents
The Design of RF Transceivers
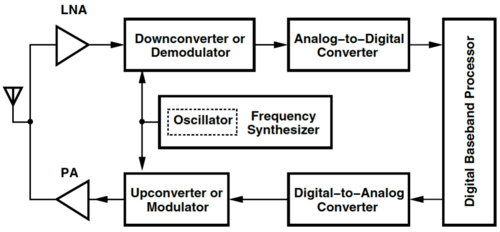
The objective of an RF transceiver is to transmit and receive information. To perform this task, however, requires concepts, technologies, and interactions from and among many fields, and some of these fields might not directly related to IC design. The task itself is relatively complex, with trade-offs and optimizations spanning various domains and levels of abstractions.
Fig. 1 shows a generic RF transceiver block diagram, showing:
- The transmit path, showing of basic system components needed to convert digital data into its analog form, modulate the signal, up-convert it from baseband to some center frequency, and finally send it to the antenna using a power amplifier.
- The receive path, where the signal is detected the low-noise amplifier, then down-converted back to baseband from a certain center frequency, then converted into the appropriate digital representation in preparation for further processing.
A Short Review
The goal of this module is to review the basic concepts of RF design, leading our coverage of communication systems, and then to transceiver architectures. These concepts and ideas will serve as the backdrop for analysis and design of RF circuits, allowing us to optimize our circuits for specific environments, contexts, and situations.
Power and Gain
The RF receiver subsystem is normally designed to detect and amplify signals that are at low power and voltage levels, while the transmitter subsystem is designed to deliver a sufficient amount of power to the antenna, enough to be detected at the remote receiver. Thus, we are very interested in the power and voltage gains of the blocks. Since we deal with a very large range of values, from microwatts for receivers to hundreds of watts for transmitters, it becomes convenient to express the voltage and power ratios or gains in terms of decibels (dB).
-
(1)
-
-
(2)
-
Consider the two-port circuit in Fig. 2. In general, if appears across a load resistance, , and is across an input resistance, ,
-
(3)
-
If , then:
-
(4)
-
We can also express absolute values of power or voltage in this form, but instead of comparing it to another signal, we compare it to a reference level. For example, we can express signal power in dBm instead of watts by comparing the signal power, to 1 mW:
-
(5)
-
We can also express voltages in dBV instead of volts:
-
(6)
-
Linearity
Linear Systems are systems whose output can be expressed as a linear combination or superposition of its input components. Thus, if the system is linear, and:
-
(7)
-
-
(8)
-
If we then apply a superposition of inputs:
-
(9)
-
The output should also be a linear combination of the original outputs, and . Systems that do not satisfy this condition are known as Nonlinear Systems. For example, if , then for , , and for , we get . The system is nonlinear since .
Time-Variance
In Time Invariant Systems, when the input is shifted in time, the outputs are also shifted in time by the same amount. If , then for any arbitrary :
-
(10)
-
Thus, it does not matter at what point in time the input is applied, the output is the same, except that it is shifted to the appropriate time relative to the input.
The Submicron CMOS Transistor
Before we proceed further, let's take a moment to review the CMOS fabrication process.
Introduction to SPICE Simulation
Simulation is a key tool in the analysis, design, and verification of analog and RF integrated circuits. In this class, we will use SPICE simulations extensively in our activities and projects. Thus, in preparation for our impedance matching activity, it is a good idea to go through a short tutorial on ngspice here.
In order to automate the analysis of our simulation results, we can use programming languages like Python. Please go over this tutorial on how to use Python in conjunction with SPICE simulations.
References
- ↑ Behzad Razavi, RF Microelectronics (2nd Edition), Prentice Hall Press, 2011, USA.














![{\displaystyle y_{1}\left(t\right)=f\left[x_{1}\left(t\right)\right]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/c5114e826b54fda1146c8fba99f44414346333e8)
![{\displaystyle y_{2}\left(t\right)=f\left[x_{2}\left(t\right)\right]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/ddb476700c1df88dcc53f470c0376a733125a017)
![{\displaystyle a\cdot y_{1}\left(t\right)+b\cdot y_{2}\left(t\right)=f\left[a\cdot x_{1}\left(t\right)+b\cdot x_{2}\left(t\right)\right]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/4a94b9c3469a6f60b2256a501bfe044eabec6bcd)


![{\displaystyle y=f\left[x\right]=x^{2}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/12e08820371781362501bd0a01168b695859d372)





![{\displaystyle y\left(t\right)=f\left[x\left(t\right)\right]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/58e7e4407ee505d5598e60c4d1fd06300b9fa1dd)

![{\displaystyle y\left(t-\tau \right)=f\left[x\left(t-\tau \right)\right]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/52821c125f6a7750d47c0618ff322d3a6644483c)