Source coding

A First Look at Shannon's Communication Theory

Figure 1: A general communication system.

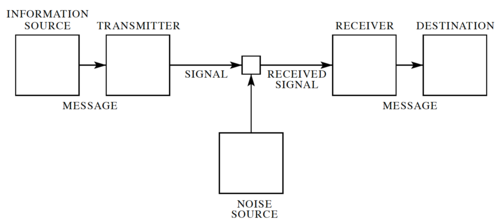
In his landmark 1948 paper, Claude Shannon developed a general model for communication systems, as well as a framework for analyzing these systems. The model has three components: (1) the sender or source, (2) the channel, and (3) the receiver or sink. The model also includes the transmitter that encodes the message into a signal, the receiver, for decoding the signal back into a message, as well the noise of the channel, as shown in Fig. 1.

In Shannon's discrete model, the source provides a stream of symbols from a finite alphabet, ${\mathcal {X}}=\{x_{1},x_{2},\ldots ,x_{n}\}$, which are then encoded. The code is sent through the channel, which could be corrupted by noise, and when the code reaches the other end, it is decoded by the receiver, and then the sink extracts information from the steam of symbols.

Note that sending information in space, e.g. from here to there is equivalent sending information in time, e.g. from now to then. Thus, Shannon's theory applies to both information transmission and information storage.

Source-channel Separation Theorem

One of the important questions in information theory is determining the maximum amount of information that can be reliably communicated over a channel. Right now, we are dealing with source coding in which our goal is to provide error-free data compression. That is, we aim to produce the shortest possible representation of information. The next half of the communication framework, channel coding, will be discussed in Module 4. In that section, we will find out the minimum additional redundancy that we need to add to reliably communicate information.

The source-channel separation theorem, informally speaking, is a statement which says that the maximum amount of information can be communicated over a channel by separately optimizing the source coding scheme and the channel coding scheme. In other words, there is no performance penalty for being greedy and trying to obtain the best possible source code.

Source codes

Simply put, a source code ${\mathcal {C}}$ is a mapping from an input alphabet ${\mathcal {X}}$ to another alphabet ${\mathcal {D}}$, which is the set of codewords. If we let $D=|{\mathcal {D}}|$, then we can say that ${\mathcal {C}}$ is a D-ary code. A source code ${\mathcal {C}}$ can be extended so that sequences of symbols drawn from ${\mathcal {X}}$ are encoded as the concatenation of the individual encodings of each source symbol. For example, consider the source alphabet ${\mathcal {X}}=\{1,2,3,4\}$. The source code

$x$	1	2	3	4
${\mathcal {C}}(x)$	0	010	01	10

will have an extension ${\mathcal {C}}^{*}$ which will map the sequence $2,1,3$ to 010001.

The given definition, by itself, is so general that it may include codes that barely have any practical use. For example, from the definition it is possible to have a code which maps every symbol to 0. You should see that such a code is useless since there is no way to recover the original symbols from a stream of zeros. A code ${\mathcal {C}}$, such as the example just now, is called singular if there exists distinct symbols $x_{1},x_{2}\in {\mathcal {X}}$ such that ${\mathcal {C}}(x_{1})={\mathcal {C}}(x_{2})$. Whenever a code ${\mathcal {C}}$ produces a one-to-one mapping between ${\mathcal {X}}$ and ${\mathcal {D}}$, we will call such a code nonsingular.

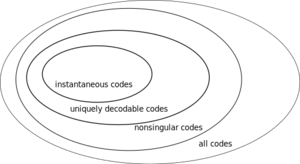
As a preview, below is a list of increasingly stricter classes of source codes:

• nonsingular: if ${\mathcal {C}}(x_{1})\neq {\mathcal {C}}(x_{2})$ whenever $x_{1}\neq x_{2}$.
• uniquely encodable: if the extension ${\mathcal {C}}^{*}$ of ${\mathcal {C}}$ is nonsingular.
• instantaneous: if no codeword is a prefix of another codeword.

Uniquely encodable codes produces encodings that can only correspond to a unique sequence of input symbols. The code presented above is nonsingular, but not uniquely encodable because the encoding 0100 can be obtained from either $(2,1)$ or $(3,1,1)$. The table below shows representative examples of each class of source code.

$X$	singular	nonsingular but not uniquely encodable	uniquely encodable but not instantaneous	instantaneous
1	0	0	10	0
2	0	010	00	10
3	0	01	11	110
4	0	10	110	111

At the strictest end, instantaneous codes are among the easiest to decode since the prefix-free condition ensures that one can decode a sequence by reading left to right. To get a better feel of the convenience brought by instantaneous code, please try the exercise below.

Checkpoint: Use the "uniquely encodable, but not instantaneous" code to decode the following bitstring: 1101100000111000101111.

Expected Length

In source coding, we aim to compress information losslessly. In general, a $D$-ary code ${\mathcal {C}}$ will consists of codewords of different lengths $l_{1},l_{2},...,l_{m}$. When used to encode samples of a random variable $X$, the expected length is given by

$L=\sum _{i}p_{i}l_{i},$

where $l_{i}$ is the length of the codeword corresponding to a source symbol $x_{i}\in {\mathcal {X}}$. Always keep in mind that the length of the codeword is in terms of the symbols used in the $D$-ary alphabet of ${\mathcal {C}}$.