Engaging introduction to information theory

What's with information theory?

If Newton developed theories for calculus and Einstein developed the theory of relativity, then Claude Shannon, at par with these mathematical geniuses, developed information theory. In 1948, Claude's published work called "A Mathematical Theory of Communication" tells us how to quantify information. IBased on any dictionary, information can mean knowledge, facts, or a message obtained from investigation, study, or instruction. Information in a mathematical perspective means something similar but with a tiny twist in its definition. Let's take a look at a few examples. Suppose you were told the following:

1. Classes will start next week!
2. The entire semester will be suspended due to the pandemic!
3. AEKG EAKJGRALGN EAFKEA EAFFH

Can you identify which statement conveys the most information? Hopefully, you'll pick statement number 2! If you carefully think about it, the first statement is probably something you know already. It has a high probability of happening, but this information isn't new to you. For the second statement, the chance of this happening is almost close to none, and we'll be the most surprised if it does happen! The second statement, surprisingly, has the most information. Lastly, the third statement is just a jumble of letters without structure; therefore, it has no meaning at all. In the perspective of the English language, the third statement has a very low chance of happening because we know very well that this is not how we structure our sentences in English.

The example above tells us something about information. Information consists of surprise and meaning. In this class, we are more interested in the surprise part of information because that is something that we can measure. There are two motivations for this : (1) SOriginally, Shannon's information theory was developed for communication systems, and 'surprise' was more relevant. (2) Meaning or semantics are challenging problems. We won't discuss meaning for now but for those interested you might want to check out the branch of artificial intelligence called natural language processing (NLP). The above example is oversimplified, but it should give you a glimpse of what we expect when studying information theory. Let's take a look at a few more interesting examples.

A tale of 2ⁿ paths

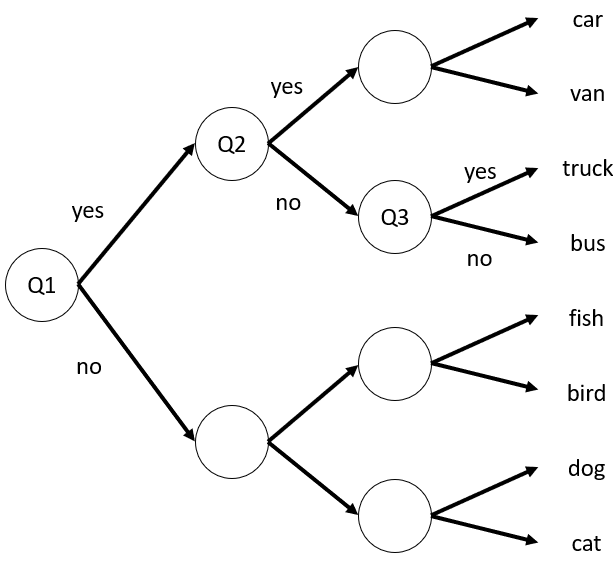
When you were young, you've probably come across a game called Pinoy Henyo. Pinoy Henyo was an iconic game in the Philippines consisting of two players: (1) a guesser and (2) an answerer. The guesser will have a random word stuck on his forehead, and only the answerer can see the word. The word could be an object, thing, place, or person. The goal is that the guesser asks a series of questions to which the answerer can only respond with a yes or no until the guesser can correctly guess the word. In other countries this game is also called twenty questions. Let's try to constrain the game to three questions only, and let's assume that the guesser and answerer know the eight possible words. The goal is to guess the word that the answerer thought of. Consider the figure below that shows possible paths to the correct.

In the figure, all arrows that point up are 'yes' while all arrows that point down are 'no'. Let's say our ideal set of questions would be:

1. Q1 - Is it a vehicle?
2. Q2 - Is the size small?
3. Q3 - Does it carry things?

We get one step closer to the correct answer for every question. Since the questions are answerable only by yes or no, we always obtain a 'bit' of information (pun intended). For example, when we asked Q1, and the answerer responded with a yes, we now have 1 bit of information. That information tells us that we are thinking of a vehicle. When we asked Q2, we received another bit of information. That information tells us that the automobile is small. Finally, when we get to Q3, we receive another bit of information again. If you were asked to repeat the game, you would still ask 3 questions that lead to one of the 8 possible answers. In principle, each question you ask halves the number of possible answers as depicted in the figure. As the guesser, each answer has an equal 'surprise' for you, but it is beneficial because each response gives you information! Are you starting to see a pattern now?

Our simple three-question example tells us that it takes $n$ questions to come up with $2^{n}$ different answers. In the case of the twenty questions game, we can arrive at $2^{20}=1,048,576$ different possible outcomes. This is an extreme number. The Pinoy Henyo game is more challenging because we have no idea how many $n$ questions do we need yet the challenge is to get to the final answer with the least number of questions or at least until time runs out. In information theory, we are interested in "what question would give me the highest information?". If you carefully think about it, in Pinoy Henyo, you would like your partner (i.e., answerer) to actually give you a yes rather than a no. The context looks different because we're expecting so many 'no's because we know that most of our questions may not be useful. However, when we receive a 'yes' it becomes surprising because it gives us valuable information. Doesn't this sound familiar with our oversimplified example above? Think about it.

Try to play a game of Pinoy Henyo with a friend or family member. While you're playing, try to ponder on how information theory can actually help you?

A simple case of data compression

Information theory was developed in the context of communication. The original problem it tries to solve is how to maximize the transmission of data over some channel. Let's try to understand this through a simple example. Imagine that some guy, named Bob, wants to express his love for Alice who lives miles away. Since a picture is worth a thousand words, and Bob decides to go the extra mile, he sends an animated video with 1080p quality running at 30 frames per second (FPS). For now, let's assume that their only means of communication is through a satellite with very little bandwidth (i.e., the satellite communication can only transfer 19.2 million bit/s). The GIF below shows a cute animation of this.

Let's do a bit of math. Each frame of the video is one image. Each image consists of three color channels: RGB. Each color channel consists of $1920\times 1080$ pixel dimensions, and each pixel ranges from $0-255$ which is equivalent to $\log _{2}(255)=8$ bits per pixel. In total, one image consists of $3\times 1920\times 1080\times 8=49,766,400$ bits of information. Moreover, the video runs in 30 FPS so the rate of data that needs to be transmitted over the satellite channel is $30\times 49,766,400\approx 1.5\times 10^{9}$ or $1.5\ {\textrm {billion}}$ bits per second. Clearly, 30 images per second cannot fit in the satellite channel that can only support 19.2 million bit/s. If this happens, Alice needs to buffer the images on her side (i.e., wait a bit until the entire video has loaded).