Engaging introduction to information theory

What's with information theory?

If Newton developed theories for calculus and Einstein developed the theory of relativity, then Claude Shannon, at par with these mathematical geniuses, developed information theory. In 1948, Claude's published work called "A Mathematical Theory of Communication" made this mathematical framework where we can quantify information. Information based on any dictionary can mean knowledge, facts, meaning, or even a message that was obtained from investigation, study, or instruction. Information in a mathematical sense can mean something similar but with a little twist in its definition. Let's take a look at a few examples. Suppose you were told the following:

1. Classes will start next week!
2. The entire semester will be suspended due to the pandemic!
3. AEKG EAKJGRALGN EAFKEA EAFFH

If we ask you identify which of the statements convey the most information, hopefully you'll pick statement number 2! If you think about it carefully, the first statement is probably something you know already. It has a high probability of happening but this information isn't new to you. For the second statement, the probability of this happening is almost close to none and we'll be the most surprised if it does happen! The second statement, surprisingly, has the most information. Lastly, the third statement is just a jumble of letters that is meaningless and therefore has no meaning at all. In the perspective of the English language, the third statement has very low chance of happening because we know very well that this is not how we structure our sentences in English.

The example above tells us something about information. Information consists of surprise and meaning. In this class, we'll be more interested in the surprise part of information because that is something that we can measure. There are two motivations for this : (1) Shannon's information theory was originally developed for communication systems and 'surprise' was more relevant. (2) Meaning or semantics is a challenging problem. We won't discuss it for now but for those interested you might want to check out the branch of artificial intelligence called natural language processing (NLP). The above example is oversimplified but it should give you a glimpse of what we expect when we study information theory. Let's take a look at a few more interesting examples.

A tale of 2ⁿ paths

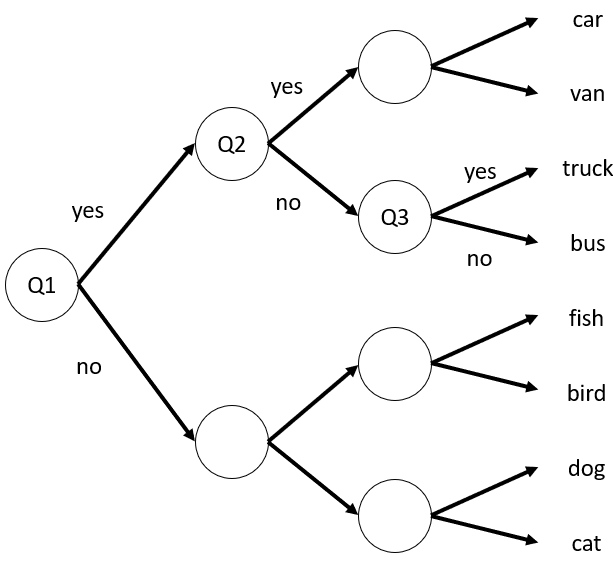
When you were young, you've probably come across a game called Pinoy Henyo. Pinoy henyo was an iconic game in the Philippines that involves two players: (1) a guesser and (2) an answerer. The guesser will have a random word stuck on his forever which only the answerer can see. The word could be an object, thing, place, or a person. The goal is that the guesser asks a series of questions to which the answerer can only respond with a yes or no until the guesser can correctly guess the word. In other countries this game is also called twenty questions. Let's try to constrain the game to three questions only and let's assume that the guesser and answerer knows the eight possible words. Your goal is to guess what the answerer is thinking. Consider the figure below which shows the possible path.

In the figure, all arrows that point up are 'yes' while all arrows that point down are 'no'. Let's say our ideal set of questions would be:

1. Q1 - Is it a vehicle?
2. Q2 - Is the size small?
3. Q3 - Does it carry things?

For every question we ask, we are one step closer to the correct answer. Since the questions are answerable only by yes or no, then it's as if we always obtain a bit of information (pun intended) for every question we ask. For example, when we asked Q1, and the answerer responded with a yes, we have obtained 1 bit of information. When we asked Q2, we get another 1 bit of information. Finally, when we get to Q3, we get 1 bit of information again. If you were asked to repeat the game, you would still ask 3 questions that lead to one of the 8 possible answers. In principle, each question you ask halves the total number of possible answers as depicted in the figure. As the guesser, each answer has an equal 'surprise' for you but it is beneficial to you because each answer gives you information! Are you starting to see a pattern now?

Our simple three question example tells us that it takes $n$ questions to come up with $2^{n}$ different answers. In the case of the twenty questions game, we can arrive at $2^{20}=1,048,576$ different possible outcomes which is an extreme number. The Pinoy Henyo game is more challenging because we have no idea how many $n$ questions do we need yet the challenge is to get to the final answer with the least number of questions or at least until time runs out. In information theory, we are interested in "what question would give me the highest information?". If you think about it carefully, in Pinoy Henyo, you would like your partner (i.e., answerer) to actually give you a yes rather than a no. The context looks different because we are expecting so many 'no's because we know that most of our questions may not be useful. However, when we receive a 'yes' it's surprising and that gives us valuable information. Doesn't this sound familiar with our oversimplified example above? Think about it.

Try to play a game of Pinoy Henyo with a friend or family member. While you're playing, try to ponder on how information theory can actually help you?