Difference between revisions of "161-A1.2"
Adrian Vidal (talk | contribs) |
Adrian Vidal (talk | contribs) |
||
| Line 136: | Line 136: | ||
===Task description=== | ===Task description=== | ||
| − | For your first graded programming exercise, you are to write a function <code> | + | For your first graded programming exercise, you are to write a function <code>estimated_mutual_information</code> which will take one argument, <code>xy_samples</code>, which is a list of <code>tuple</code> objects corresponding to pairs of samples <math>(X,Y)</math>. From the list of tuples, the function should return a <code>float</code> corresponding to the estimated mutual information <math>I(X;Y)</math>. To make things simple, you may assume <math>X</math> and <math>Y</math> are integers. |
The header script for Exercise 1 will simply import the <code>math</code> module. During testing, the following Python script will run: | The header script for Exercise 1 will simply import the <code>math</code> module. During testing, the following Python script will run: | ||
| Line 152: | Line 152: | ||
| | | | ||
<syntaxhighlight lang="python3"> | <syntaxhighlight lang="python3"> | ||
| − | def | + | def estimated_mutual_information(xy_samples): |
# your code.. | # your code.. | ||
# more code.. | # more code.. | ||
Revision as of 21:58, 6 March 2021
Contents
A unified view of random variables
In EEE 137, you were first introduced to a single random variable and then later taught to deal with multiple random variables. Fortunately, information theory allows us to detach ourselves from the specific values taken by a random variable and simply examine the "amount" of randomness it contains. In this course, we can afford to be indifferent between a random variable that has a 50-50 chance of being a head or a tail (a coin toss), and another random variable that has a 50-50 chance of being sunny or rainy (a weather forecast). As far as information theory is concerned, "heads"/"tails," and "sunny"/"rainy" are just labels.
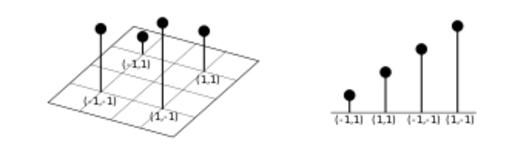
Under the mindset that labels do not matter (please do not take this too seriously and carelessly drag it out of current context), the next example aims to illustrate that a pair of random variables can be treated as if it was a single random variable. Consider a discrete random variable over the alphabet and the probability mass function (pmf) ,
|
|
1 |
2 |
3 |
4 |
|
|
0.1 |
0.2 |
0.3 |
0.4 |
Now, consider a pair of random variables where Y takes values from and Z takes values from . Suppose that the following joint pmf:
| 0.3 | 0.1 | |
| 0.4 | 0.2 |
Our new-found mindset allows us to realize that the array above is simply a rearrangement of the probability weights 0.1, 0.2, 0.3 and 0.4. Indeed, we can go so far as to produce the following stem plot.
Entropy and conditional entropy
With a unified view of random variables, we are now equipped to look at the entropy of both (single) random variables and jointly distributed random variables.
For our discussion in this course, we can just look at the entropy as a function of individual probability masses. The only difference is that for jointly random variables, the alphabet can be large in general due to the number of possible pairs between the two alphabets and . In essence, working with more random variables simply means that we will have to spend more time calculating it. The beauty of the underlying mathematics here lies in its power to make simple, succinct statements that holds true for many cases even without the need to calculate individual terms.
Again, we use our unified view in discussing conditional entropy. From the expression H(X|Y), it should now be straightforward to extend the results to "heavier" expressions like , , or .
Consider fixing Y=y. The marginal probabilities produce a valid probability mass function in its own right, and hence we can calculate the (regular) entropy . This tell us that by covering all possible values , we will obtain values.
For example,
| 0.1 | 0.2 | |
| 0.3 | 0.4 |
We can simulate sampling, say 20 pairs, from this joint distribution by using the following code:
import random
samples = random.choices([(0,0), (0,1), (1,0), (1,1)], weights=[0.1, 0.2, 0.3, 0.4], k=20)
which might generate the following list
[(0, 1), (0, 1), (1, 1), (0, 1), (1, 1), (1, 1), (1, 0), (1, 0), (1, 1), (1, 1), (0, 1), (1, 0), (1, 0), (1, 1), (1, 1), (1, 1), (1, 0), (1, 0), (1, 1), (0, 1)]
If we want to inspect , we need to "categorize" the samples into those that have Y=0,
y0_samples = [(1, 0), (1, 0), (1, 0), (1, 0), (1, 0), (1, 0)]
and those that have Y=1,
y1_samples = [(0, 1), (0, 1), (1, 1), (0, 1), (1, 1), (1, 1), (1, 1), (1, 1), (0, 1), (1, 1), (1, 1), (1, 1), (1, 1), (0, 1)]
From the observed samples alone, we produce the following estimates:
- For , we estimate the conditional entropy as .
- For , we estimate the conditional entropy as .
Note that is estimated as zero because when we only look at the samples where , does not exhibit any variation at all! In y1_samples, there are five pairs where and nine pairs where , from which we estimate conditional distribution of given to be , which has an entropy of around 0.9403 (using base-2 logarithms).
The expression uses the probability distribution of Y to add greater weight to more probable values. In our example, since there are six pairs where and 14 pairs where . Based on the observed samples, we might estimate that and . At this point, conditional entropy should be now intuitive in the following sense: if we fix to some value, we induce a (conditional) probability distribution over which corresponds to some entropy . To get the overall conditional entropy, we take the weighted average of for different values of :
At this point, it is helpful to outline the process we just did:
- For each possible value , we calculate
- Calculate as the weighted average of the values using the probability as weights.
From this specific example, the following general expression should now make sense:
Simulating a random source
As shown in the previous section, we can use Python to create such a source of randomness. From our 20 sampled pairs, we can estimate , but from the joint distribution, we can calculate the exact value , rounded to three decimal places. This means our estimate is off by around 25% ! Fortunately, it is possible to use many samples to reach the true value as close as possible. That such precision is possible is a consequence of the law of large numbers.
The law of large numbers is an optimistic statement that promises us that we can estimate the probability of an event that can be very close to the true value with very small variance. A close inspection of the definition of information measures reveals that they all boil down to obtaining the necessary probabilities. Hence, if we have an accurate way of estimating the required probabilities, we can also estimate the information measures quite accurately. If we want to reap the guarantee granted by the law of large numbers, we must have a way of generating independent and identically distributed samples.
Nowadays, producing high-quality sources of randomness is made easy since they often come shipped with many of your favorite applications, from numerical software to spreadsheets or even photo-editing software. The Mersenne Twister, which forms the backbone of many of these sources, generate close to uniformly random bitstreams that can be post-processed and be "shaped" to a wide family of probability distributions.
Exercise 1.1: Estimating mutual information (9 points)
With a fairly reliable source of randomness, it is now up to us to estimate information measures from the samples. This is useful when we want to reason about the amount of randomness in certain variables. Mutual information, in particular, finds it use in reasoning about how much information we can obtain about a given random variable by observing another random variable .
Task description
For your first graded programming exercise, you are to write a function estimated_mutual_information which will take one argument, xy_samples, which is a list of tuple objects corresponding to pairs of samples . From the list of tuples, the function should return a float corresponding to the estimated mutual information . To make things simple, you may assume and are integers.
The header script for Exercise 1 will simply import the math module. During testing, the following Python script will run:
| Header |
import math
|
| Student submission (function only) |
def estimated_mutual_information(xy_samples):
# your code..
# more code..
return ans
}
|
| Main test script |
# Main test script goes here, and will not be visible to students.
# The script will test if the submitted code does the prescribed functionality.
# For successfully validated scripts, test results will be sent via email.
|
Please be careful not to call functions imported from libraries not specified in the header script. Doing that will cause the program to throw a NameError. Accessing global variables will similarly cause an error.
Do not include I/O commands such as input, print, or open. The validator script will return an error upon detecting usage of such functions.
Sample input
Here are some small test cases that you may try:
| Input list | Return value |
[(0,0),(0,1),(1,0),(1,1)]
|
0.0
|
[(0,0),(0,1),(1,0)]
|
0.25162
|
[(0,0),(1,1)]
|
1.0
|
In your code, make sure that you use base-2 logarithm in your calculations.
Exercise 1.2: Conditional entropy (1 point)
Let and be jointly distributed with the following distribution:
| 0 | 1/3 | |
| 1/6 | 1/2 |
Now, consider a new random variable which is defined as the XOR of and . Calculate the conditional entropy .































![{\displaystyle [5/14,9/14]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/b3fecd7b7f8e2a05d3e413fb256553834557285e)











