Difference between revisions of "2S2122 Activity 3.1"
Ryan Antonio (talk | contribs) |
Ryan Antonio (talk | contribs) |
||
| Line 92: | Line 92: | ||
== Problem 3 - CRAZY Channels == | == Problem 3 - CRAZY Channels == | ||
| − | === Problem 3.a Binary Erasure Channel === | + | === Problem 3.a Binary Erasure Channel (2 pts.) === |
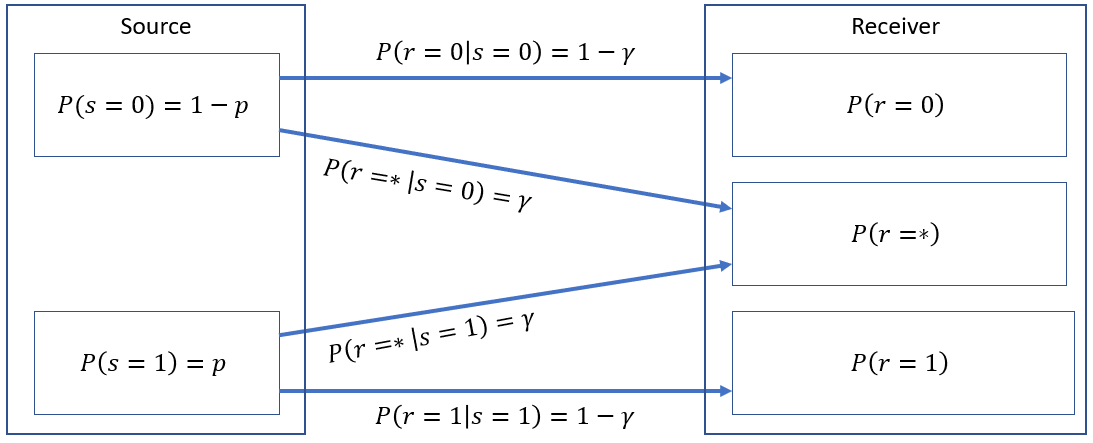
A '''Binary Erasure Channel (BEC)''' is shown below: | A '''Binary Erasure Channel (BEC)''' is shown below: | ||
| Line 101: | Line 101: | ||
| − | 1. | + | 1. Fill up the table below but show your solutions. Solve for each probability first then summarize your results in the table. Answers should be in terms of <math> p </math> and <math> \gamma </math> only. (0.2 pts. each term) |
| − | + | {| class="wikitable" | |
| − | + | |- | |
| + | ! scope="col"| Probability Term | ||
| + | ! scope="col"| Function | ||
| + | |- | ||
| + | | style="text-align:center;" | <math> P(r=0) </math> | ||
| + | | style="text-align:center;" | | ||
| + | |- | ||
| + | | style="text-align:center;" | <math> P(r=1) </math> | ||
| + | | style="text-align:center;" | | ||
| + | |- | ||
| + | | style="text-align:center;" | <math> P(r=*) </math> | ||
| + | | style="text-align:center;" | | ||
| + | |- | ||
| + | |} | ||
| + | 2. Determine the '''mutual information on a per outcome basis'''. Fill up the table below but show your solutions. Answers should be in terms of <math> p </math> and <math> \gamma </math> only. (0.2 pts. each term) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! scope="col"| Probability Term | ||
| + | ! scope="col"| Function | ||
| + | |- | ||
| + | | style="text-align:center;" | <math> I(r=0,s=0) </math> | ||
| + | | style="text-align:center;" | | ||
| + | |- | ||
| + | | style="text-align:center;" | <math> I(r=1,s=1) </math> | ||
| + | | style="text-align:center;" | | ||
| + | |- | ||
| + | | style="text-align:center;" | <math> I(r=*|s=0) </math> | ||
| + | | style="text-align:center;" | | ||
| + | |- | ||
| + | | style="text-align:center;" | <math> I(r=*|s=1) </math> | ||
| + | | style="text-align:center;" | | ||
| + | |- | ||
| + | |} | ||
| + | 3. What is the average mutual information <math> I(R,S) </math>? (0.2 pts.) | ||
| + | |||
| + | 4. What is the maximum channel capacity <math> C </math>? When does it happen? (0.2 pts.) | ||
| + | |||
| + | 5. What are the pros and cons of BEC compared to BSC? Let's assume <math> \gamma </math> is channel noise. (0.2 pts.) | ||
=== Problem 3.b Binary Error and Erasure Channel === | === Problem 3.b Binary Error and Erasure Channel === | ||
Revision as of 19:53, 2 March 2022
Contents
Problem 1 - The Complete Channel Model (2 pts.)
Answer comprehensively and do the following:
1. Draw the complete channel model. (0.2 pts)
2. What is the source? (0.2 pts)
3. What is the channel? (0.2 pts)
4. What is the receiver? (0.2 pts)
5. What are the encoder and decoder? (0.2 pts)
6. What are codebooks? (0.2 pts)
7. What is coding efficiency? (0.2 pts)
8. What is the maximum capacity of a channel? (0.4 pts)
9. What are symbol rates? (0.4 pts)
10. Where is Waldo? (if we like your answer you get 0.2 pts extra)
Problem 2 - Review of BSC (2 pts.)
1. Draw the BSC channel with correct annotations of important parameters and . (0.1 pts) 2. Fill up the probability table in terms of the important parameters: (0.1 pts each entry)
| Probability Term | Function |
|---|---|
3. Fill up the table below with the measures of information. Answer only in terms of and parameters (and of course constants). When necessary you can use "let be ...". Also, answer with equations that are programming friendly. Answering the simplified version merits half points for that part. (0.1 pts per term)
| Information Measure | Function |
|---|---|
4. Explain why when regardless of varying the source probability distribution . (0.2 pts.) 5. Explain what does negative information mean and when can it happen? (0.2 pts.) 6. Explain why means information from the receiver can short-circuit back to the source. (0.1 pts.)
Problem 3 - CRAZY Channels
Problem 3.a Binary Erasure Channel (2 pts.)
A Binary Erasure Channel (BEC) is shown below:
BEC is an interesting channel because it has 3 different outputs. The received values , , and . This channel assumes that we can erase or throw unwanted values into the trash bin. It's worth investigating! 😁 Show your complete solutions and box your final answers.
1. Fill up the table below but show your solutions. Solve for each probability first then summarize your results in the table. Answers should be in terms of and only. (0.2 pts. each term)
| Probability Term | Function |
|---|---|
2. Determine the mutual information on a per outcome basis. Fill up the table below but show your solutions. Answers should be in terms of and only. (0.2 pts. each term)
| Probability Term | Function |
|---|---|
3. What is the average mutual information ? (0.2 pts.)
4. What is the maximum channel capacity ? When does it happen? (0.2 pts.)
5. What are the pros and cons of BEC compared to BSC? Let's assume is channel noise. (0.2 pts.)
Problem 3.b Binary Error and Erasure Channel
Problem 3.c Binary Cascade Channel