Source coding

A First Look at Shannon's Communication Theory

Figure 1: A general communication system.

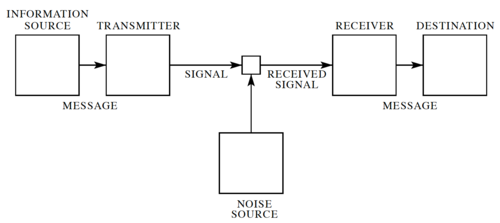
In his landmark 1948 paper, Claude Shannon developed a general model for communication systems, as well as a framework for analyzing these systems. The model has three components: (1) the sender or source, (2) the channel, and (3) the receiver or sink. The model also includes the transmitter that encodes the message into a signal, the receiver, for decoding the signal back into a message, as well the noise of the channel, as shown in Fig. 1.

In Shannon's discrete model, the source provides a stream of symbols from a finite alphabet, ${\mathcal {X}}=\{x_{1},x_{2},\ldots ,x_{n}\}$, which are then encoded. The code is sent through the channel, which could be corrupted by noise, and when the code reaches the other end, it is decoded by the receiver, and then the sink extracts information from the steam of symbols.

Note that sending information in space, e.g. from here to there is equivalent sending information in time, e.g. from now to then. Thus, Shannon's theory applies to both information transmission and information storage.

Source codes

Simply put, a source code ${\mathcal {C}}$ is a mapping from an input alphabet ${\mathcal {X}}$ to another alphabet ${\mathcal {D}}$, which is the set of codewords. If we let $D=|{\mathcal {D}}|$, then we can say that ${\mathcal {C}}$ is a D-ary code. A source code ${\mathcal {C}}$ can be extended so that sequences of symbols drawn from ${\mathcal {X}}$ are encoded as the concatenation of the individual encodings of each source symbol. For example, consider the source alphabet ${\mathcal {X}}=\{1,2,3,4\}$ and the source code

$x$	1	2	3	4
${\mathcal {C}}(x)$	0	010	01	10

will have an extension ${\mathcal {C}}^{*}$ which will map the sequence $2,1,3$ to 010001.

The given definition, by itself, is so general that it may include codes that barely have any practical use. For example, from the definition it is possible to have a code which maps every symbol to 0. You should see that such a code is useless since there is no way to recover the original symbols from a stream of zeros. A code ${\mathcal {C}}$, such as the example just now, is called singular if there exists distinct symbols $x_{1},x_{2}\in {\mathcal {X}}$ such that ${\mathcal {C}}(x_{1})={\mathcal {C}}(x_{2})$. Whenever a code ${\mathcal {C}}$ produces a one-to-one mapping between ${\mathcal {X}}$ and ${\mathcal {D}}$, we will call such a code nonsingular.

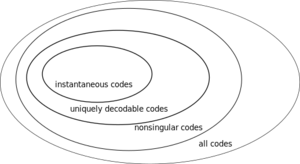
As a preview, below is a list of increasingly stricter classes of source codes:

• nonsingular: if ${\mathcal {C}}(x_{1})\neq {\mathcal {C}}(x_{2})$ whenever $x_{1}\neq x_{2}$.
• uniquely encodable: if the extension ${\mathcal {C}}^{*}$ of ${\mathcal {C}}$ is nonsingular.
• instantaneous: if no codeword is a prefix of another codeword.

Uniquely encodable codes produces encodings that can only correspond to a unique sequence of input symbols. The code presented above is nonsingular, but not uniquely encodable because the encoding 0100 can be obtained from either $(2,1)$ or $(3,1,1)$.

$X$	singular	nonsingular but not uniquely encodable	uniquely encodable but not instantaneous	instantaneous
1	0	0	10	0
2	0	010	00	10
3	0	01	11	110
4	0	10	110	111