Difference between revisions of "2S2122 Activity 3.1"
Ryan Antonio (talk | contribs) |
Ryan Antonio (talk | contribs) |
||
| (10 intermediate revisions by the same user not shown) | |||
| Line 94: | Line 94: | ||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| − | ! scope="col"| Information | + | ! scope="col"| Information Term |
! scope="col"| Function | ! scope="col"| Function | ||
|- | |- | ||
| Line 159: | Line 159: | ||
| style="text-align:center;" | | | style="text-align:center;" | | ||
|- | |- | ||
| − | | style="text-align:center;" | <math> I(r=* | + | | style="text-align:center;" | <math> I(r=*,s=0) </math> |
| style="text-align:center;" | | | style="text-align:center;" | | ||
|- | |- | ||
| − | | style="text-align:center;" | <math> I(r=* | + | | style="text-align:center;" | <math> I(r=*,s=1) </math> |
| style="text-align:center;" | | | style="text-align:center;" | | ||
|- | |- | ||
| Line 228: | Line 228: | ||
[[File:Bsc cascade.PNG|frame|center|Binary Cascade Channel (BCC)]] | [[File:Bsc cascade.PNG|frame|center|Binary Cascade Channel (BCC)]] | ||
| − | A BCC works like an intervening transmitter in between. Think like repeaters for routers. The source sends messages first to the first receiver. Then, the first receiver sends the same message to the second receiver. Assume that the source and the second receiver | + | A BCC works like an intervening transmitter in between. Think like repeaters for routers. The source sends messages first to the first receiver. Then, the first receiver sends the same message to the second receiver. Assume that the source and the second receiver are independent of each other. Determine the following: |
1. Fill up the table below but show your solutions. Solve for each probability first then summarize your results in the table. Answers should be in terms of <math> p </math>, <math> \epsilon_1</math>, and <math> \epsilon_2 </math> only. You may use <math>q = p + \epsilon_1 - 2\epsilon_1 p </math> to keep equations shorter. (0.5 pts. each term) | 1. Fill up the table below but show your solutions. Solve for each probability first then summarize your results in the table. Answers should be in terms of <math> p </math>, <math> \epsilon_1</math>, and <math> \epsilon_2 </math> only. You may use <math>q = p + \epsilon_1 - 2\epsilon_1 p </math> to keep equations shorter. (0.5 pts. each term) | ||
| Line 237: | Line 237: | ||
! scope="col"| Function | ! scope="col"| Function | ||
|- | |- | ||
| − | | style="text-align:center;" | <math> P( | + | | style="text-align:center;" | <math> P(r_2=0) </math> |
| style="text-align:center;" | | | style="text-align:center;" | | ||
|- | |- | ||
| − | | style="text-align:center;" | <math> P( | + | | style="text-align:center;" | <math> P(r_2=1) </math> |
| style="text-align:center;" | | | style="text-align:center;" | | ||
|- | |- | ||
|} | |} | ||
| − | 2. Determine the following measures of information. Fill up the table below but show your solutions. Answers should be in terms of <math> p </math>, <math> \epsilon_1</math>, and <math> \epsilon_2 </math> only. '''Answers should be programming friendly '''. You may use <math>q = p + \epsilon_1 - 2\epsilon_1 p </math> to keep equations shorter. Not following instructions results in -0.05 pts | + | 2. Determine the following measures of information. Fill up the table below but show your solutions. Answers should be in terms of <math> p </math>, <math> \epsilon_1</math>, and <math> \epsilon_2 </math> only. '''Answers should be programming friendly '''. You may use <math>q = p + \epsilon_1 - 2\epsilon_1 p </math> to keep equations shorter. Not following instructions results in -0.05 pts.(0.5 pts. each term) |
{| class="wikitable" | {| class="wikitable" | ||
| Line 255: | Line 255: | ||
| style="text-align:center;" | | | style="text-align:center;" | | ||
|- | |- | ||
| − | | style="text-align:center;" | <math> I(R_1 | + | | style="text-align:center;" | <math> I(R_2,R_1) </math> |
| style="text-align:center;" | | | style="text-align:center;" | | ||
|- | |- | ||
| Line 262: | Line 262: | ||
3. Let's do some analysis, what would <math> I(R_1,S) </math> be if <math> p = 0.5 </math> and <math> \epsilon_1 = 0 </math>? Explain thoroughly how you came up with your answer. (1 pt.) | 3. Let's do some analysis, what would <math> I(R_1,S) </math> be if <math> p = 0.5 </math> and <math> \epsilon_1 = 0 </math>? Explain thoroughly how you came up with your answer. (1 pt.) | ||
| − | 4. Follow up from 3, what is | + | 4. Follow up from 3, what is the appropriate equality/inequality for <math> I(R_1,S) \overset{?}{=} I(R_2,R_1) </math> if <math> 0 < \epsilon_2 < 1 </math> and <math> \epsilon_2 \neq 0.5 </math>? Explain thoroughly how you came up with your answer. Use deductive reasoning. (1 pt.) |
| − | 5. Follow up from 4, what is | + | 5. Follow up from 4, what is the appropriate equality/inequality for <math> I(R_1,S) \overset{?}{=} I(R_2,R_1) </math> if <math> 0 < \epsilon_1 < 1 </math> and <math> \epsilon_1 \neq 0.5 </math>? Explain thoroughly how you came up with your answer. Use deductive reasoning.(1 pt.) |
| − | 6. In general, what is the appropriate equality for <math> I(R_1,S) \overset{?}{=} I(R_2,R_1) </math>? Explain thoroughly how you came up with your answer. (1 pt.) | + | 6. In general, what is the appropriate equality/inequality for <math> I(R_1,S) \overset{?}{=} I(R_2,R_1) </math>? Explain thoroughly how you came up with your answer. Use deductive reasoning.(1 pt.) |
(Big hint: "data processing") | (Big hint: "data processing") | ||
| − | == Huffman Coding (6 pts.) == | + | == Problem 4 - Huffman Coding (6 pts.) == |
The table below shows the source symbols to be sent over a noiseless BSC. | The table below shows the source symbols to be sent over a noiseless BSC. | ||
Latest revision as of 13:10, 6 April 2022
Contents
Instructions
- Answer the following problems individually and truthfully.
- Be sure to show your solutions and please box your final answers.
- Please write your complete name, student number, and section on the upper left corner of your answer sheet. No name, student number, and section, no grade.
- Save your answers in pdf file type with the filename format "section_lastname_firstname_studentnumber.pdf" all in small caps. For example: "abc_wayne_bruce_201101474.pdf".
- Submit your files in the respective submission bin in UVLE. Be sure to submit in the correct class!
- Have fun doing these exercises :) these are not boring!
- You only have two weeks to work on the activities. We will post the hard deadline on UVLE.
- You might want to create your own programs that calculate information and entropy.
Grading Rubrics
- If you have a good solution and a correct answer, you get full points.
- If you have a good solution but the answer is not boxed (or highlighted), you get a 5% deduction of the total points for that problem.
- If you have a good solution but the answer is wrong, you get a 20% deduction of the total points for that problem.
- If your solution is somewhat OK but incomplete. You only get 40% of the total problem.
- If you have a bad solution but with a correct answer. That sounds suspicious. You get 0% for that problem. A bad solution may be:
- You just wrote the given.
- You just dumped equations but no explanation to where they are used.
- You attempted to put a messy flow to distract us. That's definitely bad.
- No attempt at all means no points at all.
- Some problems here may be too long to write. You are allowed to write the general equation instead but be sure to indicate what it means.
- Make sure that you use bits as our units of information.
Problem 1 - The Complete Channel Model (2 pts.)
Answer comprehensively and do the following:
1. Draw the complete channel model. (0.2 pts)
2. What is the source? (0.2 pts)
3. What is the channel? (0.2 pts)
4. What is the receiver? (0.2 pts)
5. What are the encoder and decoder? (0.2 pts)
6. What are codebooks? (0.2 pts)
7. What is coding efficiency? (0.2 pts)
8. What is the maximum capacity of a channel? (0.4 pts)
9. What are symbol rates? (0.4 pts)
10. Where is Waldo? (if we like your answer you get 0.2 pts extra)
Problem 2 - Review of BSC (2 pts.)
1. Draw the BSC channel with correct annotations of important parameters and . (0.1 pts)
2. Fill up the probability table in terms of the important parameters: (0.1 pts each entry)
| Probability Term | Function |
|---|---|
3. Fill up the table below with the measures of information. Answer only in terms of and parameters (and of course constants). When necessary you can use "let be ...". Also, answer with equations that are programming friendly. Answering the simplified version merits half points for that part. (0.1 pts per term)
| Information Term | Function |
|---|---|
4. Explain why when regardless of varying the source probability distribution . (0.2 pts.)
5. Explain what does negative mutual information mean and when can it happen? (0.2 pts.)
6. Explain why means information from the receiver can short-circuit back to the source. (0.1 pts.)
Problem 3 - CRAZY Channels
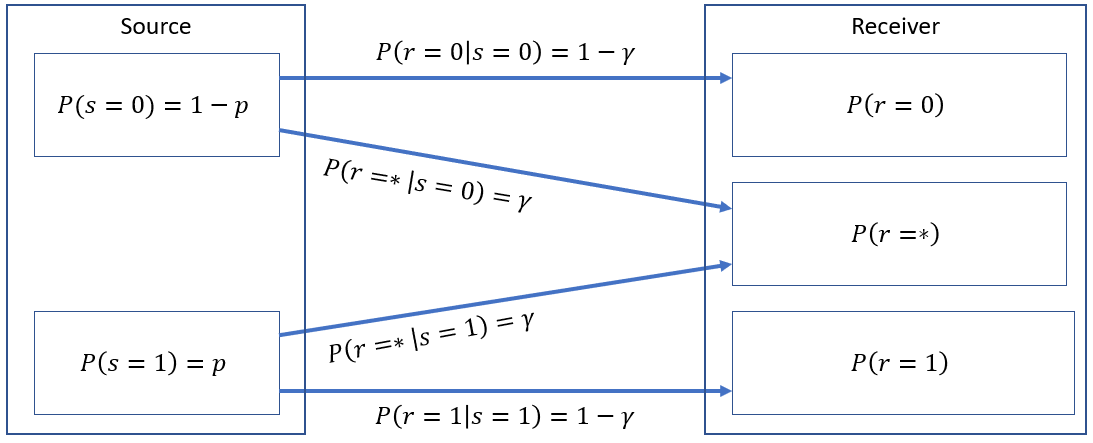
Problem 3.a Binary Erasure Channel (2 pts.)
A Binary Erasure Channel (BEC) is shown below:
BEC is an interesting channel because it has 3 different outputs. The received values , , and . This channel assumes that we can erase or throw unwanted values into the trash bin. It's worth investigating! 😁 Show your complete solutions and box your final answers.
1. Fill up the table below but show your solutions. Solve for each probability first then summarize your results in the table. Answers should be in terms of and only. (0.2 pts. each term)
| Probability Term | Function |
|---|---|
2. Determine the mutual information on a per outcome basis. Fill up the table below but show your solutions. Answers should be in terms of and only. Answers should be in 1 term only . Not following instructions results in -0.05 pts.(0.2 pts. each term)
| Information Term | Function |
|---|---|
3. What is the average mutual information ? (0.2 pts.)
4. What is the maximum channel capacity ? When does it happen? (0.2 pts.)
5. What are the pros and cons of BEC compared to BSC? Let's assume is channel noise. (0.2 pts.)
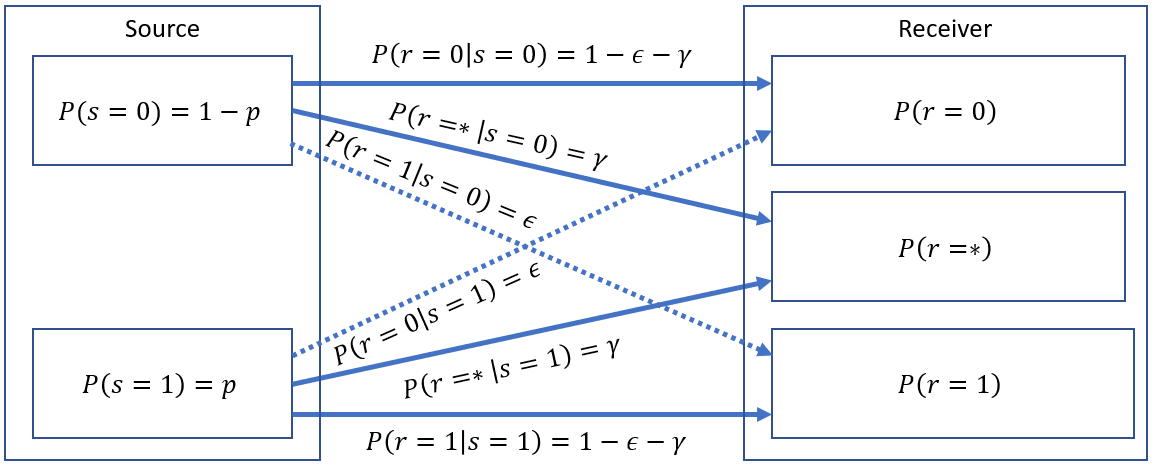
Problem 3.b Binary Error and Erasure Channel (2 pts.)
Below is a Binary Error and Erasure Channel (BEEC) . It's a direct combination of BSC and BEC. Have fun 🐔
This channel is pretty much the same. The only difference is that bit flips are now accounted for. Just in case the erasure decoder is not perfect.
1. Fill up the table below but show your solutions. Solve for each probability first then summarize your results in the table. Answers should be in terms of , , and only. (0.2 pts. each term)
| Probability Term | Function |
|---|---|
2. Determine the following measures of information. Fill up the table below but show your solutions. Answers should be in terms of , , and only. Answers should be programming friendly . Not following instructions results in -0.05 pts.(0.3 pts. each term). You can write "let be ... something" if necessary.
| Information Term | Function |
|---|---|
3. Based on your answers in 3b.2, analyze and interpret, what does an erasure channel do with noise? (0.2 pts.)
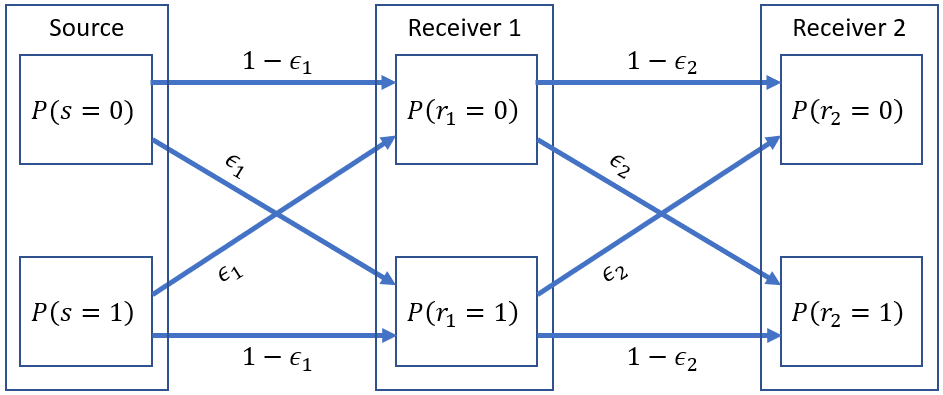
Problem 3.c Binary Cascade Channel (6 pts.)
The figure below shows a Binary Cascade Channel (BCC).
A BCC works like an intervening transmitter in between. Think like repeaters for routers. The source sends messages first to the first receiver. Then, the first receiver sends the same message to the second receiver. Assume that the source and the second receiver are independent of each other. Determine the following:
1. Fill up the table below but show your solutions. Solve for each probability first then summarize your results in the table. Answers should be in terms of , , and only. You may use to keep equations shorter. (0.5 pts. each term)
| Probability Term | Function |
|---|---|
2. Determine the following measures of information. Fill up the table below but show your solutions. Answers should be in terms of , , and only. Answers should be programming friendly . You may use to keep equations shorter. Not following instructions results in -0.05 pts.(0.5 pts. each term)
| Information Term | Function |
|---|---|
3. Let's do some analysis, what would be if and ? Explain thoroughly how you came up with your answer. (1 pt.)
4. Follow up from 3, what is the appropriate equality/inequality for if and ? Explain thoroughly how you came up with your answer. Use deductive reasoning. (1 pt.)
5. Follow up from 4, what is the appropriate equality/inequality for if and ? Explain thoroughly how you came up with your answer. Use deductive reasoning.(1 pt.)
6. In general, what is the appropriate equality/inequality for ? Explain thoroughly how you came up with your answer. Use deductive reasoning.(1 pt.)
(Big hint: "data processing")
Problem 4 - Huffman Coding (6 pts.)
The table below shows the source symbols to be sent over a noiseless BSC.
| Source Symbol | Probability |
|---|---|
| b | 0.15 |
| d | 0.25 |
| g | 0.02 |
| j | 0.10 |
| o | 0.28 |
| space | 0.20 |
Determine the following. Show your complete solution and box your final answers.
1. Draw the final Huffman coding tree. Make sure that you follow the same algorithm from the discussions. (3 pts.) These include:
- All left arrows are tagged as 0s while all right are tagged as 1s.
- When nodes with same probabilities occur, make sure the deepest tree takes the left path.
2. Provide the codebook for the source. (0.5 pts.)
3. Calculate . (0.5 pts.)
4. Calculate . (0.5 pts.)
5. Calculate .(0.5 pts.)
6. Calculate . (0.5 pts.)
7. Decode the message 100011110100100111101. (0.5 pts.)