Difference between revisions of "Coding teaser: source coding"
Ryan Antonio (talk | contribs) |
Ryan Antonio (talk | contribs) |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 3: | Line 3: | ||
==Complete Channel Model== | ==Complete Channel Model== | ||
| − | Previously, we showed a simple channel model that consists of the source, channel, and receiver. In modern communication systems, we | + | Previously, we showed a simple channel model that consists of the source, channel, and receiver. In modern communication systems, we add an '''encoder''' after the source and a '''decoder''' before the receiver. Figure 1 shows the complete channel model. The encoder is used to transform the source symbols into a code that suitable for the channel. The receiver decodes the received message coming out of the channel. |
[[File:Complete channel model.PNG|frame|center|Figure 1: Complete channel model with the encoder added after the source and the decoder added before the receiver.]] | [[File:Complete channel model.PNG|frame|center|Figure 1: Complete channel model with the encoder added after the source and the decoder added before the receiver.]] | ||
| Line 14: | Line 14: | ||
* The binary set <math> \{0,1\} </math> are the '''code symbols'''. | * The binary set <math> \{0,1\} </math> are the '''code symbols'''. | ||
| − | * The encoded patterns <math> \{000,001,010,011,100,101,110,111\} </math> are called the '''codewords'''. For example, <math> 000 </math> is the codeword for the symbol <math> TTT </math>. <math> 101 </math> is the codeword for <math> HTH </math>. In practice, we let some random variable <math> X </math> | + | * The encoded patterns <math> \{000,001,010,011,100,101,110,111\} </math> are called the '''codewords'''. For example, <math> 000 </math> is the codeword for the symbol <math> TTT </math>. <math> 101 </math> is the codeword for <math> HTH </math>. In practice, we let some random variable <math> X </math> have codewords as outcomes <math>\{x_1,x_2,x_3,...,x_n\}</math> associated with probabilities <math> \{P(x_1),P(x_2),P(x_3),...,P(x_n)\} </math>. For example, <math> x_1 = 000 </math> is the codeword for <math> TTT </math>. Moreover, from our example, the source symbols are equiprobable and we have a direct mapping from source symbol to codeword (i.e., <math> s_i \rightarrow x_i </math> ) then it follows that the codewords are equiprobable too: <math> P(x_1)=P(x_2)=P(x_3)=P(x_4)=P(x_5)=P(x_6)=P(x_7)=P(x_8)=\frac{1}{8} </math>. The probability distribution of <math> X </math> can change depending on the encoding scheme. |
* We usually tabulate the encoding or mapping. We call this table the '''codebook'''. It's a simple '''look-up-table (LUT)'''. Let's call the table below as codebook-1. | * We usually tabulate the encoding or mapping. We call this table the '''codebook'''. It's a simple '''look-up-table (LUT)'''. Let's call the table below as codebook-1. | ||
| + | |||
| + | '''Codebook-1''' | ||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| Line 48: | Line 50: | ||
|} | |} | ||
| − | The encoder looks at this table and | + | The encoder looks at this table and encodes message before it gets into the channel. For example, suppose we want to send the message <math> TTTHHHTHTHTH </math>. The encoder uses codebook-1 to translate the source message into an encoded message: <math> 000111010101 </math>. Receivers should also know the same codebook-1 so that they can decode the message. For example, if the encoded message is <math> 101011001110 </math>, then we can decode the message as <math> HTHTHHTTHHHT </math>. Choosing the encoding where the <math> T \rightarrow 0</math> and <math> H \rightarrow 1 </math> is simple. This encoding is arbitrary and it seems convenient for our needs. However, nothing stops us from encoding the source symbols with a different representation. For example, we can choose an encoding where <math> T \rightarrow 1</math> and <math> H \rightarrow 0 </math>. We can go for more complex ones like codebook-2 as shown below: |
| + | |||
| + | '''Codebook-2''' | ||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| Line 81: | Line 85: | ||
|} | |} | ||
| − | Where a source message <math> TTTHHHTHTHTH </math> translates into <math> 0100000000100010000001 </math>. Codebook-2 can also decode an encoded message. For example, when we receive <math> 00000010000100100000001 </math> we get <math> HTHTHHTTHHHT </math>. The choice of the encoding process is purely arbitrary. | + | Where a source message <math> TTTHHHTHTHTH </math> translates into <math> 0100000000100010000001 </math>. Codebook-2 can also decode an encoded message. For example, when we receive <math> 00000010000100100000001 </math> we get <math> HTHTHHTTHHHT </math>. The choice of the encoding process is purely arbitrary. The question you might ask, is the coding scheme efficient?. One metric is the average code length defined as: |
{{NumBlk|::|<math> L(X) = \sum_{i=1}^n P(x_i) l_i </math>|{{EquationRef|1}}}} | {{NumBlk|::|<math> L(X) = \sum_{i=1}^n P(x_i) l_i </math>|{{EquationRef|1}}}} | ||
| Line 93: | Line 97: | ||
<math> L(X) = \frac{1}{8}\cdot 2 + \frac{1}{8}\cdot 3 + \frac{1}{8}\cdot 4 + \frac{1}{8}\cdot 5 + \frac{1}{8}\cdot 6 + \frac{1}{8}\cdot 7 + \frac{1}{8}\cdot 8 + \frac{1}{8}\cdot 9 = 5.5 </math> | <math> L(X) = \frac{1}{8}\cdot 2 + \frac{1}{8}\cdot 3 + \frac{1}{8}\cdot 4 + \frac{1}{8}\cdot 5 + \frac{1}{8}\cdot 6 + \frac{1}{8}\cdot 7 + \frac{1}{8}\cdot 8 + \frac{1}{8}\cdot 9 = 5.5 </math> | ||
| − | Clearly, codebook-1 has a shorter | + | Clearly, codebook-1 has a shorter code length than codebook-2. Let's introduce another metric called the '''coding efficiency'''. Coding efficiency is defined as: |
{{NumBlk|::|<math> \eta = \frac{H(S)}{L(X)} </math>|{{EquationRef|2}}}} | {{NumBlk|::|<math> \eta = \frac{H(S)}{L(X)} </math>|{{EquationRef|2}}}} | ||
| − | Where <math> H(S) </math> is the source entropy. The coding efficiency <math> \eta </math> has a range of <math> 0 \leq \eta \leq 1 </math>. If you recall our "go-to" interpretation of entropy, given some entropy <math> H(S) </math> means we can represent <math> m = 2^{H(S)} </math> outcomes. Essentially, <math> H(S) </math> is the minimum number of bits we can use to represent all outcomes of a source regardless of its distribution. Of course, a smaller coding length is desirable if we want to compress representations. For our simple coin flip example, <math> H(S) = 3 </math>. The efficiency of codebook-1 is <math> \eta = \frac{3}{3} = 1 </math>. Codebook-1 is said to be maximally efficient because it matches the minimum number of bits to represent the source symbols. The efficiency of codebook-2 is <math> \eta = \frac{3}{5.5} = 0.5455 </math>. | + | Where <math> H(S) </math> is the source entropy. The coding efficiency <math> \eta </math> has a range of <math> 0 \leq \eta \leq 1 </math>. If you recall our "go-to" interpretation of entropy, given some entropy <math> H(S) </math> means we can represent <math> m = 2^{H(S)} </math> outcomes. Essentially, <math> H(S) </math> is the minimum number of bits we can use to represent all outcomes of a source regardless of its distribution. Of course, a smaller coding length is desirable if we want to compress representations. For our simple coin flip example, <math> H(S) = 3 </math>. The efficiency of codebook-1 is <math> \eta = \frac{3}{3} = 1 </math>. Codebook-1 is said to be '''maximally efficient''' because it matches the minimum number of bits to represent the source symbols. The efficiency of codebook-2 is <math> \eta = \frac{3}{5.5} = 0.5455 </math>. |
| − | {{Note| <math> L(X) </math> should never be lower than <math> H(S) </math>. Otherwise, that doesn't make sense. How can you represent <math> H(S) = 3 </math> with <math> L(X) = 2 </math>? Something's wrong with your codebook if this happens. |reminder}} | + | {{Note| <math> L(X) </math> should never be lower than <math> H(S) </math>. Otherwise, that doesn't make sense. How can you represent a data set that has <math> H(S) = 3 </math> with <math> L(X) = 2 </math>? Something's wrong with your codebook if this happens. |reminder}} |
==Channel Rates and Channel Capacity== | ==Channel Rates and Channel Capacity== | ||
| − | Let's bring back Bob and Alice into the scene again. When Bob sends his file to Alice, it takes a while before she gets the entire message because the channel has limited bandwidth. Bandwidth is the data rate that the channel supports. Let's define <math> C </math> as the '''maximum channel capacity''' in units of bits per second (bits/s). We'll provide a quantitative approach later. Channels have different rates because of their physical limitations and noise. For example, an ethernet bandwidth can achieve a bandwidth of 10 Gbps (gigabits per second), while Wifi can only achieve at a maximum of 6.9 Gbps. It | + | Let's bring back Bob and Alice into the scene again. When Bob sends his file to Alice, it takes a while before she gets the entire message because the channel has limited bandwidth. Bandwidth is the data rate that the channel supports. Let's define <math> C </math> as the '''maximum channel capacity''' in units of bits per second (bits/s). We'll provide a quantitative approach later. Channels have different rates because of their physical limitations and noise. For example, an ethernet bandwidth can achieve a bandwidth of 10 Gbps (gigabits per second), while Wifi can only achieve at a maximum of 6.9 Gbps. It is slower to communicate wirelessly. It is possible to transmit data to the channel at a much slower rate such that we are not utilizing the full capacity of the channel. We'd like to encode our source symbols into codewords that utilizes the full capacity of a channel. Shannon's source coding theorem says: |
| Line 109: | Line 113: | ||
| − | Take note that, <math> \epsilon </math> in Shannon's statement is not the noise probability that we know. It's just a term that is used to indicate a small margin of error. In a nutshell, Shannon's source coding theorem says that we can calculate a maximum symbol rate (symbols/s) that utilizes the maximum channel rate <math>C </math> while knowing the source entropy <math> H(S) </math>. | + | Take note that, <math> \epsilon </math> in Shannon's statement is not the noise probability that we know. It's just a term that is used to indicate a small margin of error. In a nutshell, Shannon's source coding theorem says that we can calculate a maximum symbol rate (symbols/s) that utilizes the maximum channel rate <math>C </math> while knowing the source entropy <math> H(S) </math>. Then, knowing this maximum symbol rate, we can find an encoding scheme that can get us close to this ideal rate. The maximum symbol rate is given by: |
{{NumBlk|::|<math> R_{\textrm{max}} = \frac{C}{H(S)} </math>|{{EquationRef|3}}}} | {{NumBlk|::|<math> R_{\textrm{max}} = \frac{C}{H(S)} </math>|{{EquationRef|3}}}} | ||
| Line 117: | Line 121: | ||
=== Channel Rate Example 1: Three Coin Flips === | === Channel Rate Example 1: Three Coin Flips === | ||
| − | Let's re-use the three coin flips example again. Suppose we want to send the three coin flip symbols over some channel that has a channel capacity <math> C = 3</math> bits/s. We also know (from the above example) that we need a minimum of <math> H(S) = 3</math> bits per symbol to represent each outcome. This translates to: | + | Let's re-use the three coin flips example again. Suppose we want to send the three coin flip symbols over some channel that has a channel capacity <math> C = 3</math> bits/s (let's just say this is a given). We also know (from the above example) that we need a minimum of <math> H(S) = 3</math> bits per symbol to represent each outcome. This translates to: |
<math> R_{\textrm{max}} = \frac{3 \ \textrm{bits/s}}{ 3 \ \textrm{bits/symbols}} = 1 \ \textrm{symbols/s} </math> | <math> R_{\textrm{max}} = \frac{3 \ \textrm{bits/s}}{ 3 \ \textrm{bits/symbols}} = 1 \ \textrm{symbols/s} </math> | ||
| − | If we are to utilize the maximum capacity of the channel, we need to encode the source symbols <math> \{TTT,TTH,THT,THH,HTT,HTH,HHT,HHH\} </math> to its binary representation such that each binary digit in each codeword <math> x_i </math> provides 1 bit of information <ref> Stone, J.V. , ''Information Theory: A Tutorial Introduction'', Sebtel Press, 2015. </ref>. Luckily, codebook-1 does this because we have a coding efficiency of <math> \eta = 1 </math> | + | If we are to utilize the maximum capacity of the channel, we need to encode the source symbols <math> \{TTT,TTH,THT,THH,HTT,HTH,HHT,HHH\} </math> to its binary representation such that each binary digit in each codeword <math> x_i </math> provides 1 bit of information <ref> Stone, J.V. , ''Information Theory: A Tutorial Introduction'', Sebtel Press, 2015. </ref>. Luckily, codebook-1 does this because we have a coding efficiency of <math> \eta = 1 </math>. This result means that every binary digit of the codeword provides at least 1-bit of information. We are maximally efficient with this encoding. If you think about it, if we send 1 symbol/s to the channel and our encoding has 1 symbol (e.g., TTT) is 3 bits long then essentially we are able to send 3 bits/s to the channel. Since <math> C = 3 </math> bits/s, then we are utilizing the entire maximum channel capacity. |
{{Note| From the above example, can we actually go beyond <math> R_{\textrm{max}} = \frac{C}{H(S)} </math> symbols/s? NO. Shannon explicitly said that "It is not possible to transmit at an average rate greater than <math> C/H </math>." This is the maximum symbol rate already. |reminder}} | {{Note| From the above example, can we actually go beyond <math> R_{\textrm{max}} = \frac{C}{H(S)} </math> symbols/s? NO. Shannon explicitly said that "It is not possible to transmit at an average rate greater than <math> C/H </math>." This is the maximum symbol rate already. |reminder}} | ||
| Line 127: | Line 131: | ||
=== Channel Rate Example 2: A 6-sided Die=== | === Channel Rate Example 2: A 6-sided Die=== | ||
| − | This time, suppose we want to send the symbols of a fair 6-sided die on a channel that only has <math> C = 1 </math> bits/s. Such that <math> S </math> has outcomes <math> \{1,2,3,4,5,6 \} </math>. Of course, all outcomes are equiprobable with <math> P(s_i) = \frac{1}{6} </math>. From here, we can determined <math> H(S) = \log_2(6) = 2.58 </math> bits/symbol. Therefore: | + | This time, suppose we want to send the symbols of a fair 6-sided die on a channel that only has <math> C = 1 </math> bits/s (this is a separate given). Such that <math> S </math> has outcomes <math> \{1,2,3,4,5,6 \} </math>. Of course, all outcomes are equiprobable with <math> P(s_i) = \frac{1}{6} </math>. From here, we can determined <math> H(S) = \log_2(6) = 2.58 </math> bits/symbol. Therefore: |
| − | |||
| − | + | <math> R_{\textrm{max}} = \frac{1 \ \textrm{bits/s}}{ 2.58 \ \textrm{bits/symbols}} = 0.387 </math> symbols/s | |
| + | |||
| + | Again, Shannon says that with a given <math> C </math> and <math> H(S) </math> we can only transmit at a maximum symbol rate of <math> R_{\textrm{max}} </math> symbols/s. Now, let's think of an encoding scheme that suits our needs. For convenience, to represent 6 unique outcomes, we can use 3 bits to represent each outcome. Let's say we have codebook-3: | ||
| + | |||
| + | |||
| + | '''Codebook-3''' | ||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| Line 158: | Line 166: | ||
|} | |} | ||
| − | The coding efficiency | + | The coding efficiency of codebook-3 used for the 6-die example is: |
| + | |||
<math> \eta = \frac{H(S)}{L(X)} = \frac{2.58}{3} = 0.86 </math> | <math> \eta = \frac{H(S)}{L(X)} = \frac{2.58}{3} = 0.86 </math> | ||
| − | + | ||
| + | Codebook-3 is not that efficient but it will suffice for now. Here, let's introduce the '''effective symbol rate''' <math> R_X </math> due to the new encoding: | ||
| + | |||
{{NumBlk|::|<math> R_{X} = \frac{\eta C}{H(S)} </math>|{{EquationRef|4}}}} | {{NumBlk|::|<math> R_{X} = \frac{\eta C}{H(S)} </math>|{{EquationRef|4}}}} | ||
| − | Our encoding scheme affects how much data we're putting into the channel. If our coding efficiency isn't optimal <math> \eta \neq 1</math> then we are only utilizing a fraction of the maximum capacity <math> C</math>. Hence we | + | |
| + | Our encoding scheme affects how much data we're putting into the channel. If our coding efficiency isn't optimal <math> \eta \neq 1</math> then we are only utilizing a fraction of the maximum capacity <math> C</math>. Hence we have the effective channel transmission rate <math> \eta C </math> incorporated into our effective symbol rate <math> R_X </math>. Calculating <math> R_X </math> for codebook-3 would give: | ||
| + | |||
<math> R_X = \frac{0.86 \cdot 1}{2.58} = 0.333</math> symbols/s. | <math> R_X = \frac{0.86 \cdot 1}{2.58} = 0.333</math> symbols/s. | ||
| − | |||
| + | Observe that <math> R_X = 0.333 < R_{\textrm{max}} = 0.387 </math>. We are not even close to the maximum rate. Can we find a better encoding? How about this, suppose we create a composite symbol that consists of the three 6-sided die symbols. For example, we can let <math> 111 </math> be one symbol, or we can let <math> 555 </math> be another symbol. If we do so, then we have around <math> 6\times6\times6 = 216 </math> unique possible outcomes for the new set of symbols. To represent 216 outcomes we need a minimum of 8 bits of code length (because <math> 2^8 = 256 </math>). So we can have codebook-4 as: | ||
| + | |||
| + | |||
| + | '''Codebook-4''' | ||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| Line 197: | Line 213: | ||
|} | |} | ||
| − | The underscores are just there to separate the 4 bits for clarity. Codebook-4 looks really long but in practice, | + | The underscores are just there to separate the 4 bits for clarity. Codebook-4 looks really long but in practice, it's still small. So what changes? Since we have 8 bits per 3 symbols, the effective code length per symbol is <math> L(X) = \frac{8}{3} </math>. Take note that all outcomes are equiprobable so dividing the 8 bits by 3 symbols is enough. This results in a coding efficiency of: |
| + | |||
<math> \eta = \frac{H(S)}{L(X)} = \frac{2.58}{2.66} = 0.97 </math> | <math> \eta = \frac{H(S)}{L(X)} = \frac{2.58}{2.66} = 0.97 </math> | ||
| + | |||
Cool! We're much closer to being maximally efficient. Now, let's compute the new <math> R_X </math> for codebook-4: | Cool! We're much closer to being maximally efficient. Now, let's compute the new <math> R_X </math> for codebook-4: | ||
| + | |||
<math> R_X = \frac{\eta C}{H(S)} = \frac{0.97}{2.58} = 0.376 </math> symbols/s. | <math> R_X = \frac{\eta C}{H(S)} = \frac{0.97}{2.58} = 0.376 </math> symbols/s. | ||
| + | |||
Superb! The new <math> R_X = 0.376 </math> is close to the maximum rate of <math> R_{\textrm{max}} = 0.387 </math>. The key trick was to create a composite symbols that consists of 3 of the original source symbols, then represent them with 8 binary digits of codewords. | Superb! The new <math> R_X = 0.376 </math> is close to the maximum rate of <math> R_{\textrm{max}} = 0.387 </math>. The key trick was to create a composite symbols that consists of 3 of the original source symbols, then represent them with 8 binary digits of codewords. | ||
| Line 213: | Line 233: | ||
[[File:Bsc irs sweep.PNG|400px|thumb|right|Figure 2: <math> I(R,S) </math> of a BSC with varying <math> p </math> and parametrizing <math> \epsilon </math>.]] | [[File:Bsc irs sweep.PNG|400px|thumb|right|Figure 2: <math> I(R,S) </math> of a BSC with varying <math> p </math> and parametrizing <math> \epsilon </math>.]] | ||
| − | This time, let's | + | This time, let's study how we can quantitatively determine the maximum channel capacity. In the last module, we comprehensively investigated the measures of <math> H(R) </math>, <math>H(R|S) </math>, and <math> I(R,S) </math> on a BSC. Recall that: |
| Line 219: | Line 239: | ||
| − | If you think about it, <math> I(R,S) </math> is a measure of channel quality. It tells us how much we can estimate the input from an observed output. <math> I(R,S) </math> is a measure of the received information contained in the source information. Ideally if there is no noise, then <math> H(R|S) = 0 </math> resulting in <math> I(R,S) = H(S) = H(R) </math>. We want this because | + | If you think about it, <math> I(R,S) </math> is a measure of channel quality. It tells us how much we can estimate the input from an observed output. <math> I(R,S) </math> is a measure of the received information contained in the source information. Ideally, if there is no noise, then <math> H(R|S) = 0 </math> resulting in <math> I(R,S) = H(S) = H(R) </math>. We want this because all the information from the source gets to the receiver! When noise is present <math> H(R|S) \neq 0 </math>, it degrades the quality of our <math> I(R,S) </math> and the information about the receiver contained in the source is now being shared with noise. This only means one thing: ''' we want <math> I(R,S) </math> to be at maximum'''. From the previous discussion, we presented how <math> I(R,S) </math> varies with <math> p </math> while parametrizing the noise probability <math> \epsilon </math>. Figure 2 shows this plot. We can visualize <math> I(R,S) </math> like a pipe while the noise parameter <math> \epsilon </math> limits the flow of information. Figure 3 GIF shows the pipe visualization. |
[[File:Pipe irs.gif|frame|center|Figure 3: Pipe visualization for <math> I(R,S) </math>]] | [[File:Pipe irs.gif|frame|center|Figure 3: Pipe visualization for <math> I(R,S) </math>]] | ||
| Line 235: | Line 255: | ||
| − | Here, <math> C </math> is in units of bits/s. It tells us the maximum number of data that we can transmit per unit of time. Both <math> H(R) </math> and <math> H(R|S) </math> are affected by noise parameter <math> \epsilon </math>. In a way, noise limits <math> C </math>. For example, a certain <math> \epsilon </math> can only provide a certain maximum <math> I(R,S) </math>. Looking at figure 2, when <math> \epsilon = 0</math> (or <math> \epsilon = 1</math>) we can get a maximum <math> I(R,S) = 1</math> bits/s provided that the probability distribution of the symbols that get into the channel is <math> p = 0.5 </math>. When <math> \epsilon = 0.25</math> (or <math> \epsilon = 0.75 </math>) we can also get a maximum <math>I(R,S) = 0.189 </math> bits/s when <math> p = 0.5 </math>. Let's determine <math> C </math> of a BSC given some <math> p </math> and <math> \epsilon </math>. Since we know <math> H(R) </math> follows the Bernoulli entropy <math> H_b(q) </math> where <math> q = p + \epsilon - 2\epsilon p </math>. Then we can write: | + | Here, <math> C </math> is in units of bits/s. It tells us the maximum number of data that we can transmit per unit of time. Both <math> H(R) </math> and <math> H(R|S) </math> are affected by the noise parameter <math> \epsilon </math>. In a way, noise limits <math> C </math>. For example, a certain <math> \epsilon </math> can only provide a certain maximum <math> I(R,S) </math>. Looking at figure 2, when <math> \epsilon = 0</math> (or <math> \epsilon = 1</math>) we can get a maximum <math> I(R,S) = 1</math> bits/s provided that the probability distribution of the symbols that get into the channel is <math> p = 0.5 </math>. When <math> \epsilon = 0.25</math> (or <math> \epsilon = 0.75 </math>) we can also get a maximum <math>I(R,S) = 0.189 </math> bits/s when <math> p = 0.5 </math>. Let's determine <math> C </math> of a BSC given some <math> p </math> and <math> \epsilon </math>. Since we know <math> H(R) </math> follows the Bernoulli entropy <math> H_b(q) </math> where <math> q = p + \epsilon - 2\epsilon p </math>. Then we can write: |
| Line 241: | Line 261: | ||
| − | <math> \max(H(R)) = 1 </math> bits when <math> q = 0.5 </math>. Since <math> \epsilon </math> is fixed depending on a channel, we can manipulate the input probability <math> p </math> of the symbols that get into the channel such that we can force <math> q = 0.5</math> and achieve the maximum <math> H(R) </math>. | + | <math> \max(H(R)) = 1 </math> bits when <math> q = 0.5 </math>. Since <math> \epsilon </math> is fixed depending on a channel, we can manipulate the input probability <math> p </math> of the source symbols that get into the channel such that we can force <math> q = 0.5</math> and achieve the maximum <math> H(R) </math>. |
| Line 259: | Line 279: | ||
| − | In equation 6, we can assume <math> H_b(q) = 1 </math> because we know we can achieve maximum entropy when we set <math> q = p = 0.5 </math>. Equation 6 shows how the maximum capacity is limited by the noise <math> \epsilon </math>. It describes the pipe visualization in figure 3. When <math> \epsilon = 0</math>, <math> H_b(\epsilon) = 0 </math> and our BSC has <math> C = 1.0 </math> bits/s. When <math> \epsilon = 0.5 </math>, <math> H_b(\epsilon) = 1 </math>, the noise entropy is at maximum and our channel has <math> C = 0 </math> bits/s. Clearly, we can't transmit data this way. Lastly, when <math> \epsilon = 1 </math>, then <math> H_b(\epsilon) = 0 </math> again and we're back to having <math> C = 1</math> bits/s. | + | In equation 6, we can assume <math> \max (H_b(q)) = 1 </math> because we know we can achieve maximum entropy when we set <math> q = p = 0.5 </math>. Equation 6 shows how the maximum capacity is limited by the noise <math> \epsilon </math>. It describes the pipe visualization in figure 3. When <math> \epsilon = 0</math>, <math> H_b(\epsilon) = 0 </math> and our BSC has <math> C = 1.0 </math> bits/s. When <math> \epsilon = 0.5 </math>, <math> H_b(\epsilon) = 1 </math>, the noise entropy is at maximum and our channel has <math> C = 0 </math> bits/s. Clearly, we can't transmit data this way. Lastly, when <math> \epsilon = 1 </math>, then <math> H_b(\epsilon) = 0 </math> again and we're back to having <math> C = 1</math> bits/s. |
The most important concept in determining maximum channel capacity is to use equation 5 for any channel model. Moreover, from our simple BSC derivation, we can see that in order to maximize the effective channel capacity, we need to encode our source symbols into codewords such that <math> p \rightarrow 0.5 </math> before it gets sent over the channel. This is the essence of the concept '''source coding''' where we encode the source to achieve maximum entropy. This is related to equation 4 where <math> \eta C</math> tells us the effective channel rate assuming we have not encoded our source symbols to achieve <math> p = 0.5 </math>. If we have successfully achieved <math> p =0.5 </math> for the encoded codewords, then on average we utilize the maximum capacity <math> C </math> (i.e., <math> \eta = 1</math>). | The most important concept in determining maximum channel capacity is to use equation 5 for any channel model. Moreover, from our simple BSC derivation, we can see that in order to maximize the effective channel capacity, we need to encode our source symbols into codewords such that <math> p \rightarrow 0.5 </math> before it gets sent over the channel. This is the essence of the concept '''source coding''' where we encode the source to achieve maximum entropy. This is related to equation 4 where <math> \eta C</math> tells us the effective channel rate assuming we have not encoded our source symbols to achieve <math> p = 0.5 </math>. If we have successfully achieved <math> p =0.5 </math> for the encoded codewords, then on average we utilize the maximum capacity <math> C </math> (i.e., <math> \eta = 1</math>). | ||
| − | {{Note| Don't get mad but despite having rigorous discussions about channels and noise, data compression | + | {{Note| Don't get mad, but despite having rigorous discussions about channels and noise, data compression assumes a '''noiseless channel'''. Phew! So much for going through the hard efforts. |reminder}} |
==Huffman Coding== | ==Huffman Coding== | ||
| − | The first two examples of encoding looked into source symbols that are equiprobable. First, we've shown that if <math> H(S) = L(X) \rightarrow \eta = 1</math>, we can fully utilize the channel capacity. We've seen this in our three flips of a fair coin example. When <math> H(S) < L(X) \rightarrow 0 < \eta < 1</math>, we had to duplicate the source symbols to so that the effective code efficiency <math> \eta \approx 1 </math> and we can get closer to | + | The first two examples of encoding looked into source symbols that are equiprobable. First, we've shown that if <math> H(S) = L(X) \rightarrow \eta = 1</math>, we can fully utilize the channel capacity. We've seen this in our three flips of a fair coin example. When <math> H(S) < L(X) \rightarrow 0 < \eta < 1</math>, we had to duplicate the source symbols to so that the effective code efficiency <math> \eta \approx 1 </math> and we can get closer to fully utilizing the channel. We're seeing a pattern that the closer our coding efficiency is to 1, we get closer to maximizing the channel capacity. However, what happens when the source symbols are not equiprobable? |
Let's say we want to communicate the sum of two fair 6-sided die rolls. Our source alphabet <math> S </math> contains symbols <math>\{2,3,4,5,6,7,8,9,10,11,12 \} </math>. The source probability distribution is shown in the table below: | Let's say we want to communicate the sum of two fair 6-sided die rolls. Our source alphabet <math> S </math> contains symbols <math>\{2,3,4,5,6,7,8,9,10,11,12 \} </math>. The source probability distribution is shown in the table below: | ||
| Line 324: | Line 344: | ||
|} | |} | ||
| − | What would be the best encoding for this source? The source entropy <math> H(S) = 3.27 </math> bits. Let's say codebook-5 is a simple binary representation. Since there are <math> n = 11 </math> outcomes, then using 4 bits for each codeword | + | What would be the best encoding for this source? The source entropy <math> H(S) = 3.27 </math> bits. Let's say codebook-5 is a simple binary representation. Since there are <math> n = 11 </math> outcomes, then using 4 bits for each codeword will suffice. Codebook-5 is shown below: |
| Line 371: | Line 391: | ||
| − | The Huffman coding is a lossless compression. The encoding has this interesting property where frequent symbols map to short codewords, while rare symbols map to long codewords. In fact, Huffman codes | + | The Huffman coding is a lossless compression. The encoding has this interesting property where frequent symbols map to short codewords, while rare symbols map to long codewords. In fact, Huffman codes says that we can have an average code length of <math> L(X) </math> that's within a unit of <math> H(X) </math> then that means we'll have <math> \eta \approx 1 </math>. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
=== Huffman Coding Example 1 === | === Huffman Coding Example 1 === | ||
| Line 416: | Line 430: | ||
3. Repeat step 1 and 2 with the new composite node as part of the list. Do this until we are left with 1 node. | 3. Repeat step 1 and 2 with the new composite node as part of the list. Do this until we are left with 1 node. | ||
| − | * When you reach step 2 and a composite node has the same probability with another node (probably a composite node too), the node with the longer path | + | * When you reach step 2 and a composite node has the same probability with another node (probably a composite node too), the node with the longer path takes the left side. |
4. Write the Huffman codes starting from the top of the tree down to the root of the symbol. | 4. Write the Huffman codes starting from the top of the tree down to the root of the symbol. | ||
| Line 436: | Line 450: | ||
4. We combined <math> b</math> and <math> c </math> to get composite node <math> bc </math> with <math> P(bc) = P(b) + P(c) = 0.62</math>. We need to re-arrange the nodes in ascending order. | 4. We combined <math> b</math> and <math> c </math> to get composite node <math> bc </math> with <math> P(bc) = P(b) + P(c) = 0.62</math>. We need to re-arrange the nodes in ascending order. | ||
| − | 5. We reached the last tree so we just combined the composite nodes <math> aed </math> and <math> bc </math>. We should get <math> P(aedbc) = P(aed) + P(bc) = 1.00 </math> if we did the Huffman code correctly. All left arrows are tagged with 0s while all right arrows are tagged with 1s. We can get the Huffman codes for all symbols from this tree. | + | 5. We reached the last tree so we just combined the composite nodes <math> aed </math> and <math> bc </math>. We should get <math> P(aedbc) = P(aed) + P(bc) = 1.00 </math> if we did the Huffman code correctly. All left arrows are tagged with 0s while all right arrows are tagged with 1s. We can get the Huffman codes for all symbols from this tree. You can actually swap the directions for 1s and 0s, but for our example, all left arrows use 0s while all right arrows use 1s. |
| − | The top of the tree will be the MSB (left-most bit) while the bottom of the tree will be the LSB (right-most bit). For example, to get the Huffman code | + | The top of the tree will be the MSB (left-most bit) while the bottom of the tree will be the LSB (right-most bit). For example, to get the Huffman code for <math> a </math> we have (from the top of the tree) <math> 0 \rightarrow 0 \rightarrow 0 = 000</math>. To get <math> d </math> we have <math> 0 \rightarrow 1 = 01 </math>. Simple right? We can generate a new codebook for our example. |
| Line 465: | Line 479: | ||
|} | |} | ||
| − | The cool part about Huffman coding is that codewords are uniquely decodable. This means that for every codeword, we can immediately tell | + | The cool part about Huffman coding is that codewords are uniquely decodable. This means that for every codeword, we can immediately tell the symbol it's pertaining to. We'll get back to this in the next module. For example, if the we received an encoded message <math> 110010100101000001100111 </math> we can decode it as <math>cededaebdc </math>. We can calculate the average code length for this one. Recall that: |
| Line 471: | Line 485: | ||
| − | Therefore we have: | + | Therefore, we have: |
| Line 477: | Line 491: | ||
| − | If we | + | If we send these encoded symbols across a channel according to the probability distribution of each symbol, we would have <math> L(X) = 2.16 </math> on average. The entropy <math> H(S) </math> is: |
| Line 483: | Line 497: | ||
| − | Therefore the coding efficiency for this example would be <math> \eta = \frac{H(S)}{L(X)} = \frac{2.078}{2.16} = 0.96 </math> which is really close to being maximally efficient. Cool right? If we | + | Therefore the coding efficiency for this example would be <math> \eta = \frac{H(S)}{L(X)} = \frac{2.078}{2.16} = 0.96 </math> which is really close to being maximally efficient. Cool right? If we just represent each outcome with 3 binary digits (because there are 5 outcomes so we need <math> m = 2^3 = 8 </math>), then <math> L(X) = 3 </math> and the coding efficiency for a straight-forward binary coding would be <math> \eta = \frac{H(S)}{L(X)} = \frac{2.078}{3} = 0.69 </math>. Huffman coding rules! |
| Line 543: | Line 557: | ||
|- | |- | ||
| style="text-align:center;" | d | | style="text-align:center;" | d | ||
| − | | style="text-align:center;" | | + | | style="text-align:center;" | 1011 |
|- | |- | ||
| style="text-align:center;" | e | | style="text-align:center;" | e | ||
| − | | style="text-align:center;" | | + | | style="text-align:center;" | 1010 |
|- | |- | ||
|} | |} | ||
| Line 569: | Line 583: | ||
Still a much better coding efficiency that using a direct 3-bit binary representation because <math> \eta = \frac{H(S)}{L(X)} = \frac{2.046}{3} = 0.682 </math>. | Still a much better coding efficiency that using a direct 3-bit binary representation because <math> \eta = \frac{H(S)}{L(X)} = \frac{2.046}{3} = 0.682 </math>. | ||
| + | |||
| + | === Huffman Coding Example 3 === | ||
| + | |||
| + | Going back to our 2-die roll example, we can use Huffman coding to get codebook 6: | ||
| + | |||
| + | |||
| + | '''Codebook-6''' | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! scope="col"| Source Symbol | ||
| + | ! scope="col"| Codeword | ||
| + | |- | ||
| + | | style="text-align:center;" | 2 | ||
| + | | style="text-align:center;" | 00101 | ||
| + | |- | ||
| + | | style="text-align:center;" | 3 | ||
| + | | style="text-align:center;" | 1000 | ||
| + | |- | ||
| + | | style="text-align:center;" | 4 | ||
| + | | style="text-align:center;" | 000 | ||
| + | |- | ||
| + | | style="text-align:center;" | 5 | ||
| + | | style="text-align:center;" | 011 | ||
| + | |- | ||
| + | | style="text-align:center;" | 6 | ||
| + | | style="text-align:center;" | 110 | ||
| + | |- | ||
| + | | style="text-align:center;" | 7 | ||
| + | | style="text-align:center;" | 111 | ||
| + | |- | ||
| + | | style="text-align:center;" | 8 | ||
| + | | style="text-align:center;" | 101 | ||
| + | |- | ||
| + | | style="text-align:center;" | 9 | ||
| + | | style="text-align:center;" | 010 | ||
| + | |- | ||
| + | | style="text-align:center;" | 10 | ||
| + | | style="text-align:center;" | 1001 | ||
| + | |- | ||
| + | | style="text-align:center;" | 11 | ||
| + | | style="text-align:center;" | 0011 | ||
| + | |- | ||
| + | | style="text-align:center;" | 12 | ||
| + | | style="text-align:center;" | 00100 | ||
| + | |- | ||
| + | |} | ||
| + | |||
| + | Codebook-6 is just one table. Sometimes we may swap the direction of arrows. Moreover, sometimes when we end up having components of the same probabilities, we may have swapped them in a different direction. Regardless, the Huffman codes generate a mapping that is uniquely decodable. Codebook-6 has an average code length of <math> L(X) = 3.31 </math>. The two 6-sided die rolls has a source entropy of <math> H(S) = 3.27 </math> bits/s. Therefore <math> \eta = \frac{H(S)}{L(X)} = \frac{3.27}{3.31} = 0.99 </math>. That is superbly close to a maximal coding efficiency. Lastly, if you observe all the Huffman encoding examples, all frequent symbols have shorter code lengths while all rare symbols have longer codelengths. This is a cool data compression algorithm. | ||
| + | |||
| + | == Summary == | ||
| + | |||
| + | For this chapter, we summarize our learnings: | ||
| + | |||
| + | * We covered the complete model for a channel while introducing components like '''encoder''' and '''decoder'''. | ||
| + | * We introduced new definitions: '''code symbols''', '''codewords''', '''codebooks''', '''coding efficiency''', '''maximum channel capacity''', and '''effective channel rates'''. | ||
| + | * We had a sneak peak of the '''source coding''' theorem. | ||
| + | * We derived a quantitative measure of channel capacity for BSC. | ||
| + | * Lastly, we studied the Huffman coding and appreciated how cool it is. | ||
| + | |||
| + | Have fun doing the lab exercises 😃 | ||
==References== | ==References== | ||
Latest revision as of 16:02, 3 March 2022
Contents
Complete Channel Model
Previously, we showed a simple channel model that consists of the source, channel, and receiver. In modern communication systems, we add an encoder after the source and a decoder before the receiver. Figure 1 shows the complete channel model. The encoder is used to transform the source symbols into a code that suitable for the channel. The receiver decodes the received message coming out of the channel.
Let's bring back Bob and Alice into the scene again. This time let's use the complete channel model. Since most of our communication systems use binary representations, Bob needs to encode his data into binary digits before he sends it over the channel.
Let's look at a few examples. Suppose our source alphabet has the symbols of all combinations of flipping three fair coins. Then our symbols would be . Bob needs to map each symbol into a binary representation such that . This is the encoding process. Let's add new definitions:
- The binary set are the code symbols.
- The encoded patterns are called the codewords. For example, is the codeword for the symbol . is the codeword for . In practice, we let some random variable have codewords as outcomes associated with probabilities . For example, is the codeword for . Moreover, from our example, the source symbols are equiprobable and we have a direct mapping from source symbol to codeword (i.e., ) then it follows that the codewords are equiprobable too: . The probability distribution of can change depending on the encoding scheme.
- We usually tabulate the encoding or mapping. We call this table the codebook. It's a simple look-up-table (LUT). Let's call the table below as codebook-1.
Codebook-1
| Source Symbol | Codeword |
|---|---|
| TTT | 000 |
| TTH | 001 |
| THT | 010 |
| THH | 011 |
| HTT | 100 |
| HTH | 101 |
| HHT | 110 |
| HHH | 111 |
The encoder looks at this table and encodes message before it gets into the channel. For example, suppose we want to send the message . The encoder uses codebook-1 to translate the source message into an encoded message: . Receivers should also know the same codebook-1 so that they can decode the message. For example, if the encoded message is , then we can decode the message as . Choosing the encoding where the and is simple. This encoding is arbitrary and it seems convenient for our needs. However, nothing stops us from encoding the source symbols with a different representation. For example, we can choose an encoding where and . We can go for more complex ones like codebook-2 as shown below:
Codebook-2
| Source Symbol | Codeword |
|---|---|
| TTT | 01 |
| TTH | 001 |
| THT | 0001 |
| THH | 00001 |
| HTT | 000001 |
| HTH | 0000001 |
| HHT | 00000001 |
| HHH | 000000001 |
Where a source message translates into . Codebook-2 can also decode an encoded message. For example, when we receive we get . The choice of the encoding process is purely arbitrary. The question you might ask, is the coding scheme efficient?. One metric is the average code length defined as:
-
(1)
-
Where is the code length of the codeword . For example, the average code length of codebook-1 is:
The average code length of codebook-2 is:
Clearly, codebook-1 has a shorter code length than codebook-2. Let's introduce another metric called the coding efficiency. Coding efficiency is defined as:
-
(2)
-
Where is the source entropy. The coding efficiency has a range of . If you recall our "go-to" interpretation of entropy, given some entropy means we can represent outcomes. Essentially, is the minimum number of bits we can use to represent all outcomes of a source regardless of its distribution. Of course, a smaller coding length is desirable if we want to compress representations. For our simple coin flip example, . The efficiency of codebook-1 is . Codebook-1 is said to be maximally efficient because it matches the minimum number of bits to represent the source symbols. The efficiency of codebook-2 is .
Channel Rates and Channel Capacity
Let's bring back Bob and Alice into the scene again. When Bob sends his file to Alice, it takes a while before she gets the entire message because the channel has limited bandwidth. Bandwidth is the data rate that the channel supports. Let's define as the maximum channel capacity in units of bits per second (bits/s). We'll provide a quantitative approach later. Channels have different rates because of their physical limitations and noise. For example, an ethernet bandwidth can achieve a bandwidth of 10 Gbps (gigabits per second), while Wifi can only achieve at a maximum of 6.9 Gbps. It is slower to communicate wirelessly. It is possible to transmit data to the channel at a much slower rate such that we are not utilizing the full capacity of the channel. We'd like to encode our source symbols into codewords that utilizes the full capacity of a channel. Shannon's source coding theorem says:
"Let a source have entropy (bits per symbol) and a channel have a capacity (bits per second). Then it is possible to encode the output of the source in such a way as to transmit at the average rate symbols per second over the channel where is arbitrarily small. It is not possible to transmit at an average rate greater than ." [1]
Take note that, in Shannon's statement is not the noise probability that we know. It's just a term that is used to indicate a small margin of error. In a nutshell, Shannon's source coding theorem says that we can calculate a maximum symbol rate (symbols/s) that utilizes the maximum channel rate while knowing the source entropy . Then, knowing this maximum symbol rate, we can find an encoding scheme that can get us close to this ideal rate. The maximum symbol rate is given by:
-
(3)
-
Let's look at a few examples to appreciate this.
Channel Rate Example 1: Three Coin Flips
Let's re-use the three coin flips example again. Suppose we want to send the three coin flip symbols over some channel that has a channel capacity bits/s (let's just say this is a given). We also know (from the above example) that we need a minimum of bits per symbol to represent each outcome. This translates to:
If we are to utilize the maximum capacity of the channel, we need to encode the source symbols to its binary representation such that each binary digit in each codeword provides 1 bit of information [2]. Luckily, codebook-1 does this because we have a coding efficiency of . This result means that every binary digit of the codeword provides at least 1-bit of information. We are maximally efficient with this encoding. If you think about it, if we send 1 symbol/s to the channel and our encoding has 1 symbol (e.g., TTT) is 3 bits long then essentially we are able to send 3 bits/s to the channel. Since bits/s, then we are utilizing the entire maximum channel capacity.
Channel Rate Example 2: A 6-sided Die
This time, suppose we want to send the symbols of a fair 6-sided die on a channel that only has bits/s (this is a separate given). Such that has outcomes . Of course, all outcomes are equiprobable with . From here, we can determined bits/symbol. Therefore:
symbols/s
Again, Shannon says that with a given and we can only transmit at a maximum symbol rate of symbols/s. Now, let's think of an encoding scheme that suits our needs. For convenience, to represent 6 unique outcomes, we can use 3 bits to represent each outcome. Let's say we have codebook-3:
Codebook-3
| Source Symbol | Codeword |
|---|---|
| 1 | 000 |
| 2 | 001 |
| 3 | 010 |
| 4 | 011 |
| 5 | 100 |
| 6 | 101 |
The coding efficiency of codebook-3 used for the 6-die example is:
Codebook-3 is not that efficient but it will suffice for now. Here, let's introduce the effective symbol rate due to the new encoding:
-
(4)
-
Our encoding scheme affects how much data we're putting into the channel. If our coding efficiency isn't optimal then we are only utilizing a fraction of the maximum capacity . Hence we have the effective channel transmission rate incorporated into our effective symbol rate . Calculating for codebook-3 would give:
symbols/s.
Observe that . We are not even close to the maximum rate. Can we find a better encoding? How about this, suppose we create a composite symbol that consists of the three 6-sided die symbols. For example, we can let be one symbol, or we can let be another symbol. If we do so, then we have around unique possible outcomes for the new set of symbols. To represent 216 outcomes we need a minimum of 8 bits of code length (because ). So we can have codebook-4 as:
Codebook-4
| Source Symbol | Codeword |
|---|---|
| 111 | 0000_0000 |
| 112 | 0000_0001 |
| 113 | 0000_0010 |
| ... | ... |
| 665 | 1101_0110 |
| 666 | 1101_0111 |
The underscores are just there to separate the 4 bits for clarity. Codebook-4 looks really long but in practice, it's still small. So what changes? Since we have 8 bits per 3 symbols, the effective code length per symbol is . Take note that all outcomes are equiprobable so dividing the 8 bits by 3 symbols is enough. This results in a coding efficiency of:
Cool! We're much closer to being maximally efficient. Now, let's compute the new for codebook-4:
symbols/s.
Superb! The new is close to the maximum rate of . The key trick was to create a composite symbols that consists of 3 of the original source symbols, then represent them with 8 binary digits of codewords.
Maximum Channel Capacity
This time, let's study how we can quantitatively determine the maximum channel capacity. In the last module, we comprehensively investigated the measures of , , and on a BSC. Recall that:
If you think about it, is a measure of channel quality. It tells us how much we can estimate the input from an observed output. is a measure of the received information contained in the source information. Ideally, if there is no noise, then resulting in . We want this because all the information from the source gets to the receiver! When noise is present , it degrades the quality of our and the information about the receiver contained in the source is now being shared with noise. This only means one thing: we want to be at maximum. From the previous discussion, we presented how varies with while parametrizing the noise probability . Figure 2 shows this plot. We can visualize like a pipe while the noise parameter limits the flow of information. Figure 3 GIF shows the pipe visualization.
In communication theory, is a metric for transmission rate. So the units are in bits/second. Interchanging between bits or bits/second might be confusing but for now, when we talk about channels (and also ), let's use bits/s. We can define the maximum channel capacity as:
-
(5)
-
We can re-write this as:
-
(5)
-
Here, is in units of bits/s. It tells us the maximum number of data that we can transmit per unit of time. Both and are affected by the noise parameter . In a way, noise limits . For example, a certain can only provide a certain maximum . Looking at figure 2, when (or ) we can get a maximum bits/s provided that the probability distribution of the symbols that get into the channel is . When (or ) we can also get a maximum bits/s when . Let's determine of a BSC given some and . Since we know follows the Bernoulli entropy where . Then we can write:
bits when . Since is fixed depending on a channel, we can manipulate the input probability of the source symbols that get into the channel such that we can force and achieve the maximum .
Interestingly, to achieve we simply need to set for any . The exception is when because that results in an absolute and will be undefined (i.e., ). This result shows that for any we can achieve maximum entropy for that given channel as long as we encode our source symbols to have before it gets into the channel! We can continue our derivation by writing as:
Leading to:
-
(6)
-
In equation 6, we can assume because we know we can achieve maximum entropy when we set . Equation 6 shows how the maximum capacity is limited by the noise . It describes the pipe visualization in figure 3. When , and our BSC has bits/s. When , , the noise entropy is at maximum and our channel has bits/s. Clearly, we can't transmit data this way. Lastly, when , then again and we're back to having bits/s.
The most important concept in determining maximum channel capacity is to use equation 5 for any channel model. Moreover, from our simple BSC derivation, we can see that in order to maximize the effective channel capacity, we need to encode our source symbols into codewords such that before it gets sent over the channel. This is the essence of the concept source coding where we encode the source to achieve maximum entropy. This is related to equation 4 where tells us the effective channel rate assuming we have not encoded our source symbols to achieve . If we have successfully achieved for the encoded codewords, then on average we utilize the maximum capacity (i.e., ).
Huffman Coding
The first two examples of encoding looked into source symbols that are equiprobable. First, we've shown that if , we can fully utilize the channel capacity. We've seen this in our three flips of a fair coin example. When , we had to duplicate the source symbols to so that the effective code efficiency and we can get closer to fully utilizing the channel. We're seeing a pattern that the closer our coding efficiency is to 1, we get closer to maximizing the channel capacity. However, what happens when the source symbols are not equiprobable?
Let's say we want to communicate the sum of two fair 6-sided die rolls. Our source alphabet contains symbols . The source probability distribution is shown in the table below:
| Source Symbol | Frequency | Probability |
|---|---|---|
| 2 | 1 | |
| 3 | 2 | |
| 4 | 3 | |
| 5 | 4 | |
| 6 | 5 | |
| 7 | 6 | |
| 8 | 5 | |
| 9 | 4 | |
| 10 | 3 | |
| 11 | 2 | |
| 12 | 1 |
What would be the best encoding for this source? The source entropy bits. Let's say codebook-5 is a simple binary representation. Since there are outcomes, then using 4 bits for each codeword will suffice. Codebook-5 is shown below:
Codebook-5
| Source Symbol | Codeword |
|---|---|
| 2 | 0000 |
| 3 | 0001 |
| 4 | 0010 |
| 5 | 0011 |
| 6 | 0100 |
| 7 | 0101 |
| 8 | 0110 |
| 9 | 0111 |
| 10 | 1000 |
| 11 | 1001 |
| 12 | 1010 |
Codebook-5 has and therefore the coding efficiency . Clearly this won't maximize the channel. Oh no! What should we do then? This is where we introduce one of the well-known compression methods: The Huffman Coding.
The Huffman coding is a lossless compression. The encoding has this interesting property where frequent symbols map to short codewords, while rare symbols map to long codewords. In fact, Huffman codes says that we can have an average code length of that's within a unit of then that means we'll have .
Huffman Coding Example 1
Let's consider another example before we show you the magic of the Huffman coding on our two-die roll scenario. Suppose we have a source alphabet with outcomes and probability distribution:
| Source Symbol | Probability |
|---|---|
| a | 0.05 |
| b | 0.25 |
| c | 0.37 |
| d | 0.22 |
| e | 0.11 |
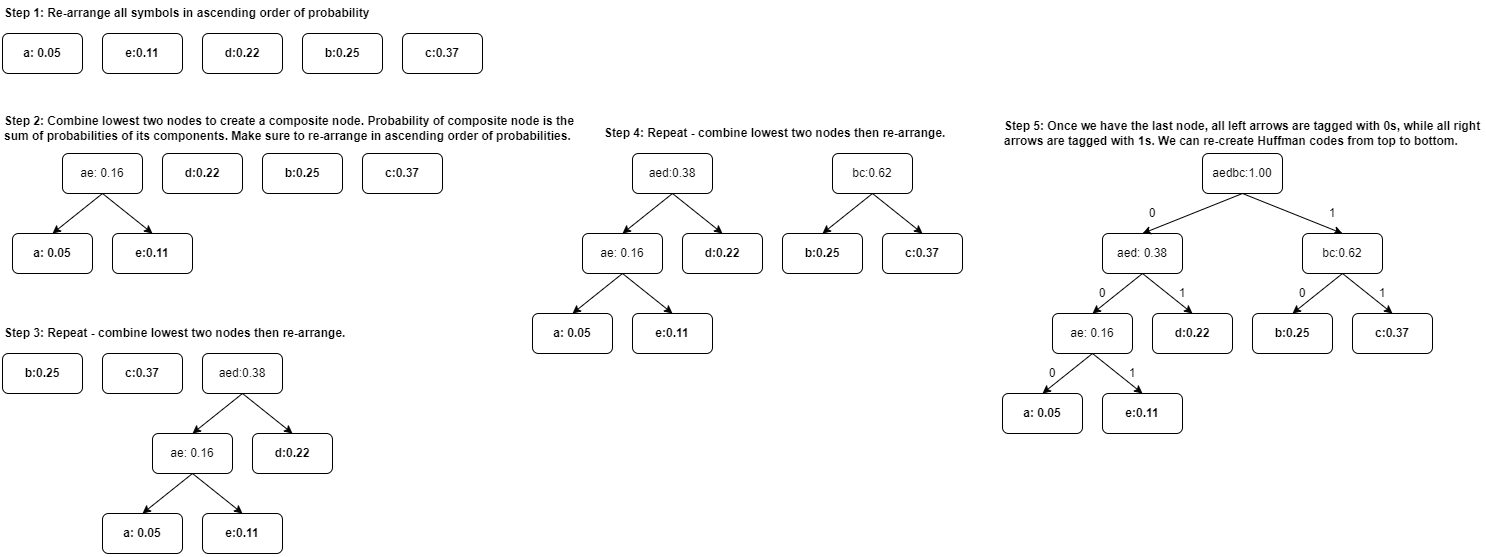
Huffman coding has the following steps:
1. Arrange all symbols in ascending order of their probability (or frequency). Let each symbol be a single leaf node.
2. Consider the bottom two nodes.
- Combine these two nodes to form a composite node.
- The probability of the composite node is the sum of its components.
- Make sure that the lower probability component is on the left of the composite node, while the higher probability component is on the right.
- If the components have the same probability, you can select either to be on the left or right.
3. Repeat step 1 and 2 with the new composite node as part of the list. Do this until we are left with 1 node.
- When you reach step 2 and a composite node has the same probability with another node (probably a composite node too), the node with the longer path takes the left side.
4. Write the Huffman codes starting from the top of the tree down to the root of the symbol.
- The top is the MSB (most-significant bit)
- The root of the tree are the LSB (least-significant bit)
Figure 4 shows a step-by-step process of reconstructing the tree of our example.
Just to explicitly explain the Huffman coding process:
1. We re-arranged elements to in ascending order of probabilities.
2. We combined the lowest two ( and ) to form the composite node whose probability is . We don't need to re-arrange because the elements are still in ascending order even with the composite node .
3. We combined with to get composite node with . We need to re-arrange the nodes in ascending order.
4. We combined and to get composite node with . We need to re-arrange the nodes in ascending order.
5. We reached the last tree so we just combined the composite nodes and . We should get if we did the Huffman code correctly. All left arrows are tagged with 0s while all right arrows are tagged with 1s. We can get the Huffman codes for all symbols from this tree. You can actually swap the directions for 1s and 0s, but for our example, all left arrows use 0s while all right arrows use 1s.
The top of the tree will be the MSB (left-most bit) while the bottom of the tree will be the LSB (right-most bit). For example, to get the Huffman code for we have (from the top of the tree) . To get we have . Simple right? We can generate a new codebook for our example.
Codebook for Huffman coding example 1
| Source Symbol | Codeword |
|---|---|
| a | 000 |
| b | 10 |
| c | 11 |
| d | 01 |
| e | 001 |
The cool part about Huffman coding is that codewords are uniquely decodable. This means that for every codeword, we can immediately tell the symbol it's pertaining to. We'll get back to this in the next module. For example, if the we received an encoded message we can decode it as . We can calculate the average code length for this one. Recall that:
Therefore, we have:
If we send these encoded symbols across a channel according to the probability distribution of each symbol, we would have on average. The entropy is:
bits
Therefore the coding efficiency for this example would be which is really close to being maximally efficient. Cool right? If we just represent each outcome with 3 binary digits (because there are 5 outcomes so we need ), then and the coding efficiency for a straight-forward binary coding would be . Huffman coding rules!
Huffman Coding Example 2
Just to make sure you have sufficient practice, let's try a different probability distribution for the same symbols:
| Source Symbol | Probability |
|---|---|
| a | 0.1 |
| b | 0.3 |
| c | 0.4 |
| d | 0.1 |
| e | 0.1 |
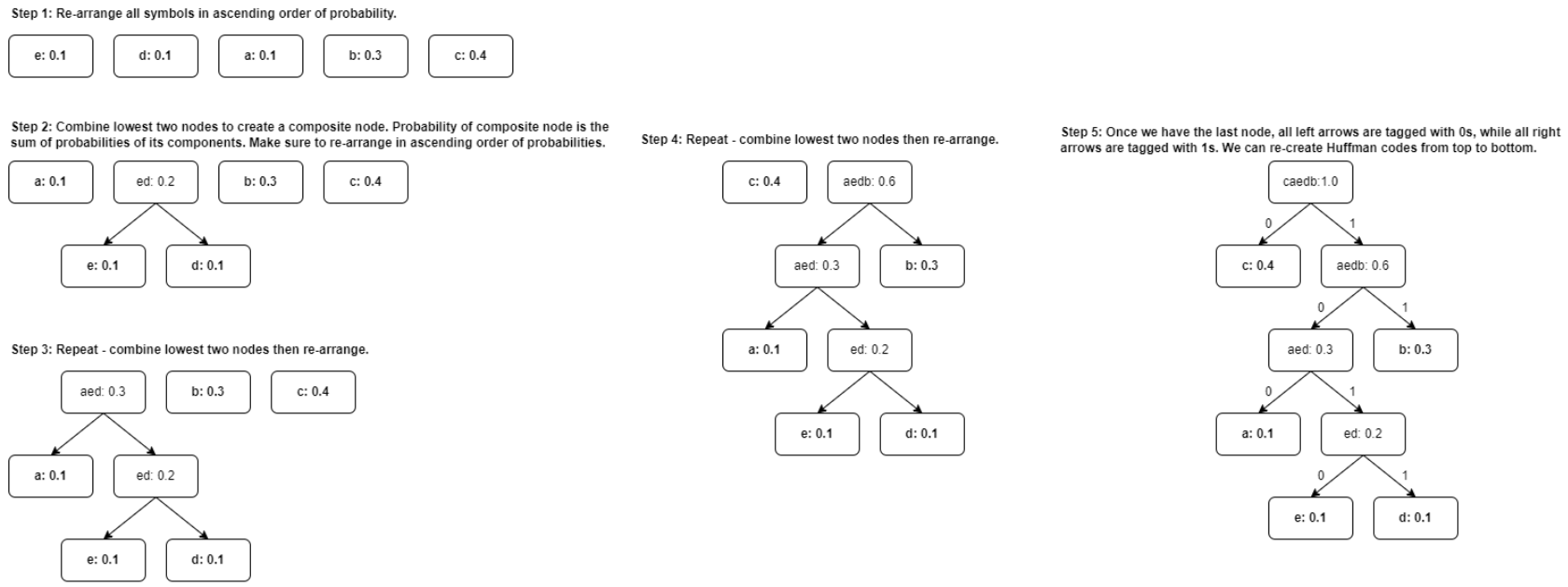
Figure 5 shows the Huffman coding process and steps.
1. We still re-arrange the symbols according to probability. In case the probabilities are the same, we can re-arrange them in any other way. However, sometimes it's more convenient to re-arrange them in alphabetical order of the symbol names. Or sometimes the symbol indices. It's entirely up to you.
2. Combine the lowest two: and to get with . Then re-arrange.
3. Combine the lowest two: and to get with . If a composite node has the same probability with other composite or base nodes, make sure the composite node with the highest depth stays on the left.
4. Combine with to get with . Re-arrange for the last node.
5. Last node should add up to 1. From here we tag all left arrows with 0s and all right arrows with 1s. We can construct our new codebook.
Codebook for Huffman coding example 2
| Source Symbol | Codeword |
|---|---|
| a | 100 |
| b | 11 |
| c | 0 |
| d | 1011 |
| e | 1010 |
The codebook for this example gives us an average codelength of:
While the source entropy would be:
Resulting in a coding efficiency of:
Still a much better coding efficiency that using a direct 3-bit binary representation because .
Huffman Coding Example 3
Going back to our 2-die roll example, we can use Huffman coding to get codebook 6:
Codebook-6
| Source Symbol | Codeword |
|---|---|
| 2 | 00101 |
| 3 | 1000 |
| 4 | 000 |
| 5 | 011 |
| 6 | 110 |
| 7 | 111 |
| 8 | 101 |
| 9 | 010 |
| 10 | 1001 |
| 11 | 0011 |
| 12 | 00100 |
Codebook-6 is just one table. Sometimes we may swap the direction of arrows. Moreover, sometimes when we end up having components of the same probabilities, we may have swapped them in a different direction. Regardless, the Huffman codes generate a mapping that is uniquely decodable. Codebook-6 has an average code length of . The two 6-sided die rolls has a source entropy of bits/s. Therefore . That is superbly close to a maximal coding efficiency. Lastly, if you observe all the Huffman encoding examples, all frequent symbols have shorter code lengths while all rare symbols have longer codelengths. This is a cool data compression algorithm.
Summary
For this chapter, we summarize our learnings:
- We covered the complete model for a channel while introducing components like encoder and decoder.
- We introduced new definitions: code symbols, codewords, codebooks, coding efficiency, maximum channel capacity, and effective channel rates.
- We had a sneak peak of the source coding theorem.
- We derived a quantitative measure of channel capacity for BSC.
- Lastly, we studied the Huffman coding and appreciated how cool it is.
Have fun doing the lab exercises 😃