Difference between revisions of "Information and entropy"
Ryan Antonio (talk | contribs) |
Ryan Antonio (talk | contribs) |
||
| (21 intermediate revisions by the same user not shown) | |||
| Line 5: | Line 5: | ||
From the last module's [[Engaging_introduction_to_information_theory|introduction]], information occurs in everyday life, and it consists of two aspects: ''surprise'' and ''meaning''. We would like to emphasize that our focus will be on the mathematics of surprise or uncertainty. Whenever you study a subject, you also experience a subtle application of information theory. For example, you are asked to review your elementary algebra again. You have confidence that the topic is easy, and you only need very little "brainpower" for the subject. It looks and feels easy because you are familiar with the material. You already have the information for the topic. Suppose you were asked to review your calculus subjects (e.g., Math 20 series) you may find it more challenging because most theories may or may not be familiar to you. There is a higher degree of ''uncertainty''. This time you need to exert more effort in studying. If you were asked to take on a new theory that you have no clue about, you have maximum uncertainty about that theory. However, once you have given enough time and effort to study that theory, that uncertainty now becomes acquired information for you. You may not need too much brainpower to review or teach that topic again. This leads to an important concept that may repeat in future discussions. We experience an uncertainty about a topic that we don't know about. However, when we "receive" that uncertainty, it becomes information. | From the last module's [[Engaging_introduction_to_information_theory|introduction]], information occurs in everyday life, and it consists of two aspects: ''surprise'' and ''meaning''. We would like to emphasize that our focus will be on the mathematics of surprise or uncertainty. Whenever you study a subject, you also experience a subtle application of information theory. For example, you are asked to review your elementary algebra again. You have confidence that the topic is easy, and you only need very little "brainpower" for the subject. It looks and feels easy because you are familiar with the material. You already have the information for the topic. Suppose you were asked to review your calculus subjects (e.g., Math 20 series) you may find it more challenging because most theories may or may not be familiar to you. There is a higher degree of ''uncertainty''. This time you need to exert more effort in studying. If you were asked to take on a new theory that you have no clue about, you have maximum uncertainty about that theory. However, once you have given enough time and effort to study that theory, that uncertainty now becomes acquired information for you. You may not need too much brainpower to review or teach that topic again. This leads to an important concept that may repeat in future discussions. We experience an uncertainty about a topic that we don't know about. However, when we "receive" that uncertainty, it becomes information. | ||
| − | There is a subtle tradeoff between uncertainty and brainpower for a particular subject. You will start to notice this later in the course. Observe that when there is high uncertainty (e.g., a completely new topic), our brain exerts effort to study a material. Whenever we have low uncertainty (e.g., review a familiar subject), we exert less effort for the subject. The amount of brainpower that we use can be analogous to computing power. | + | There is a subtle tradeoff between uncertainty and brainpower for a particular subject. You will start to notice this later in the course. Observe that when there is high uncertainty (e.g., a completely new topic), our brain exerts effort to study a material. Whenever we have low uncertainty (e.g., review a familiar subject), we exert less effort for the subject. The amount of brainpower that we use can be analogous to computing power. We associate uncertainty to the data that we need to process. This example shows where information theory and complexity mix together. If we are given a similar problem, what would be the best solution? Information theory does not tell us how to solve a problem because it is only a measurement. The solutions are up to us. Going back to our study example, if we need to study a completely new topic, what are our options? Do we spend so much time on the material to cover the bulk of it? How much brainpower do we use? Or can we cut the material into chunks so that we can process it with optimum speed and power? The solution is up to us. We just need to be creative. |
| − | {{Note| Chunking is a well-known learning strategy to reduce the workload on a particular subject. It is proven to be effective in studying new topics. You can find several Youtube videos on chunking. Go ahead and try. <ref> Sousa, David A. 2006. How the | + | {{Note| Chunking is a well-known learning strategy to reduce the workload on a particular subject. It is proven to be effective in studying new topics. You can find several Youtube videos on chunking. Go ahead and try. <ref> Sousa, David A. 2006. ''How the Brain Learns''. Thousand Oaks, Calif: Corwin Press. </ref> |reminder}} |
== Deriving Information == | == Deriving Information == | ||
| Line 14: | Line 14: | ||
# <math> I(e) </math> should be a decreasing function of <math> P(e) </math>. The same goes for event <math> f </math>. | # <math> I(e) </math> should be a decreasing function of <math> P(e) </math>. The same goes for event <math> f </math>. | ||
| − | # If the two events have <math> P(e) \leq P(f) </math> then it should follow that <math> I(e) \geq I(f) </math>. | + | # If the two events have <math> P(e) \leq P(f) </math> then it should follow that <math> I(e) \geq I(f) </math>. A more surprising event should have higher information. |
# Since both events are independent, then <math> I(e \cap f) = I(e) + I(f) </math>. Also, following from the previous item: <math> I(e \cap f) \geq I(e) \geq I(f) </math>. | # Since both events are independent, then <math> I(e \cap f) = I(e) + I(f) </math>. Also, following from the previous item: <math> I(e \cap f) \geq I(e) \geq I(f) </math>. | ||
| − | Let's look at a simple example. Suppose we'll be drawing a card from a pack of 52 casino cards. | + | Let's look at a simple example. Suppose we'll be drawing a card from a pack of 52 casino cards. What is the probability when the drawn card is: |
* A club. Let this be event <math> a </math>. | * A club. Let this be event <math> a </math>. | ||
| Line 29: | Line 29: | ||
* <math> P(a \cap b) = \frac{1}{52} </math> | * <math> P(a \cap b) = \frac{1}{52} </math> | ||
| − | Since we know the probabilities and the desired properties for Shannon's theorem, we | + | Since we know the probabilities and the desired properties for Shannon's theorem, we should observe the following: <math> I(b) \geq I(a) </math> because it is more surprising to draw an ace compared to drawing any card that is a club. <math> I(a \cap b) \geq I(b) \geq I(a) </math> because it is a lot more surprising to get the ace of clubs compared to the individual events. Moreover, our intuition tells us that <math> I( a \cap b) = I(b) + I(a) </math>. The question is, what kind of function should information be if we know the probabilities of each event? After hours of thinking, Shannon came up with: |
| Line 43: | Line 43: | ||
So either way works and we'll call them equation 1. Let's apply these in action, if we calculate the information for events <math> a </math>, <math> b </math>, and <math> a \cap b </math>. | So either way works and we'll call them equation 1. Let's apply these in action, if we calculate the information for events <math> a </math>, <math> b </math>, and <math> a \cap b </math>. | ||
| − | * <math> I(a) = - | + | * <math> I(a) = -\log_2 \left( \frac{1}{4} \right) = 2 \ \textrm{bits} </math> |
| − | * <math> I(b) = - | + | * <math> I(b) = -\log_2 \left( \frac{1}{13} \right) = 3.70 \ \textrm{bits} </math> |
| − | * <math> I(a \cap b) = - | + | * <math> I(a \cap b) = -\log_2 \left( \frac{1}{52} \right) = 5.70 \ \textrm{bits} </math> |
It satisfies everything we agreed upon! | It satisfies everything we agreed upon! | ||
| Line 75: | Line 75: | ||
! scope="col"| <math> I(0.25) </math> | ! scope="col"| <math> I(0.25) </math> | ||
|- | |- | ||
| − | | 2 | + | | style="text-align:center;" | 2 |
| − | | bits (from ''binary'') | + | | style="text-align:center;" | bits (from ''binary'') |
| − | | 2.00 | + | | style="text-align:center;" | 2.00 |
|- | |- | ||
| − | | 3 | + | | style="text-align:center;" | 3 |
| − | | trits (from ''trinary'') | + | | style="text-align:center;" | trits (from ''trinary'') |
| − | | 1.26 | + | | style="text-align:center;" | 1.26 |
|- | |- | ||
| − | | <math>e</math> | + | | style="text-align:center;" | <math>e</math> |
| − | | nats (from ''natural logarithm'') | + | | style="text-align:center;" | nats (from ''natural logarithm'') |
| − | | 1.38 | + | | style="text-align:center;" | 1.38 |
|- | |- | ||
| − | | 10 | + | | style="text-align:center;" | 10 |
| − | | bans | + | | style="text-align:center;" | bans |
| − | | 0.602 | + | | style="text-align:center;" | 0.602 |
|- | |- | ||
|} | |} | ||
| Line 104: | Line 104: | ||
|- | |- | ||
|Someone tells you <math>1=1</math>. | |Someone tells you <math>1=1</math>. | ||
| − | |<math>1</math> | + | |style="text-align:center;" | <math>1</math> |
| − | |<math>\log_2\left(1\right) = 0</math> | + | |style="text-align:center;" | <math>\log_2\left(1\right) = 0</math> |
|- | |- | ||
| You got the wrong answer on a 4-choice multiple choice question. | | You got the wrong answer on a 4-choice multiple choice question. | ||
| − | |<math>\frac{3}{4}</math> | + | |style="text-align:center;" | <math>\frac{3}{4}</math> |
| − | |<math>\log_2\left(\frac{4}{3}\right)=0.415\,\mathrm{bits}</math> | + | |style="text-align:center;" | <math>\log_2\left(\frac{4}{3}\right)=0.415\,\mathrm{bits}</math> |
|- | |- | ||
| You guessed correctly on a 4-choice multiple choice question. | | You guessed correctly on a 4-choice multiple choice question. | ||
| − | |<math>\frac{1}{4}</math> | + | |style="text-align:center;" | <math>\frac{1}{4}</math> |
| − | |<math>\log_2\left(4\right)=2\,\mathrm{bits}</math> | + | |style="text-align:center;" | <math>\log_2\left(4\right)=2\,\mathrm{bits}</math> |
|- | |- | ||
| You got the correct answer in a True or False question. | | You got the correct answer in a True or False question. | ||
| − | |<math>\frac{1}{2}</math> | + | |style="text-align:center;" | <math>\frac{1}{2}</math> |
| − | |<math>\log_2\left(2\right)=1\,\mathrm{bit}</math> | + | |style="text-align:center;" | <math>\log_2\left(2\right)=1\,\mathrm{bit}</math> |
|- | |- | ||
| You rolled a seven on rolling a pair of dice. | | You rolled a seven on rolling a pair of dice. | ||
| − | |<math>\frac{6}{36}</math> | + | |style="text-align:center;" | <math>\frac{6}{36}</math> |
| − | |<math>\log_2\left(6\right)=2.58\,\mathrm{bits}</math> | + | |style="text-align:center;" | <math>\log_2\left(6\right)=2.58\,\mathrm{bits}</math> |
|- | |- | ||
| Winning the Ultra Lotto 6/58 jackpot. | | Winning the Ultra Lotto 6/58 jackpot. | ||
| − | |<math>\frac{1}{40400000}</math> | + | |style="text-align:center;" | <math>\frac{1}{40400000}</math> |
| − | |<math>\log_2\left(40400000\right)=25.27\,\mathrm{bits}</math> | + | |style="text-align:center;" | <math>\log_2\left(40400000\right)=25.27\,\mathrm{bits}</math> |
|- | |- | ||
|} | |} | ||
| Line 132: | Line 132: | ||
== Entropy == | == Entropy == | ||
| + | |||
| + | Information is a measure of surprise for one event only. We can expand this to a collection of events encapsulated with some random variable <math> X </math>. Recall that a random variable contains a set of outcomes <math> \{x_1,x_2,x_3,...,x_n \} </math> and each outcome has an associated probability <math> \{P(x_1), P(x_2), P(x_3), ... ,P(x_n) \} </math>. Each outcome also has its own set of information <math> \{I(x_1), I(x_2), I(x_3), ... ,I(x_n) \} </math>. We can get the mean of all <math> I(X) </math>. We call this ''entropy'' which we denote with <math> H(X) </math>: | ||
| + | |||
| + | |||
| + | {{NumBlk|::|<math> H(X) = E(I(X)) = - \sum_{i=1}^n P(x_i) \log_2 \left(P(x_i)\right) </math>|{{EquationRef|2}}}} | ||
| + | |||
| + | |||
| + | Entropy is just the mean of information for some random variable <math> X </math>. Let's look at a few examples. Consider some random variable <math> X </math> with outcomes <math> \{x_1, x_2, x_3, x_4, x_5, x_6, x_7, x_8 \} </math>. All outcomes have a probability of <math> \{P(x_1) = P(x_2) = P(x_3) = P(x_4) = P(x_5) = P(x_6) = P(x_7) = P(x_8) = \frac{1}{8} \} </math>. What is <math> H(X) </math>? Simple! | ||
| + | |||
| + | <math> | ||
| + | \begin{align} | ||
| + | H(X) &= - \sum_{i=1}^n P(x_i) \log_2 \left(P(x_i)\right) \\ | ||
| + | &= -8 \cdot \frac{1}{8} \log_2 \left( \frac{1}{8} \right) \\ | ||
| + | &= 3.00 \ \textrm{bits} | ||
| + | \end{align} </math> | ||
| + | |||
| + | Therefore, the average information for the simple uniform distribution is <math> 3.00 </math> bits. Let's take a look at another example. Suppose we flip a fair coin three times. Let the random variable <math> X </math> be the sum of heads in those three flips. What is <math> H(X) </math>? It's easier to tabulate the data. | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! scope="col"| <math> x_i </math> | ||
| + | ! scope="col"| <math> P(X = x_i) </math> | ||
| + | ! scope="col"| <math> I(X = x_i) </math> | ||
| + | ! scope="col"| <math> P(X = x_i)I(X = x_i) </math> | ||
| + | |- | ||
| + | | style="text-align:center;" | <math> 0 </math> | ||
| + | | style="text-align:center;" | <math> \frac{1}{8} </math> | ||
| + | | style="text-align:center;" | <math> 3.00 </math> | ||
| + | | style="text-align:center;" | <math> 0.375 </math> | ||
| + | |- | ||
| + | | style="text-align:center;" | <math> 1 </math> | ||
| + | | style="text-align:center;" | <math> \frac{3}{8} </math> | ||
| + | | style="text-align:center;" | <math> 1.415 </math> | ||
| + | | style="text-align:center;" | <math> 0.531 </math> | ||
| + | |- | ||
| + | | style="text-align:center;" | <math> 2 </math> | ||
| + | | style="text-align:center;" | <math> \frac{3}{8} </math> | ||
| + | | style="text-align:center;" | <math> 1.415 </math> | ||
| + | | style="text-align:center;" | <math> 0.531 </math> | ||
| + | |- | ||
| + | | style="text-align:center;" | <math> 3 </math> | ||
| + | | style="text-align:center;" | <math> \frac{1}{8} </math> | ||
| + | | style="text-align:center;" | <math> 3.00 </math> | ||
| + | | style="text-align:center;" | <math> 0.375 </math> | ||
| + | |- | ||
| + | |} | ||
| + | |||
| + | Summing all <math> P(X = x_i)I(X = x_i) </math> terms we get: | ||
| + | |||
| + | <math> H(X) = P(X = 0)I(X = 0) + P(X = 1)I(X = 1) + P(X = 2)I(X = 2) + P(X = 3)I(X = 3) = 1.81 \ \textrm{bits} </math> | ||
=== Bounds of Entropy === | === Bounds of Entropy === | ||
| + | |||
| + | Entropy has bounds, meaning there is a lower and upper limit to this value. Just like in any system, these bounds serve as limitations to our measurement. In a nutshell, for any random variable <math> X </math> with <math> n </math> outcomes, the bounds of entropy is: | ||
| + | |||
| + | |||
| + | {{NumBlk|::|<math> 0 \leq H(X) \leq \log(n) </math>|{{EquationRef|3}}}} | ||
| + | |||
| + | |||
| + | The lower bound <math> H(X) \geq 0 </math> occurs if and only if one of the outcomes has absolute certainty (i.e., <math> P(X = x_i) = 1 </math>). This is trivial. Recall that for a random variable <math> X </math> with outcomes <math> \{x_1, x_2, ..., x_n \} </math> and their associated probabilities <math> \{P(x_1), P(x_2), ..., P(x_n) \} </math>. The sum of all probabilities must sum up to 1. Such that: | ||
| + | |||
| + | <math> \sum_{i=1}^n P(X = x_i) = 1 </math> | ||
| + | |||
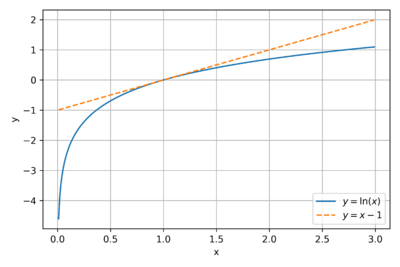
| + | [[File:Gibbs Inequality.png|thumb|400px|Figure 1: The plot of <math>y = \ln\left(x\right)</math> and <math>y = x - 1</math>.]] | ||
| + | |||
| + | If one of the elements has absolute certainty: <math> P(X = x_i) = 1 </math> then that means all other probabilities need to be <math> P(X = x_j) = 0 </math> where <math> i \neq j</math>. Solving for <math> H(X) = 0 </math> if this happens. | ||
| + | |||
| + | |||
| + | |||
| + | The upper bound is a bit tricky. First we need to recognize a fact that <math> \ln (x) \leq x - 1</math> with equality if and only if <math> x = 1 </math>. When we say "with equality" then that means the equal sign holds true if and only if the condition is met. This is trivial: <math> \ln (x) \leq x-1 \rightarrow \ln(1) = 1 - 1 \rightarrow 0 = 0</math> if and only if <math> x = 1 </math>. We can also observe <math> \ln (x) </math> and <math> x - 1 </math> from figure 1. | ||
| + | |||
| + | Second, we need to appreciate what Gibbs inequality tells us. Suppose we have two probability distributions <math> P = \{p_1,p_2,...,p_n\} </math> and <math> Q = \{q_1, q_2, ..., q_n\} </math>. Also note that <math> \sum_{i=1}^n p_i = 1</math> and <math> \sum_{i=1}^n q_i = 1</math>. Gibbs inequality says: | ||
| + | |||
| + | {{NumBlk|::|<math> \sum_{i=1}^n p_i \ln \left(\frac{q_i}{p_i} \right) \leq \sum_{i=1}^n p_i \left(\frac{q_i}{p_i} - 1 \right) </math> |{{EquationRef|4}}}} | ||
| + | |||
| + | Simplifying the right handside results in: | ||
| + | |||
| + | <math> \sum_{i=1}^n \left(q_i - p_i \right) = \sum_{i=1}^n q_i - \sum_{i=1}^n p_i = 1 - 1 = 0 </math> | ||
| + | |||
| + | In other words, Gibbs inequality says that: | ||
| + | |||
| + | {{NumBlk|::|<math> \sum_{i=1}^n p_i \ln \left(\frac{q_i}{p_i} \right) = 0 </math> |{{EquationRef|5}}}} | ||
| + | |||
| + | If and only if <math>p_i = q_i </math> for all <math> i </math>. Take note of equation 5 and its condition for being true. We will use this result for deriving the upper bound. Now, let's consider a random variable <math> X </math> with probability distribution <math> P = \{p_1, p_2, ... ,p_n \} </math>. Let's find what kind of distribution maximizes the entropy function. We have: | ||
| + | |||
| + | <math> | ||
| + | \begin{align} | ||
| + | H(P) - \log (n) &= \sum_{i=1}^n p_i \log \left( \frac{1}{p_i}\right) - \log (n) \\ | ||
| + | &= \sum_{i=1}^n p_i \log \left( \frac{1}{p_i}\right) - \sum_{i=1}^n p_i \log (n) \\ | ||
| + | &= \sum_{i=1}^n p_i \left( \log \left( \frac{1}{p_i}\right) - \log (n) \right) \\ | ||
| + | &= \sum_{i=1}^n p_i \log \left( \frac{\frac{1}{n}}{p_i} \right) \\ | ||
| + | &\leq 0 | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |||
| + | The second step works because we know that <math> \sum_{i=1}^n p_i = 1 </math>. The last step works because of Gibbs inequality (i.e., <math> \sum_{i=1}^n p_i \ln \left(\frac{q_i}{p_i} \right) = 0 </math>). Therefore <math> H(P) - \log(n) = 0 </math> works if and only if <math> p_i = \frac{1}{n} </math> for all <math> i </math>. | ||
| + | |||
| + | '''In plain English, this means that we attain maximum entropy if and only if all outcomes are equiprobable!''' | ||
| + | |||
| + | In summary, the bounds of entropy can be summarized as <math> 0 \leq H(X) \leq \log(n) </math>. | ||
| + | * The lower bound occurs if at least one outcome has absolute certainty <math> p_i = 1 </math>. | ||
| + | * The upper bound occurs if all outcomes are equiprobable <math> p_i = \frac{1}{n} </math>. Assuming there are <math> n </math> outcomes. | ||
=== Interpreting Entropy === | === Interpreting Entropy === | ||
| + | There are several ways to interpret entropy. Here, we'll use binary trees as a graphical representation <ref> Stone, J.V. , ''Information Theory: A Tutorial Introduction'', Sebtel Press, 2015. </ref>. It's easier to appreciate a concept if we associate it to something. In the previous examples, we use bits as our units of information. Take note that our definition of bit is a definite amount of information. It is common to use bits because it suits the binary system which we will see in the succeeding discussions. | ||
| + | |||
| + | Suppose we're in a role-playing game where we have control of the ending of our hero. Let this be random variable <math> X </math> which contains outcomes <math> \{ a,b,c,d,e,f,g,h\} </math>. There are <math> n = 8 </math> alternate endings for our hero's story. The decision tree for our hero is shown in figure 3. For now, let's also assume that at every node, our hero can take the left or the right path with probabilities <math> P(\textrm{left}) = P(\textrm{right}) = 0.5 </math>. Let's say the game designer made it this way such that the player experiences these paths. Since all <math> P(a) = P(b) = P(c) = P(d) = P(e) = P(f) = P(g) = P(h) = 0.125 </math> then each ending is equiprobable and the entropy is <math> H(X) = 3.00 </math> bits of information. | ||
| + | |||
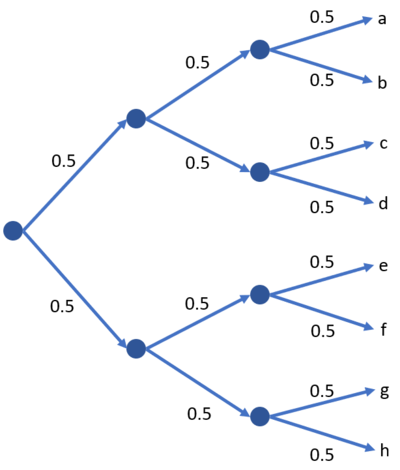
| + | [[File:Uniform tree.PNG|400px|thumb|center|Figure 3: Decision tree with equiprobable endings. This results in maximum entropy of <math> 3.00 </math> bits.]] | ||
| + | |||
| + | Here's why bits is such a convenient unit for information. If we know the entropy <math> H(X) </math> then it also means we have <math> m = 2^{H(X)}</math> ''equiprobable outcomes''. In our example, since we know that the entropy is <math> H(X) = 3 </math> then that also translates to <math> m = 2^{H(X)} = 2^3 = 8 </math> equiprobable outcomes. Keep this interpretation in mind. If we forget, we can always go back to this idea. | ||
| + | |||
| + | Now, suppose the game designer changed all the probabilities for each left and right path to spice up the game. Figure 4 shows a decision tree with varying probabilities per path. | ||
| + | |||
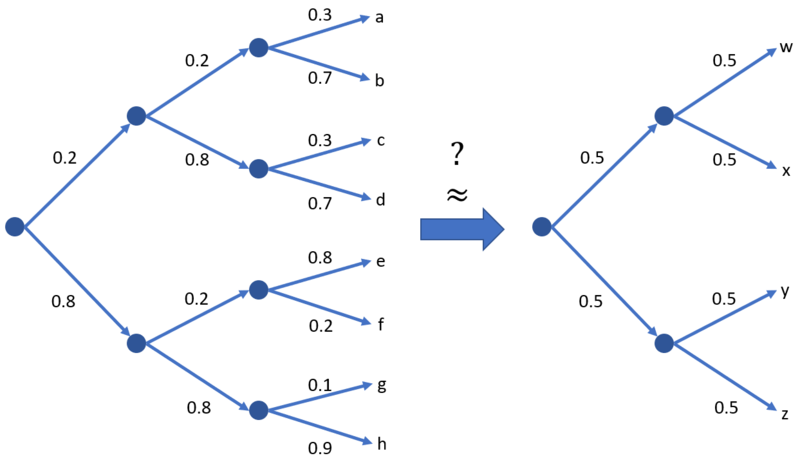
| + | [[File:Nonuniform tree.PNG|800px|thumb|center| Figure 4: Nonuniform distribution for the endings. Entropy for this is <math> H(X) \approx 2.04 </math> bits.]] | ||
| + | |||
| + | The probabilities of each ending are: | ||
| + | |||
| + | * <math> P(a) = 0.012 </math> | ||
| + | * <math> P(b) = 0.028 </math> | ||
| + | * <math> P(c) = 0.048 </math> | ||
| + | * <math> P(d) = 0.112 </math> | ||
| + | * <math> P(e) = 0.128 </math> | ||
| + | * <math> P(f) = 0.032 </math> | ||
| + | * <math> P(g) = 0.064 </math> | ||
| + | * <math> P(h) = 0.576 </math> | ||
| + | |||
| + | Calculating the entropy would give us <math> H(X) = 2.03578 </math> bits of information. Remember, we mentioned that given some <math> H(X) </math> we can think of it as having <math> m = 2^{H(X)} = 2^{2.03578} \approx 4.1 </math> equiprobable outcomes. Of course, drawing 4.1 different outcomes is impossible with binary trees but let's approximate it to 4. What does this mean? If the distribution of the outcomes follows that of what is in figure 4, then having 8 outcomes for the ending is almost as good as having 4 ''equiprobable'' endings! This implies that if a thousand players (or more) play the game with the non-uniform distribution of endings, then it's as good as playing a game with only 4 endings. The catch is that we don't know those outcomes. It could be a direct combination of existing outcomes (e.g., ending a and b are combined), or a mixture of partitioned outcomes (e.g., a piece of ending h, g, and d can be combined together). Of course, the uniform distribution tree will be more exciting if all 8 outcomes are equiprobable. It's consistent because its entropy <math> H(X) = 3 </math> bits indicates that it is more surprising. The non-uniform distribution tree will be less exciting because it's effectively equivalent to 4 outcomes only. Wherein it's also consistent with its entropy because <math> H(X) = 2 </math> bits is less surprising compared to the uniform distribution. | ||
| + | |||
| + | |||
| + | '''In summary, one good interpretation of entropy is that if we are given <math> H(X) </math> bits of information (or uncertainty) then we are "effectively" looking at a system that has <math> m = 2^{H(X)} </math> equiprobable outcomes.''' | ||
| + | |||
| + | |||
| + | {{Note| '''So do we actually want high entropy or low entropy?''' We want high entropy because it is equivalent to the amount of information that we can get once that event or outcome is given (or happens) to us. When we calculate uncertainty, the information about that event is the amount of information that we don't have. If that event happens, then we gain that uncertainty. Effectively, we gain that same amount of information. We'll revisit this when we discuss ''joint entropy'', ''conditional entropy'', and ''mutual information''. Stay tuned! |reminder}} | ||
| + | |||
| + | == A Dicey Example == | ||
| + | |||
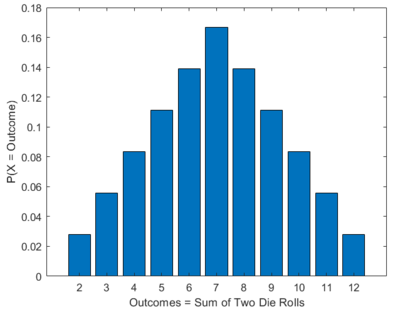
| + | [[File:Bar graph.PNG|thumb|400px|right|Figure 6: Bar graph for the probability distribution of the sum of two die rolls.]] | ||
| + | |||
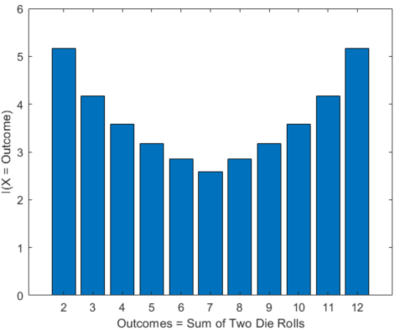
| + | [[File:Info_2die_roll.PNG|thumb|400px|right|Figure 7: Bar graph for the information distribution of the sum of two die rolls.]] | ||
| + | |||
| + | Suppose you were to roll two fair 6-sided dies. Let the random variable <math> X </math> be the sum of the two dies. Do the following: | ||
| + | |||
| + | (a) Tabulate the outcomes, the probability of each outcome, the information of each outcome. | ||
| + | |||
| + | (b) Calculate the entropy of <math> H(X) </math>. | ||
| + | |||
| + | (c) Interpret what it means to have <math> H(X) </math> bits of information for this experiment. | ||
| + | |||
| + | |||
| + | '''Solution''' | ||
| + | |||
| + | (a) The table below is the answer. We'll leave it up to you how the probabilities and information is computed. | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! scope="col"| Outcome <math> x_i </math> | ||
| + | ! scope="col"| <math> P(X = x_i) </math> | ||
| + | ! scope="col"| <math> I(X = x_i) </math> (bits) | ||
| + | |- | ||
| + | | style="text-align:center;" | <math> 2 </math> | ||
| + | | style="text-align:center;" | <math> \frac{1}{36} </math> | ||
| + | | style="text-align:center;" | <math> 5.17 </math> | ||
| + | |- | ||
| + | | style="text-align:center;" | <math> 3 </math> | ||
| + | | style="text-align:center;" | <math> \frac{1}{18} </math> | ||
| + | | style="text-align:center;" | <math> 4.17 </math> | ||
| + | |- | ||
| + | | style="text-align:center;" | <math> 4 </math> | ||
| + | | style="text-align:center;" | <math> \frac{1}{12} </math> | ||
| + | | style="text-align:center;" | <math> 3.58 </math> | ||
| + | |- | ||
| + | | style="text-align:center;" | <math> 5 </math> | ||
| + | | style="text-align:center;" | <math> \frac{1}{9} </math> | ||
| + | | style="text-align:center;" | <math> 3.17 </math> | ||
| + | |- | ||
| + | | style="text-align:center;" | <math> 6 </math> | ||
| + | | style="text-align:center;" | <math> \frac{5}{36} </math> | ||
| + | | style="text-align:center;" | <math> 2.85 </math> | ||
| + | |- | ||
| + | | style="text-align:center;" | <math> 7 </math> | ||
| + | | style="text-align:center;" | <math> \frac{1}{6} </math> | ||
| + | | style="text-align:center;" | <math> 2.58 </math> | ||
| + | |- | ||
| + | | style="text-align:center;" | <math> 8 </math> | ||
| + | | style="text-align:center;" | <math> \frac{5}{36} </math> | ||
| + | | style="text-align:center;" | <math> 2.85 </math> | ||
| + | |- | ||
| + | | style="text-align:center;" | <math> 9 </math> | ||
| + | | style="text-align:center;" | <math> \frac{1}{9} </math> | ||
| + | | style="text-align:center;" | <math> 3.17 </math> | ||
| + | |- | ||
| + | | style="text-align:center;" | <math> 10 </math> | ||
| + | | style="text-align:center;" | <math> \frac{1}{12} </math> | ||
| + | | style="text-align:center;" | <math> 3.58 </math> | ||
| + | |- | ||
| + | | style="text-align:center;" | <math> 11 </math> | ||
| + | | style="text-align:center;" | <math> \frac{1}{18} </math> | ||
| + | | style="text-align:center;" | <math> 4.17 </math> | ||
| + | |- | ||
| + | | style="text-align:center;" | <math> 12 </math> | ||
| + | | style="text-align:center;" | <math> \frac{1}{36} </math> | ||
| + | | style="text-align:center;" | <math> 5.17 </math> | ||
| + | |- | ||
| + | |} | ||
| + | |||
| + | (b) Use equation 2 to solve for the entropy. It's written below for convenience. | ||
| + | |||
| + | <math> H(X) = - \sum_{i=1}^n P(x_i) \log_2 (P(x_i)) </math> | ||
| + | |||
| + | |||
| + | <math> H(X) = -\frac{1}{36} \log_2 \left( \frac{1}{36} \right) -\frac{1}{18} \log_2 \left( \frac{1}{18} \right) -\frac{1}{12} \log_2 \left( \frac{1}{12} \right) -\frac{1}{9} \log_2 \left( \frac{1}{9} \right) -\frac{5}{36} \log_2 \left( \frac{5}{36} \right) -\frac{1}{6} \log_2 \left( \frac{1}{6} \right) -\frac{5}{36} \log_2 \left( \frac{5}{36} \right) -\frac{1}{9} \log_2 \left( \frac{1}{9} \right) -\frac{1}{12} \log_2 \left( \frac{1}{12} \right) -\frac{1}{18} \log_2 \left( \frac{1}{18} \right) -\frac{1}{36} \log_2 \left( \frac{1}{36} \right)</math> | ||
| + | |||
| + | |||
| + | <math> H(X) = 3.2744 </math> bits of information. | ||
| + | |||
| + | |||
| + | (c) From the previous discussion, it appears that this experiment is equivalent to <math> m = 2^{H(X)} \approx 9.68 </math> equiprobable outcomes. The 2 die rolls can be an equivalent binary tree system that produces 9.68 equiprobable outcomes. It can't really happen in reality but you get the idea. The entropy of the sum of two die rolls is more surprising than drawing any club in a deck of 52 casino cards (i.e., <math> I(\textrm{Clubs}) = 2 </math> bits of information). It's a little less surprising than drawing any ace of cards (i.e., <math> I(\textrm{Ace}) = 3.70 </math> bits of information). It's much less surprising than drawing an ace of clubs (i.e., <math> I(\textrm{AceClubs}) = 5.70 </math> bits of information). Again, we emphasize that entropy and information are measures of uncertainty. Cool right? | ||
| + | |||
| + | == Bernoulli Entropy == | ||
| + | |||
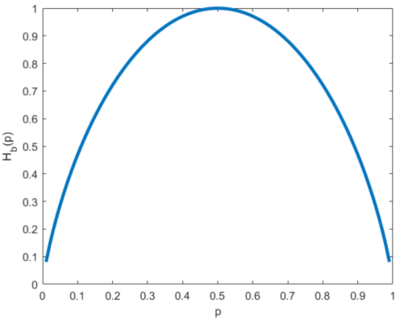
| + | [[File:Bernoulli entropy.PNG|400px|thumb|right|Figure 8: Bernoulli entropy <math> H_b(p) </math> with varying <math> p </math>]] | ||
| − | + | Often times, we prefer to write equations and use a computer to assist us in our analysis. Recall that a Bernoulli trial is an outcome with probability <math> p </math> for getting a success. The probability <math> 1 - p</math> is for failing. We usually use this for the coin toss problem. Let's define <math> H_b(p) </math> to be the entropy of a Bernoulli trial written as: | |
| − | = | + | {{NumBlk|::|<math> H_b(p) = -p \log_2 (p) - (1-p) \log_2 (1-p) </math>|{{EquationRef|6}}}} |
| − | + | Writing the equation this way is convenient and easy for the reader. The first term on the right hand side is the component for getting a success while the second term is the component for getting a fail. You just need to program this (e.g., Python, MATLAB, or C) and you can plot how the entropy varies with changing <math> p </math>. Figure 8 shows how the entropy changes with varying <math> p </math>. Let's look at a few numbers: | |
| − | === | + | * <math> p = 0.95 </math> yields <math> H_b(p) = 0.286 </math> bits. |
| + | * <math> p = 0.60 </math> yields <math> H_b(p) = 0.971 </math> bits. | ||
| + | * <math> p = 0.50 </math> yields <math> H_b(p) = 1.000 </math> bits. | ||
| + | * <math> p = 0.40 </math> yields <math> H_b(p) = 0.971 </math> bits. | ||
| + | * <math> p = 0.05 </math> yields <math> H_b(p) = 0.286 </math> bits. | ||
| + | Observe that the entropy is symmetric. The entropy when we are likely to succeed is the same as we are likely to fail (e.g., <math> p = 0.95 </math> and <math> p = 0.05 </math>). The highest entropy is when we are unsure of winning or failing (e.g., <math> p = 0.5 </math>). | ||
== References == | == References == | ||
Latest revision as of 08:04, 28 February 2022
Contents
Before We Begin ...
From the last module's introduction, information occurs in everyday life, and it consists of two aspects: surprise and meaning. We would like to emphasize that our focus will be on the mathematics of surprise or uncertainty. Whenever you study a subject, you also experience a subtle application of information theory. For example, you are asked to review your elementary algebra again. You have confidence that the topic is easy, and you only need very little "brainpower" for the subject. It looks and feels easy because you are familiar with the material. You already have the information for the topic. Suppose you were asked to review your calculus subjects (e.g., Math 20 series) you may find it more challenging because most theories may or may not be familiar to you. There is a higher degree of uncertainty. This time you need to exert more effort in studying. If you were asked to take on a new theory that you have no clue about, you have maximum uncertainty about that theory. However, once you have given enough time and effort to study that theory, that uncertainty now becomes acquired information for you. You may not need too much brainpower to review or teach that topic again. This leads to an important concept that may repeat in future discussions. We experience an uncertainty about a topic that we don't know about. However, when we "receive" that uncertainty, it becomes information.
There is a subtle tradeoff between uncertainty and brainpower for a particular subject. You will start to notice this later in the course. Observe that when there is high uncertainty (e.g., a completely new topic), our brain exerts effort to study a material. Whenever we have low uncertainty (e.g., review a familiar subject), we exert less effort for the subject. The amount of brainpower that we use can be analogous to computing power. We associate uncertainty to the data that we need to process. This example shows where information theory and complexity mix together. If we are given a similar problem, what would be the best solution? Information theory does not tell us how to solve a problem because it is only a measurement. The solutions are up to us. Going back to our study example, if we need to study a completely new topic, what are our options? Do we spend so much time on the material to cover the bulk of it? How much brainpower do we use? Or can we cut the material into chunks so that we can process it with optimum speed and power? The solution is up to us. We just need to be creative.
Deriving Information
Shannon has a very nice comprehensive introduction on how he formulated his theory [2]. Let's try to summarize his approach in a different way [3]. Remember, our mathematical definition of information is the measurement of surprise. Let's say we have an experiment with two independent events and . Shannon pointed out important properties of information:
- should be a decreasing function of . The same goes for event .
- If the two events have then it should follow that . A more surprising event should have higher information.
- Since both events are independent, then . Also, following from the previous item: .
Let's look at a simple example. Suppose we'll be drawing a card from a pack of 52 casino cards. What is the probability when the drawn card is:
- A club. Let this be event .
- An ace. Let this be event .
- An ace of clubs. Let this be event .
The equivalent probabilities would be:
Since we know the probabilities and the desired properties for Shannon's theorem, we should observe the following: because it is more surprising to draw an ace compared to drawing any card that is a club. because it is a lot more surprising to get the ace of clubs compared to the individual events. Moreover, our intuition tells us that . The question is, what kind of function should information be if we know the probabilities of each event? After hours of thinking, Shannon came up with:
-
(1)
-
Which can also be re-written as the equation below because of the law of logarithms .
-
(1)
-
So either way works and we'll call them equation 1. Let's apply these in action, if we calculate the information for events , , and .
It satisfies everything we agreed upon!
It's simple and it agrees well. There's a special case say for some event . This leads to . This breaks those assumptions that Shannon made. Because of this we'll have to make an exemption where then . So equation 1 is more appropriately written as:
-
(1)
-
Bits, Bans, and Nats
You might wonder why we used base 2 for the log function. This is just for convenience because using the equation in base 2 suits well with our binary computations. The units of information if taken in base 2 are in bits. If taken in base 3 we call them trits. If taken in base 10 we call them bans, and if taken in base , we call them nats. The table below shows this comparison.
| base | units | |
|---|---|---|
| 2 | bits (from binary) | 2.00 |
| 3 | trits (from trinary) | 1.26 |
| nats (from natural logarithm) | 1.38 | |
| 10 | bans | 0.602 |
Information Examples
In summary, information can be thought of as the amount of surprise at seeing an event. Note that a highly probable outcome is not surprising. Consider the following events:
| Event | Probability | Information (Surprise) |
|---|---|---|
| Someone tells you . | ||
| You got the wrong answer on a 4-choice multiple choice question. | ||
| You guessed correctly on a 4-choice multiple choice question. | ||
| You got the correct answer in a True or False question. | ||
| You rolled a seven on rolling a pair of dice. | ||
| Winning the Ultra Lotto 6/58 jackpot. |
Entropy
Information is a measure of surprise for one event only. We can expand this to a collection of events encapsulated with some random variable . Recall that a random variable contains a set of outcomes and each outcome has an associated probability . Each outcome also has its own set of information . We can get the mean of all . We call this entropy which we denote with :
-
(2)
-
Entropy is just the mean of information for some random variable . Let's look at a few examples. Consider some random variable with outcomes . All outcomes have a probability of . What is ? Simple!
Therefore, the average information for the simple uniform distribution is bits. Let's take a look at another example. Suppose we flip a fair coin three times. Let the random variable be the sum of heads in those three flips. What is ? It's easier to tabulate the data.
Summing all terms we get:
Bounds of Entropy
Entropy has bounds, meaning there is a lower and upper limit to this value. Just like in any system, these bounds serve as limitations to our measurement. In a nutshell, for any random variable with outcomes, the bounds of entropy is:
-
(3)
-
The lower bound occurs if and only if one of the outcomes has absolute certainty (i.e., ). This is trivial. Recall that for a random variable with outcomes and their associated probabilities . The sum of all probabilities must sum up to 1. Such that:
If one of the elements has absolute certainty: then that means all other probabilities need to be where . Solving for if this happens.
The upper bound is a bit tricky. First we need to recognize a fact that with equality if and only if . When we say "with equality" then that means the equal sign holds true if and only if the condition is met. This is trivial: if and only if . We can also observe and from figure 1.
Second, we need to appreciate what Gibbs inequality tells us. Suppose we have two probability distributions and . Also note that and . Gibbs inequality says:
-
(4)
-
Simplifying the right handside results in:
In other words, Gibbs inequality says that:
-
(5)
-
If and only if for all . Take note of equation 5 and its condition for being true. We will use this result for deriving the upper bound. Now, let's consider a random variable with probability distribution . Let's find what kind of distribution maximizes the entropy function. We have:
The second step works because we know that . The last step works because of Gibbs inequality (i.e., ). Therefore works if and only if for all .
In plain English, this means that we attain maximum entropy if and only if all outcomes are equiprobable!
In summary, the bounds of entropy can be summarized as .
- The lower bound occurs if at least one outcome has absolute certainty .
- The upper bound occurs if all outcomes are equiprobable . Assuming there are outcomes.
Interpreting Entropy
There are several ways to interpret entropy. Here, we'll use binary trees as a graphical representation [4]. It's easier to appreciate a concept if we associate it to something. In the previous examples, we use bits as our units of information. Take note that our definition of bit is a definite amount of information. It is common to use bits because it suits the binary system which we will see in the succeeding discussions.
Suppose we're in a role-playing game where we have control of the ending of our hero. Let this be random variable which contains outcomes . There are alternate endings for our hero's story. The decision tree for our hero is shown in figure 3. For now, let's also assume that at every node, our hero can take the left or the right path with probabilities . Let's say the game designer made it this way such that the player experiences these paths. Since all then each ending is equiprobable and the entropy is bits of information.
Here's why bits is such a convenient unit for information. If we know the entropy then it also means we have equiprobable outcomes. In our example, since we know that the entropy is then that also translates to equiprobable outcomes. Keep this interpretation in mind. If we forget, we can always go back to this idea.
Now, suppose the game designer changed all the probabilities for each left and right path to spice up the game. Figure 4 shows a decision tree with varying probabilities per path.
The probabilities of each ending are:
Calculating the entropy would give us bits of information. Remember, we mentioned that given some we can think of it as having equiprobable outcomes. Of course, drawing 4.1 different outcomes is impossible with binary trees but let's approximate it to 4. What does this mean? If the distribution of the outcomes follows that of what is in figure 4, then having 8 outcomes for the ending is almost as good as having 4 equiprobable endings! This implies that if a thousand players (or more) play the game with the non-uniform distribution of endings, then it's as good as playing a game with only 4 endings. The catch is that we don't know those outcomes. It could be a direct combination of existing outcomes (e.g., ending a and b are combined), or a mixture of partitioned outcomes (e.g., a piece of ending h, g, and d can be combined together). Of course, the uniform distribution tree will be more exciting if all 8 outcomes are equiprobable. It's consistent because its entropy bits indicates that it is more surprising. The non-uniform distribution tree will be less exciting because it's effectively equivalent to 4 outcomes only. Wherein it's also consistent with its entropy because bits is less surprising compared to the uniform distribution.
In summary, one good interpretation of entropy is that if we are given bits of information (or uncertainty) then we are "effectively" looking at a system that has equiprobable outcomes.
A Dicey Example
Suppose you were to roll two fair 6-sided dies. Let the random variable be the sum of the two dies. Do the following:
(a) Tabulate the outcomes, the probability of each outcome, the information of each outcome.
(b) Calculate the entropy of .
(c) Interpret what it means to have bits of information for this experiment.
Solution
(a) The table below is the answer. We'll leave it up to you how the probabilities and information is computed.
| Outcome | (bits) | |
|---|---|---|
(b) Use equation 2 to solve for the entropy. It's written below for convenience.
bits of information.
(c) From the previous discussion, it appears that this experiment is equivalent to equiprobable outcomes. The 2 die rolls can be an equivalent binary tree system that produces 9.68 equiprobable outcomes. It can't really happen in reality but you get the idea. The entropy of the sum of two die rolls is more surprising than drawing any club in a deck of 52 casino cards (i.e., bits of information). It's a little less surprising than drawing any ace of cards (i.e., bits of information). It's much less surprising than drawing an ace of clubs (i.e., bits of information). Again, we emphasize that entropy and information are measures of uncertainty. Cool right?
Bernoulli Entropy
Often times, we prefer to write equations and use a computer to assist us in our analysis. Recall that a Bernoulli trial is an outcome with probability for getting a success. The probability is for failing. We usually use this for the coin toss problem. Let's define to be the entropy of a Bernoulli trial written as:
-
(6)
-
Writing the equation this way is convenient and easy for the reader. The first term on the right hand side is the component for getting a success while the second term is the component for getting a fail. You just need to program this (e.g., Python, MATLAB, or C) and you can plot how the entropy varies with changing . Figure 8 shows how the entropy changes with varying . Let's look at a few numbers:
- yields bits.
- yields bits.
- yields bits.
- yields bits.
- yields bits.
Observe that the entropy is symmetric. The entropy when we are likely to succeed is the same as we are likely to fail (e.g., and ). The highest entropy is when we are unsure of winning or failing (e.g., ).
References
- ↑ Sousa, David A. 2006. How the Brain Learns. Thousand Oaks, Calif: Corwin Press.
- ↑ Shannon, C. E., & Weaver, W., The mathematical theory of communication. Urbana: University of Illinois Press. 1949.
- ↑ Applebaum, D. , Probability and Information: An Integrated Approach, Cambridge University Press, 2008.
- ↑ Stone, J.V. , Information Theory: A Tutorial Introduction, Sebtel Press, 2015.