Joint entropy, conditional entropy, and mutual information

Joint Entropies

In this module, we'll discuss several extensions of entropy. Let's begin with joint entropy. Suppose we have a random variable $X$ with elements $\{x_{1},x_{2},...,x_{i},...,x_{n}\}$ and random variable $Y$ with elements $\{y_{1},y_{2},...,y_{j},...,y_{m}\}$. We define the joint entropy of $H(X,Y)$ as:

$H(X,Y)=-\sum _{i=1}^{n}\sum _{j=1}^{m}P(x_{i},y_{j})\log _{2}\left(P(x_{i},y_{j})\right)$

(1)

Take note that $H(X,Y)=H(Y,X)$. This is trivial. From our previous discussion about the decision trees of a game, we used joint entropies to calculate the overall entropy.

Conditional Entropies

There are two steps to understand conditional entropies. The first is the uncertainty of a random variable caused by a single outcome only. Suppose we have the same random variables $X$ and $Y$ defined earlier in joint entropies. Let's denote $P(y_{j}|x_{i})$ as the conditional probability of $y_{j}$ when event $x_{i}$ happened. We define the entropy $H(Y|x_{i})$ as the entropy of the random variable $Y$ given a $x_{i}$ happened. Take note that we're only interested in the entropy of $Y$ when only the outcome $x_{i}$ occurred. Mathematically this is:

$H(Y|x_{i})=-\sum _{j=1}^{m}P(y_{j}|x_{i})\log _{2}\left(P(y_{j}|x_{i})\right)$

(2)

Just to repeat because it may be confusing, equation 2 just pertains to the uncertainty when only a single event happened. We can extend this to the total entropy $Y$ when any of the outcomes in $X$ happens. If we treat $H(Y|\cdot )$ contains a range of $\{H(Y|x_{1}),H(Y|x_{2}),H(Y|x_{3}),...,H(Y|x_{n})\}$ and the probability distribution for each associated $H(Y|x_{i})$ is $\{P(x_{1}),P(x_{2}),P(x_{3}),...P(x_{n})\}$ so that $H(Y|\cdot )$ is a function of $X$. Then we define $H(Y|X)$ as the conditional probability of $Y$ given $X$ as:

$H(Y|X)=E(H(Y|\cdot ))=-\sum _{j=1}^{m}P(x_{i})H(Y|x_{i})$

(3)

Substituting equation 2 to equation 3 and knowing that $P(y_{j}|x_{i})P(x_{i})=P(x_{i},y_{j})$. We can re-write this as:

$H(Y|X)=-\sum _{i=1}^{n}\sum _{j=1}^{m}P(x_{i},y_{j})\log _{2}(P(y_{j}|x_{i}))$

(3)

Note that it is trivial to prove that $H(Y|X)=H(Y)$ if $Y$ and $X$ are independent. We'll leave it up to you to prove this. A few hints include: $P(y_{j}|x_{i})=P(y_{j})$ and $P(y_{j},x_{i})=P(x_{i})P(y_{j})$ if $Y$ and $X$ are independent.

Binary Tree Example

Figure 1: Binary tree example.

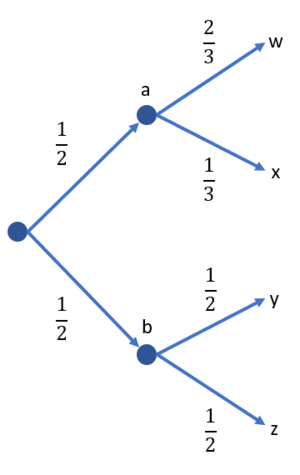
Let's apply the first two concepts in a simple binary tree example. Suppose we let $X$ be a random variable with outcomes $\{a,b\}$ and probabilities $\{P(a)=P(b)={\frac {1}{2}}\}$. Let $Y$ be the random variable with outcomes $\{w,x,y,z\}$. We are also given the probabilities $P(w|a)={\frac {2}{3}}$, $P(x|a)={\frac {1}{3}}$, $P(y|b)={\frac {1}{2}}$, and $P(z|b)={\frac {1}{2}}$. Figure 1 shows the binary tree. Calculate:

(a) $H(Y|a)$

(b) $H(Y|b)$

(c) $H(Y|X)$

(d) $H(X,Y)$

Solution

(a) Use equation 2 to solve $H(Y|a)$

${\begin{aligned}H(Y|a)&=-P(w|a)\log _{2}(P(w|a))-P(x|a)\log _{2}(P(x|a))\\&=-{\frac {2}{3}}\log _{2}({\frac {2}{3}})-{\frac {1}{3}}\log _{2}({\frac {1}{3}})\\&=0.918\ {\textrm {bits}}\end{aligned}}$

(b) Same as in (a), use equation 2 to solve $H(Y|b)$

${\begin{aligned}H(Y|b)&=-P(y|b)\log _{2}(P(y|b))-P(z|b)\log _{2}(P(z|b))\\&=-{\frac {1}{2}}\log _{2}({\frac {1}{2}})-{\frac {1}{2}}\log _{2}({\frac {1}{2}})\\&=1.000\ {\textrm {bits}}\end{aligned}}$

(c) Can be solved in two ways. First is to use equation 3.

${\begin{aligned}H(Y|X)&=E(H(Y|\cdot ))\\&=P(a)H(Y|a)+P(b)H(Y|b)\\&={\frac {1}{2}}(0.918)+{\frac {1}{2}}(1.000)\\&=0.959\ {\textrm {bits}}\end{aligned}}$

Or, we can solve it using the alternative version of equation 3. But we also need to know the joint probabilities:

• $P(a,w)={\frac {1}{3}}$
• $P(a,x)={\frac {1}{6}}$
• $P(b,y)={\frac {1}{4}}$
• $P(b,z)={\frac {1}{4}}$

${\begin{aligned}H(Y|X)&=-\sum _{i=1}^{n}\sum _{j=1}^{m}P(x_{i},y_{j})\log _{2}(P(y_{j}|x_{i}))\\&=-P(a,w)\log _{2}(P(a|w))-P(a,x)\log _{2}(P(a|x))-P(b,y)\log _{2}(P(b|y))-P(b,z)\log _{2}(P(b|z))\\&=-{\frac {1}{3}}\log _{2}\left({\frac {2}{3}}\right)-{\frac {1}{6}}\log _{2}\left({\frac {1}{3}}\right)-{\frac {1}{4}}\log _{2}\left({\frac {1}{2}}\right)-{\frac {1}{4}}\log _{2}\left({\frac {1}{2}}\right)\\&=0.959\ {\textrm {bits}}\end{aligned}}$

(d) We already listed the joint probabilities in (c). We simply use equation 1 for this:

${\begin{aligned}H(X,Y)&=-\sum _{i=1}^{n}\sum _{j=1}^{m}P(x_{i},y_{j})\log _{2}\left(P(x_{i},y_{j})\right)\\&=-P(a,w)\log _{2}(P(a,w))-P(a,x)\log _{2}(P(a,x))-P(b,y)\log _{2}(P(b,y))-P(b,z)\log _{2}(P(b,z))\\&=-{\frac {1}{3}}\log _{2}\left({\frac {1}{3}}\right)-{\frac {1}{6}}\log _{2}\left({\frac {1}{6}}\right)-{\frac {1}{4}}\log _{2}\left({\frac {1}{4}}\right)-{\frac {1}{4}}\log _{2}\left({\frac {1}{4}}\right)\\&=1.959\ {\textrm {bits}}\end{aligned}}$

Important Note!

This example actually shows us an important observation:

$H(X,Y)=H(X)+H(Y|X)$

(4)

We can easily observe that this holds true for the binary tree example. This has an important interpretation: The combined uncertainty in $X$ and $Y$ (i.e., $H(X,Y)$) is the sum of that uncertainty which is totally due to $X$ (i.e., $H(X)$), and that which is still due to $Y$ once $X$ has been accounted for (i.e., $H(Y|X)$).

Since $H(X,Y)=H(Y,X)$ it also follows that:

$H(Y,X)=H(Y)+H(X|Y)$

(5)

If $X$ and $Y$ are independent the:

$H(X,Y)=H(X)+H(Y)$

(6)

An alternative interpretation to $H(Y|X)$ is the information content of $Y$ which is NOT contained in $X$.

Mutual Information

With the final discussion on the properties of joint and conditional entropies, we also define mutual information as the information content of $Y$ contained within $X$ written as:

$I(X,Y)=H(Y)-H(Y|X)$

(6)

Or:

$I(X,Y)=H(X)-H(X|Y)$

(6)

If we plug in the definitions of entropy and conditional entropy, mutual information in expanded form is:

$I(X,Y)=\sum _{i=1}^{n}\sum _{j=1}^{m}P(x_{i},y_{j})\log _{2}\left({\frac {P(x_{i},y_{j})}{P(x_{i})P(y_{j})}}\right)$

(7)

It also follows that:

• $I(X,Y)=I(Y,X)$. This is trivial from equation 7.
• If $X$ and $Y$ are independent, then $I(X,Y)=0$. This is also trivial from equation 7.

As a short example, we can use the binary tree problem again. Let's compute $I(X,Y)$. We simply need to use equation 6: $I(X,Y)=H(Y)-H(Y|X)$. We already know $H(Y|X)=0.959$ bits. $H(Y)$ is computed by first knowing $\{P(w),P(x),P(y),P(z)\}$. Recall that:

$P(y_{j})=\sum _{i=1}^{n}P(y_{j}|x_{i})P(x_{i})$

But then, for each outcome in $Y$ has the same probability of the joint entropy. For example, event $w$ only occurs if event $a$ occurred first. Event $x$ occurs only if event $b$ occurred first. So it means that:

• $P(w)=P(w|a)P(a)=P(w,a)={\frac {1}{3}}$
• $P(x)=P(x|a)P(a)=P(x,a)={\frac {1}{6}}$
• $P(y)=P(y|b)P(b)=P(y,b)={\frac {1}{4}}$
• $P(z)=P(z|b)P(b)=P(z,b)={\frac {1}{4}}$

Therefore, $H(Y)=H(X,Y)=1.959$ bits. Therefore, the information $I(X,Y)=H(Y)-H(Y|X)=1.959-0.959=1.000$ bits.