Difference between revisions of "Channel polarization"
Adrian Vidal (talk | contribs) |
Adrian Vidal (talk | contribs) |
||
| (28 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | In 2007, Erdal Arikan discovered a practical channel coding scheme that achieves the capacity of binary-input discrete memoryless channels. His method relies on a phenomenon now known as ''channel polarization''. First, we observe that achieving the capacity of the following channels with input <math>X</math> and output <math>Y</math> is straightforward: | ||
| + | * channels where <math>X</math> and <math>Y</math> are one-to-one functions of each other, and | ||
| + | * channels where <math>X</math> is independent of <math>Y</math>. | ||
| + | |||
| + | The first class of channels is ''perfect'' in the sense that we do not need to introduce any redundancy to transmit <math>X</math> reliably. In other words, uncoded transmission will suffice. To transmit, five symbols from the source alphabet <math>\mathcal{X}</math>, we simply pass the five symbols over the channel. Since there is one-to-one correspondence between the input and output alphabets, it is always possible to recover <math>X</math> without errors. | ||
| + | |||
| + | The second class of channels is ''useless'' in the sense that no matter how much redundancy we add, the channel output will not tell us anything about the input. Since the input and output rvs are independent, <math>I(X;Y)=0</math> and to achieve capacity, we simply '''not''' use the channel. (In practice, we can transmit a fixed symbol every time since there is no information if the transmission is not random at all.) | ||
| + | |||
== Synthetic channels == | == Synthetic channels == | ||
| + | |||
| + | Most other classes fall in the wide space between perfect channels and useless channels. Through a simple operation, we can repeatedly "polarize" a channel so that it ends up as either a near-perfect channel or a near-useless channel. | ||
| + | |||
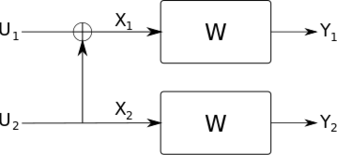
| + | Let <math>W: X \rightarrow Y</math> be a binary-input channel with input alphabet <math>\mathcal{X} = \{0,1\}</math>, and let <math>I(W)</math> be the mutual information between <math>X</math> and <math>Y</math> assuming that <math>X</math> is uniformly distributed. In other works, this quantity is referred to as the ''symmetric capacity''. We construct two channels <math>W^-</math> and <math>W^+</math> schematically as shown below: | ||
| + | |||
| + | [[File:Polar transform.svg]] | ||
| + | |||
| + | <math>W^-</math> maps the input <math>U_1</math> to the tuple <math>(Y_1,Y_2)</math> while <math>W^+</math> maps <math>U_2</math> to the tuple <math>(U_1,Y_1,Y_2)</math>. Since <math>U_2</math> interferes with <math>U_1</math>, we have <math>I(W^-) \le I(W)</math>, and since <math>W^+</math> contains extra information about the input (<math>U_1</math>), <math>I(W^+) \ge I(W)</math>. In general, it can be shown that | ||
| + | |||
| + | <math>I(W) = \frac{I(W^-) + I(W^+)}{2},</math> | ||
| + | |||
| + | where <math>I(W^-) = I(U_1; Y_1,Y_2)</math> and <math>I(W^+) = I(U_2; U_1, Y_1, Y_2)</math>. | ||
| + | |||
| + | == Binary symmetric channel == | ||
| + | Let <math>p</math> be the crossover probability of a binary symmetric channel (BSC). | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | colspan='2' rowspan='2'| | ||
| + | | colspan='4' style="text-align: center;"| <math>(Y_1, Y_2)</math> | ||
| + | |- | ||
| + | | 00 | ||
| + | | 01 | ||
| + | | 10 | ||
| + | | 11 | ||
| + | |- | ||
| + | | rowspan='4' | <math>(U_1,U_2)</math> | ||
| + | | 00 | ||
| + | | <math>(1-p)^2</math> | ||
| + | | <math>p(1-p)</math> | ||
| + | | <math>p(1-p)</math> | ||
| + | | <math>p^2</math> | ||
| + | |- | ||
| + | | 01 | ||
| + | | <math>p^2</math> | ||
| + | | <math>p(1-p)</math> | ||
| + | | <math>p(1-p)</math> | ||
| + | | <math>(1-p)^2</math> | ||
| + | |- | ||
| + | | 10 | ||
| + | | <math>p(1-p)</math> | ||
| + | | <math>p^2</math> | ||
| + | | <math>(1-p)^2</math> | ||
| + | | <math>p(1-p)</math> | ||
| + | |- | ||
| + | | 11 | ||
| + | | <math>p(1-p)</math> | ||
| + | | <math>(1-p)^2</math> | ||
| + | | <math>1-p^2</math> | ||
| + | | <math>p(1-p)</math> | ||
| + | |- | ||
| + | |} | ||
| + | |||
| + | In this section, we produce the channel matrices corresponding to <math>W^-: U_1 \rightarrow (Y_1, Y_2)</math> and <math>W^+: U_2 \rightarrow (U_1, Y_1, Y_2)</math>. Recall at the channel matrices give the conditional probabilities of the outputs given the input. For <math>W^-</math>, we have | ||
| + | |||
| + | <math>p(Y_1,Y_2|U_1) = p(U_2=0)p(Y_1,Y_2|U_1, U_2=0) + p(U_2=1)p(Y_1,Y_2|U_1, U_2=1) = \frac{1}{2}(p(Y_1,Y_2|U_1, U_2=0) + p(Y_1,Y_2|U_1, U_2=1)) </math> | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | colspan='2' rowspan='2'| | ||
| + | | colspan='4' style="text-align: center;"| <math>(Y_1, Y_2)</math> | ||
| + | |- | ||
| + | | 00 | ||
| + | | 01 | ||
| + | | 10 | ||
| + | | 11 | ||
| + | |- | ||
| + | | rowspan='4' | <math>U_1</math> | ||
| + | | 0 | ||
| + | | <math>0.5(1-2p+2p^2)</math> | ||
| + | | <math>p(1-p)</math> | ||
| + | | <math>p(1-p)</math> | ||
| + | | <math>0.5(1-2p+2p^2)</math> | ||
| + | |- | ||
| + | | 1 | ||
| + | | <math>p(1-p)</math> | ||
| + | | <math>0.5(1-2p+2p^2)</math> | ||
| + | | <math>0.5(1-2p+2p^2)</math> | ||
| + | | <math>p(1-p)</math> | ||
| + | |- | ||
| + | |} | ||
| + | |||
| + | {{Note|Checkpoint: Verify that each row of the table for <math>W^-: U_1 \rightarrow (Y_1, Y_2)</math> sum to 1.|reminder}} | ||
| + | |||
| + | It turns out that the channel <math>W^{-}: U_1 \rightarrow (Y_1, Y_2)</math> reduces to another BSC. To see this, consider the case where <math>(Y_1, Y_2) = (0,0)</math>. To minimize the error probability, we must decide the value of <math>U_1</math> that has the greater likelihood. For <math>0 < p < 0.5</math>, <math> 0.5(1-2p+2p^2) > p(1-p)</math> so that the maximum-likelihood (ML) decision is <math>U_1 = 0</math>. Using the same argument, we see that the ML decision is <math>U_1 = 0</math> for <math>(Y_1,Y_2)=(1,1)</math>. More generally, the receiver decision is to set <math>\hat{U_1} = Y_1 \oplus Y_2</math>. Indeed, if the crossover probability is low, it is very likely that <math>Y_1 = U_2 \oplus U_1</math> and <math>Y_2 = U_2</math>. Solving for <math>U_2</math> and plugging it back produces the desired result. | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | colspan='2' rowspan='2'| | ||
| + | | colspan='4' style="text-align: center;"| <math>(Y_1, Y_2)</math> | ||
| + | |- | ||
| + | | 00,11 | ||
| + | | 01,10 | ||
| + | |- | ||
| + | | rowspan='2'| <math>U_1</math> | ||
| + | | 00 | ||
| + | | <math>1-2p+2p^2</math> | ||
| + | | <math>2p(1-p)</math> | ||
| + | |- | ||
| + | | 01 | ||
| + | | <math>2p(1-p)</math> | ||
| + | | <math>1-2p+2p^2</math> | ||
| + | |- | ||
| + | |} | ||
| + | |||
| + | We just saw that despite having a quartenary output alphabet, <math>W^{-}</math> is equivalent to a BSC. To get the effective crossover probability of this synthetic channel, we just determine the probability that the ML decision <math>\hat{U_1}</math> is not the same as <math>U_1</math>. This will happen with probability <math>2p(1-p)</math>. Intuitively, <math>W^{-}</math> should have less mutual information compared to the original channel <math>W</math> since an independent source <math>U_2</math> interferes with <math>U_1</math> on top of the effects of the BSC. For example, if <math>p=0.1</math> for the original BSC, then the crossover probability of <math>W^-</math> is <math>2p(1-p) = 0.18</math>, which is worse than the original. It also has the intuitive property that it cannot make the ''worst'' possible BSC any worse: if the original BSC had <math>p=1/2</math>, then <math>W^-</math> would have the same crossover probability. | ||
| + | |||
| + | {{Note|Checkpoint: Show that for <math>0 < p < 1/2</math>, <math>p < 2p(1-p)</math>.|reminder}} | ||
| + | |||
| + | Now, let us consider the other synthetic channel <math>W^{+}: U_2 \rightarrow (U_1, Y_1, Y_2)</math>. This synthetic channel has a greater mutual information compared to the original BSC due to the "stolen" information about <math>U_1</math>. As with the previous synthetic channel, we can produce the transition probability matrix from <math>U_2</math> to <math>(U_1, Y_1, Y_2)</math>, which now has an eight-element output alphabet. To facilitate the discussion, the columns of the table below have been grouped according to their entries: | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | colspan='2' rowspan='2'| | ||
| + | | colspan='8' style="text-align: center;"| <math>(U_1,Y_1, Y_2)</math> | ||
| + | |- | ||
| + | | 000 | ||
| + | | 110 | ||
| + | | 001 | ||
| + | | 010 | ||
| + | | 100 | ||
| + | | 111 | ||
| + | | 011 | ||
| + | | 101 | ||
| + | |- | ||
| + | | rowspan='2'| <math>U_2</math> | ||
| + | | 0 | ||
| + | | <math>0.5(1-p)^2</math> | ||
| + | | <math>0.5(1-p)^2</math> | ||
| + | | <math>0.5p(1-p)</math> | ||
| + | | <math>0.5p(1-p)</math> | ||
| + | | <math>0.5p(1-p)</math> | ||
| + | | <math>0.5p(1-p)</math> | ||
| + | | <math>0.5p^2</math> | ||
| + | | <math>0.5p^2</math> | ||
| + | |- | ||
| + | | 1 | ||
| + | | <math>0.5p^2</math> | ||
| + | | <math>0.5p^2</math> | ||
| + | | <math>0.5p(1-p)</math> | ||
| + | | <math>0.5p(1-p)</math> | ||
| + | | <math>0.5p(1-p)</math> | ||
| + | | <math>0.5p(1-p)</math> | ||
| + | | <math>0.5(1-p)^2</math> | ||
| + | | <math>0.5(1-p)^2</math> | ||
| + | |- | ||
| + | |} | ||
| + | |||
| + | In the transition probability matrix, we see that there are four columns where the receiver will not be able to tell whether <math>U_2 = 0</math> or <math>U_2 = 1</math>. We can call such a scenario an ''erasure'', and say that the transmitted bit is erased with probability <math>4\times 0.5p(1-p) = 2p(1-p)</math>. Clearly, we cannot reduce this synthetic channel to a BSC since there are no erasures in a BSC. Regardless, we can still come up the following more manageable reduction: | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | colspan='2' rowspan='2'| | ||
| + | | colspan='8' style="text-align: center;"| <math>(U_1,Y_1, Y_2)</math> | ||
| + | |- | ||
| + | | 000,110 | ||
| + | | 001,010,100,111 | ||
| + | | 011,101 | ||
| + | |- | ||
| + | | rowspan='2' | <math>U_2</math> | ||
| + | | 0 | ||
| + | | <math>(1-p)^2</math> | ||
| + | | <math>2p(1-p)</math> | ||
| + | | <math>p^2</math> | ||
| + | |- | ||
| + | | 1 | ||
| + | | <math>p^2</math> | ||
| + | | <math>2p(1-p)</math> | ||
| + | | <math>(1-p)^2</math> | ||
| + | |- | ||
| + | |} | ||
| + | |||
| + | {{Note|Checkpoint: Show that the mutual information is preserved after the reduction.|reminder}} | ||
== Binary erasure channel == | == Binary erasure channel == | ||
| − | Let <math>\epsilon</math> be the erasure probability of a binary erasure channel (BEC). | + | Let <math>\epsilon</math> be the erasure probability of a binary erasure channel (BEC). As with the BSC, we can start with the conditional probability of <math>(Y_1, Y_2)</math> given <math>(U_1,U_2)</math>. |
| + | |||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| − | | | + | | colspan='2' rowspan='2'| |
| + | | colspan='9' style="text-align: center;"| <math>(Y_1, Y_2)</math> | ||
| + | |- | ||
| 00 | | 00 | ||
| 0? | | 0? | ||
| Line 16: | Line 200: | ||
| 11 | | 11 | ||
|- | |- | ||
| + | | rowspan='4' | <math>(U_1, U_2)</math> | ||
| 00 | | 00 | ||
| <math>(1 - \epsilon)^2</math> | | <math>(1 - \epsilon)^2</math> | ||
| Line 62: | Line 247: | ||
|} | |} | ||
| + | The synthetic channel <math>W^{-}: U_1 \rightarrow (Y_1,Y_2)</math> can be obtained by marginalizing <math>U_2</math>, | ||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| − | | | + | | colspan='2' rowspan='2'| |
| + | | colspan='9' style="text-align: center;"| <math>(Y_1, Y_2)</math> | ||
| + | |- | ||
| 00 | | 00 | ||
| 0? | | 0? | ||
| Line 75: | Line 263: | ||
| 11 | | 11 | ||
|- | |- | ||
| + | | rowspan='2' | <math>U_1</math> | ||
| 0 | | 0 | ||
| <math>0.5(1 - \epsilon)^2</math> | | <math>0.5(1 - \epsilon)^2</math> | ||
| Line 99: | Line 288: | ||
|} | |} | ||
| − | == | + | A maximum-likelihood receiver will decide that <math>U_1 = 0</math> if is more likely than <math>U_1 = 0</math>. If there are ties, we declare an erasure, denoted by <math>?</math>. This allows us to reduce the nine-element output alphabet into three groups. The receiver declares that <math>\hat{U}_1 = 0</math> if <math>Y_1 \oplus Y_2 = 0</math> and <math>\hat{U}_1 = 1</math> if if <math>Y_1 \oplus Y_2 = 1</math>. This is very similar to the XOR decisions in our discussion of the BSC. The difference now is that several combinations may correspond to an erasure. From the table below, it can be seen that <math>W^-</math> is equivalent to a BEC with erasure probability of <math>2\epsilon - \epsilon^2</math>. |
| − | |||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| − | | | + | | colspan='2' rowspan='2'| |
| − | + | | colspan='3' style="text-align: center;"| <math>(Y_1, Y_2)</math> | |
| − | | | ||
| − | | | ||
| − | | | ||
|- | |- | ||
| − | | 00 | + | | 00,11 |
| − | | | + | | 0?,?0,??,?1,1? |
| − | + | | 01,11 | |
| − | |||
| − | | | ||
|- | |- | ||
| − | | | + | | rowspan='2' | <math>U_1</math> |
| − | | <math> | + | | 0 |
| − | | | + | | <math>(1 - \epsilon)^2</math> |
| − | | <math> | + | | <math>2\epsilon - \epsilon^2</math> |
| − | | <math> | + | | |
|- | |- | ||
| − | | | + | | 1 |
| − | | | + | | |
| − | | <math> | + | | <math>2\epsilon - \epsilon^2</math> |
| − | + | | <math>(1 - \epsilon)^2</math> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | | <math>(1- | ||
| − | |||
| − | |||
|- | |- | ||
|} | |} | ||
| + | |||
| + | The other synthetic channel <math>W^+: U_2 \rightarrow (U_1, Y_1, Y_2)</math> has an output alphabet of size 18. For brevity, the table below shows the reduced transition probability matrix. Upon inspection, we see that the reduced channel is equivalent to another BEC with erasure probability <math>\epsilon^2</math>. For all <math>0 < \epsilon < 1</math>, <math>\epsilon^2 < 2\epsilon - \epsilon^2</math> which guarantees that <math>W^{+}</math> has higher mutual information compared to <math>W^-</math>. | ||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| − | | | + | | colspan='2' rowspan='2'| |
| − | | 00 | + | | colspan='3' style="text-align: center;"| <math>(U_1,Y_1, Y_2)</math> |
| − | | | + | |- |
| − | | 10 | + | | 000, 00?, 0?0, 1?0, 110, 11? |
| − | + | | 0??, 1?? | |
| + | | 0?1, 01?, 011, 10?, 101, 1?1 | ||
|- | |- | ||
| − | | | + | | rowspan='2' | <math>U_2</math> |
| − | | <math> | + | | 0 |
| − | | <math> | + | | style="text-align: center;" | <math>1 - \epsilon^2</math> |
| − | | | + | | style="text-align: center;" | <math>\epsilon^2</math> |
| − | | <math> | + | | |
|- | |- | ||
| − | | | + | | 1 |
| − | | | + | | |
| − | | <math> | + | | style="text-align: center;" | <math>\epsilon^2</math> |
| − | | <math> | + | | style="text-align: center;" | <math>1 - \epsilon^2</math> |
| − | |||
|- | |- | ||
|} | |} | ||
| − | + | Finally, observe that the capacity of the original BEC is <math>C(W) = 1 - \epsilon</math>. Since <math>W^{-}</math> and <math>W^{+}</math> are also BECs, then their capacities are given by similar expressions. Adding the capacities of the synthetic channels gives twice the capacity of the original channel, | |
| + | |||
| + | <math>(1 - \epsilon^2) + (1 - 2\epsilon + \epsilon^2) = 2 - 2 \epsilon = 2 ( 1 - \epsilon)</math> | ||
| + | |||
| + | {{Note|Checkpoint: Verify that <math>W^+</math> can be decoded as follows: | ||
| + | * If <math>U_1\oplus Y_1 = 0</math> or <math>Y_2 = 0</math>, output <math>\hat{U}_2 = 0</math>. | ||
| + | * If <math>U_1\oplus Y_1 = 1</math> or <math>Y_2 = 1</math>, output <math>\hat{U}_2 = 1</math>. | ||
| + | * Otherwise, declare an erasure. | ||
| + | |reminder}} | ||
| − | We | + | == Achieving capacity == |
| + | We can repeat the polar transform <math>n</math> times to produce <math>2^n</math> synthetic channels. For binary-input DMCs, it has been shown that for large <math>n</math>, around <math>2^n \cdot I(W)</math> of these <math>2^n</math> will be close to perfect and that around <math>2^n \cdot (1 - I(W))</math> will be close to useless. Thus, we have a practical encoder-decoder system: | ||
| + | * Produce <math>2^n</math> synthetic channels. | ||
| + | * Transmit i.i.d binary inputs <math>X</math> to each of the near-perfect channels. | ||
| + | * Transmit fixed bits (usually zero) as inputs to the near-useless channels. | ||
| + | * Perform successive-cancellation decoding at the receiver. | ||
| − | + | The binary erasure channel is easy to play with since we know that all synthetic channels are effectively BECs. Recall that if the parent BEC has erasure probability <math>\epsilon</math>, then the two synthetic channels it can generate have erasure probabilities <math>\epsilon^- = 2\epsilon - \epsilon^2</math> and <math> \epsilon^+ = \epsilon^2</math>. Here, <math>\epsilon^-</math> corresponds to the erasure due to the worse synthetic channel <math>W^-</math> and <math>\epsilon^+</math> corresponds to the better synthetic channel <math>W^+</math>. | |
| − | + | We can recursively apply the mapping <math>\epsilon \mapsto (2\epsilon-\epsilon^2, \epsilon^2) </math> to produce <math>2^n</math> erasure probabilities. For large <math>n</math>, around <math>\epsilon\cdot 2^n</math> of these values will be close to one (which means that the transmitted symbols are completely erased!), while almost all of the rest will have erasure probabilities close to zero (which means that the channel is almost noiseless). Module 5 is a small preview for you to see that the erasure probabilities indeed polarize for large <math>n</math>. Arikan's polarization result is non-trivial and requires proof techniques beyond what we can cover in CoE 161. | |
Latest revision as of 12:57, 7 May 2021
In 2007, Erdal Arikan discovered a practical channel coding scheme that achieves the capacity of binary-input discrete memoryless channels. His method relies on a phenomenon now known as channel polarization. First, we observe that achieving the capacity of the following channels with input and output is straightforward:
- channels where and are one-to-one functions of each other, and
- channels where is independent of .
The first class of channels is perfect in the sense that we do not need to introduce any redundancy to transmit reliably. In other words, uncoded transmission will suffice. To transmit, five symbols from the source alphabet , we simply pass the five symbols over the channel. Since there is one-to-one correspondence between the input and output alphabets, it is always possible to recover without errors.
The second class of channels is useless in the sense that no matter how much redundancy we add, the channel output will not tell us anything about the input. Since the input and output rvs are independent, and to achieve capacity, we simply not use the channel. (In practice, we can transmit a fixed symbol every time since there is no information if the transmission is not random at all.)
Contents
Synthetic channels
Most other classes fall in the wide space between perfect channels and useless channels. Through a simple operation, we can repeatedly "polarize" a channel so that it ends up as either a near-perfect channel or a near-useless channel.
Let be a binary-input channel with input alphabet , and let be the mutual information between and assuming that is uniformly distributed. In other works, this quantity is referred to as the symmetric capacity. We construct two channels and schematically as shown below:
maps the input to the tuple while maps to the tuple . Since interferes with , we have , and since contains extra information about the input (), . In general, it can be shown that
where and .
Binary symmetric channel
Let be the crossover probability of a binary symmetric channel (BSC).
| 00 | 01 | 10 | 11 | ||
| 00 | |||||
| 01 | |||||
| 10 | |||||
| 11 | |||||
In this section, we produce the channel matrices corresponding to and . Recall at the channel matrices give the conditional probabilities of the outputs given the input. For , we have
| 00 | 01 | 10 | 11 | ||
| 0 | |||||
| 1 | |||||
It turns out that the channel reduces to another BSC. To see this, consider the case where . To minimize the error probability, we must decide the value of that has the greater likelihood. For , so that the maximum-likelihood (ML) decision is . Using the same argument, we see that the ML decision is for . More generally, the receiver decision is to set . Indeed, if the crossover probability is low, it is very likely that and . Solving for and plugging it back produces the desired result.
| 00,11 | 01,10 | ||||
| 00 | |||||
| 01 | |||||
We just saw that despite having a quartenary output alphabet, is equivalent to a BSC. To get the effective crossover probability of this synthetic channel, we just determine the probability that the ML decision is not the same as . This will happen with probability . Intuitively, should have less mutual information compared to the original channel since an independent source interferes with on top of the effects of the BSC. For example, if for the original BSC, then the crossover probability of is , which is worse than the original. It also has the intuitive property that it cannot make the worst possible BSC any worse: if the original BSC had , then would have the same crossover probability.
Now, let us consider the other synthetic channel . This synthetic channel has a greater mutual information compared to the original BSC due to the "stolen" information about . As with the previous synthetic channel, we can produce the transition probability matrix from to , which now has an eight-element output alphabet. To facilitate the discussion, the columns of the table below have been grouped according to their entries:
| 000 | 110 | 001 | 010 | 100 | 111 | 011 | 101 | ||
| 0 | |||||||||
| 1 | |||||||||
In the transition probability matrix, we see that there are four columns where the receiver will not be able to tell whether or . We can call such a scenario an erasure, and say that the transmitted bit is erased with probability . Clearly, we cannot reduce this synthetic channel to a BSC since there are no erasures in a BSC. Regardless, we can still come up the following more manageable reduction:
| 000,110 | 001,010,100,111 | 011,101 | |||||||
| 0 | |||||||||
| 1 | |||||||||
Binary erasure channel
Let be the erasure probability of a binary erasure channel (BEC). As with the BSC, we can start with the conditional probability of given .
| 00 | 0? | 01 | ?0 | ?? | ?1 | 10 | 1? | 11 | ||
| 00 | ||||||||||
| 01 | ||||||||||
| 10 | ||||||||||
| 11 | ||||||||||
The synthetic channel can be obtained by marginalizing ,
| 00 | 0? | 01 | ?0 | ?? | ?1 | 10 | 1? | 11 | ||
| 0 | ||||||||||
| 1 | ||||||||||
A maximum-likelihood receiver will decide that if is more likely than . If there are ties, we declare an erasure, denoted by . This allows us to reduce the nine-element output alphabet into three groups. The receiver declares that if and if if . This is very similar to the XOR decisions in our discussion of the BSC. The difference now is that several combinations may correspond to an erasure. From the table below, it can be seen that is equivalent to a BEC with erasure probability of .
| 00,11 | 0?,?0,??,?1,1? | 01,11 | ||
| 0 | ||||
| 1 | ||||
The other synthetic channel has an output alphabet of size 18. For brevity, the table below shows the reduced transition probability matrix. Upon inspection, we see that the reduced channel is equivalent to another BEC with erasure probability . For all , which guarantees that has higher mutual information compared to .
| 000, 00?, 0?0, 1?0, 110, 11? | 0??, 1?? | 0?1, 01?, 011, 10?, 101, 1?1 | ||
| 0 | ||||
| 1 | ||||
Finally, observe that the capacity of the original BEC is . Since and are also BECs, then their capacities are given by similar expressions. Adding the capacities of the synthetic channels gives twice the capacity of the original channel,
- If or , output .
- If or , output .
- Otherwise, declare an erasure.
Achieving capacity
We can repeat the polar transform times to produce synthetic channels. For binary-input DMCs, it has been shown that for large , around of these will be close to perfect and that around will be close to useless. Thus, we have a practical encoder-decoder system:
- Produce synthetic channels.
- Transmit i.i.d binary inputs to each of the near-perfect channels.
- Transmit fixed bits (usually zero) as inputs to the near-useless channels.
- Perform successive-cancellation decoding at the receiver.
The binary erasure channel is easy to play with since we know that all synthetic channels are effectively BECs. Recall that if the parent BEC has erasure probability , then the two synthetic channels it can generate have erasure probabilities and . Here, corresponds to the erasure due to the worse synthetic channel and corresponds to the better synthetic channel .
We can recursively apply the mapping to produce erasure probabilities. For large , around of these values will be close to one (which means that the transmitted symbols are completely erased!), while almost all of the rest will have erasure probabilities close to zero (which means that the channel is almost noiseless). Module 5 is a small preview for you to see that the erasure probabilities indeed polarize for large . Arikan's polarization result is non-trivial and requires proof techniques beyond what we can cover in CoE 161.