Difference between revisions of "Conditional Entropy and Mutual Information"
Adrian Vidal (talk | contribs) (Created page with "When we work with multiple information sources (random variables) <math>X</math> and <math>Y</math>, the following details are useful: * How much information overlap is there...") |
Adrian Vidal (talk | contribs) |
||
| Line 15: | Line 15: | ||
<math>H(X|Y) = -\sum_{x\in \mathcal{X}}\sum_{y\in\mathcal{Y}} p(x,y) \log p(x|y)</math> | <math>H(X|Y) = -\sum_{x\in \mathcal{X}}\sum_{y\in\mathcal{Y}} p(x,y) \log p(x|y)</math> | ||
| − | + | Observe that the fraction in the definition of <math>I(X;Y)</math> consists of (1) the joint distribution <math>p(x,y)</math>, and (2) the product of marginal distributions <math>p(x)p(y)</math>. <math>I(X; Y)</math> is a measure of how far <math>X</math> and <math>Y</math> is from being independent, in which case <math>p(x,y) = p(x)p(y)</math> and the entire summation vanishes since <math> \log 1 = 0</math>. In our discussions, we simplify the notation so that <math>p(x,y)</math> and <math>p(y,x)</math> both refer to the probability that <math>X=x,Y=y</math>. With this remark, <math>I(X;Y) = I(Y; X)</math>. However, conditional entropy is not symmetric, i.e. in general <math>H(X|Y)</math> is not equal to <math>H(Y|X)</math>. | |
When <math>X</math> and <math>Y</math> are independent, all conditional probabilities <math>p(x|y)</math> reduces to <math>p(x)</math>, i.e., conditioning on <math>Y</math> does not change the probability of <math>X</math>. Hence, | When <math>X</math> and <math>Y</math> are independent, all conditional probabilities <math>p(x|y)</math> reduces to <math>p(x)</math>, i.e., conditioning on <math>Y</math> does not change the probability of <math>X</math>. Hence, | ||
Latest revision as of 13:17, 6 March 2021
When we work with multiple information sources (random variables) and , the following details are useful:
- How much information overlap is there between and ?
- How much information is contained in one but not present in the other?
In information theory, we formalize the first question using the concept of mutual information, while the second question is addressed using the concept of conditional entropy.
Contents
Definition
For two random variables and , the mutual information between them, denoted by is given by
,
and the conditional entropy of given is given by
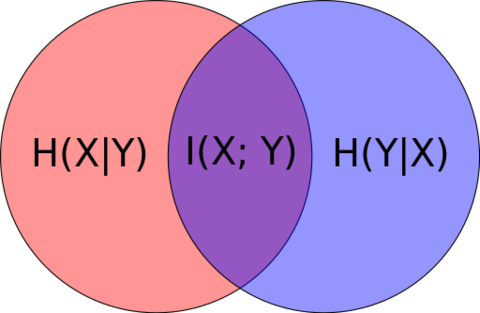
Observe that the fraction in the definition of consists of (1) the joint distribution , and (2) the product of marginal distributions . is a measure of how far and is from being independent, in which case and the entire summation vanishes since . In our discussions, we simplify the notation so that and both refer to the probability that . With this remark, . However, conditional entropy is not symmetric, i.e. in general is not equal to .
When and are independent, all conditional probabilities reduces to , i.e., conditioning on does not change the probability of . Hence,
Thus, if and are independent.
Even if we do not require and to be independent, rearranging terms reveals yet another intuitive property.
The summation inside the parenthesis should be very familiar. Indeed, if we ignore the conditioning on , we see that the summation is essentially a calculation of entropy. Together with the , is simply a weighted average of multiple entropy values! For a detailed discussion of this property with numerical example, please see Activity 2.
Entropy, conditional entropy, and mutual information
Below are some properties that relate all information measures we discussed so far (entropy, conditional entropy, mutual information):
- where equality holds if and only if and are independent.
- For all random variables and ,
The first property is crucial in understanding the implications of mutual information. Wherever occurs in important properties, it would greatly help to check if a property with still makes sense, knowing that and would be independent under such constraint.
In many cases, however, would be strictly positive. The second property then implies that in many cases, would be strictly less than , i.e., conditioning reduces entropy, and is precisely the amount of reduction in entropy/information about when we know .
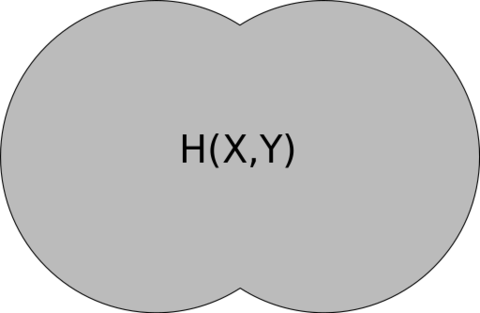
The Venn diagram shown below serves as a visual aid to remember the relationships between entropy, conditional entropy and mutual information.
Extensions
What happens when we deal with more than two random variables? To facilitate the discussion, let us recall the chain rule for joint distributions.
Let be a sequence of discrete random variables. Then, their joint distribution can be factored as follows
,
Chain rule for entropy
The chain rule for (joint) entropy is very similar to the above expansion, but we use additions instead of multiplications.
Although we do not supply a complete proof here, this fact should not be too surprising since entropy operates on logarithms of probabilities and logarithms of product terms expand to sums of logarithms.
Proof of chain rule for
Let us see that the statement is true for . Let be three discrete random variables. The idea with the proof is that we operate on two random variables at a time, since prior to the chain rule we only know that . We can write , where we bundle and into one random variable .
The proof now proceeds as follows:
One interpretation of the chain rule shown is that to obtain the total information (joint entropy) of as a whole, we can
- obtain information about first without any prior knowledge: , then
- obtain information about with knowledge of : , then
- obtain information about with knowledge of and : .
For , we can proceed by induction. Below is the sketch of the proof:
- (Base step) For a fixed n=k, assume that any collection of random variables satisfies the chain rule.
- (Induction step) When n = k+1, write the joint entropy of rvs as follows: , where the first are bundled together into one random variable.
- Use the two-variable chain rule and the base step to show that .





































![{\displaystyle H(X_{1},X_{2},X_{3})=H((X_{1},X_{2}),X_{3})=H(X_{1},X_{2})+H(X_{3}|X_{1},X_{2})=[H(X_{1})+H(X_{2}|X_{1})]+H(X_{3}|X_{1},X_{2})}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/1e814d88da43a98bed63adf8f11bc71e815d00c0)










